GAN 的后序
参考资料
网络博客
令人拍案叫绝的Wasserstein GAN - 知乎 (zhihu.com)
生成式对抗网络GAN有哪些最新的发展,可以实际应用到哪些场景中? - 知乎 (zhihu.com)
从动力学角度看优化算法:GAN的第三个阶段 - 知乎 (zhihu.com)
视频讲解
Lecture 6 对抗生成网络GAN(2018) Wasserstein GAN(WGAN) 和 Energy-based GAN(EBGAN)_哔哩哔哩_bilibili
李宏毅对抗生成网络(GAN)国语教程(2018)_哔哩哔哩_bilibili
相关论文:
Least Squares GAN LSGAN
使用 线性函数代替 Sigmoid , 解决梯度消失的问题
Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks DCGAN
依靠的是对判别器和生成器的架构进行实验枚举,最终找到一组比较好的网络架构设置,但是实际上是治标不治本,没有彻底解决问题
| [TOWARDS PRINCIPLED METHODS FOR TRAINING GENERATIVE ADVERSARIAL NETWORKS]([Towards Principled Methods for Training Generative Adversarial Networks | Papers With Code](https://paperswithcode.com/paper/towards-principled-methods-for-training)) |
从理论上分析了原始GAN的问题所在,从而针对性地给出了改进要点。
并针对第二点提出了一个解决方案,就是对生成样本和真实样本加噪声,直观上说,使得原本的两个低维流形“弥散”到整个高维空间,强行让它们产生不可忽略的重叠。而一旦存在重叠,JS散度就能真正发挥作用,此时如果两个分布越靠近,它们“弥散”出来的部分重叠得越多,JS散度也会越小而不会一直是一个常数,于是(在第一种原始GAN形式下)梯度消失的问题就解决了。在训练过程中,我们可以对所加的噪声进行退火(annealing),慢慢减小其方差,到后面两个低维流形“本体”都已经有重叠时,就算把噪声完全拿掉,JS散度也能照样发挥作用,继续产生有意义的梯度把两个低维流形拉近,直到它们接近完全重合。以上是对原文的直观解释。
Wasserstein GAN WGAN
成功地做到了以下爆炸性的几点:
- 彻底解决GAN训练不稳定的问题,不再需要小心平衡生成器和判别器的训练程度
- 基本解决了collapse mode的问题,确保了生成样本的多样性
- 训练过程中终于有一个像交叉熵、准确率这样的数值(Wasserstein 距离)来指示训练的进程,这个数值越小代表GAN训练得越好,代表生成器产生的图像质量越高
- 以上一切好处不需要精心设计的网络架构,最简单的多层全连接网络就可以做到
从这个改进点出发推了一堆公式定理,最终给出了改进的算法实现流程,而改进后相比原始GAN的算法实现流程却只改了四点:
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行
Improved Training of Wasserstein GANs
WGAN存在着训练困难、收敛速度慢等问题。其实,WGAN的作者Martin Arjovsky不久后就在reddit上表示他也意识到了这个问题,认为关键在于原设计中Lipschitz限制的施加方式不对,并在新论文中提出了相应的改进方案WGAN-GP:显著提高了训练速度,解决了原始WGAN收敛缓慢的问题
生成对抗网络的应用
生成对抗网络(GAN)的18个绝妙应用 - 云+社区 - 腾讯云 (tencent.com)
热搜第一!B站up主用AI让李大钊陈延年等露出了笑容,人民日报:如今的中国,已如你们所愿! - 知乎 (zhihu.com)
【AI修复】我用人工智能修复了100年前的北京影像!!【1920年】【60FPS彩色】【大谷纽约实验室】_哔哩哔哩_bilibili
GAN存在的问题
原始GAN问题的根源可以归结为两点,一是等价优化的距离衡量(KL散度、JS散度)不合理,二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠。
1 在实际中,任何两个manifolds都不会perfectly align.
首先是,为什么生成样本和真实样本很难有不可忽略的重叠部分?

但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略,
理解:
GAN中的生成器一般是从某个低维(比如100维)的随机分布中采样出一个编码向量,再经过一个神经网络生成出一个高维样本(比如64x64的图片就有4096维)。当生成器的参数固定时,生成样本的概率分布虽然是定义在4096维的空间上,但它本身所有可能产生的变化已经被那个100维的随机分布限定了,其本质维度就是100,再考虑到神经网络带来的映射降维,最终可能比100还小,所以生成样本分布的支撑集就在4096维空间中构成一个最多100维的低维流形,“撑不满”整个高维空间。
“撑不满”就会导致真实分布与生成分布难以“碰到面”,这很容易在二维空间中理解:一方面,二维平面中随机取两条曲线,它们之间刚好存在重叠线段的概率为0;另一方面,虽然它们很大可能会存在交叉点,但是相比于两条曲线而言,交叉点比曲线低一个维度,长度(测度)为0,可忽略。三维空间中也是类似的,随机取两个曲面,它们之间最多就是比较有可能存在交叉线,但是交叉线比曲面低一个维度,面积(测度)是0,可忽略。
从低维空间拓展到高维空间,就有了如下逻辑:因为一开始生成器随机初始化,所以几乎不可能与
有什么关联,所以它们的支撑集之间的重叠部分要么不存在,要么就比
和
的最小维度还要低至少一个维度,故而测度为0。
另一个理解:即使存在重叠,但是我们是一个取样的过程,所以会出现即使出现重叠,但并不能充分表现出来
2 JS散度的问题
第二个问题是 JS散度的不合理性。
JS散度是无法刻画不重合的分布之间的距离的。如下图所示,当不重合的时候对于JS散度来说结果都是一样的,也就是说JS散度是无法刻画的。
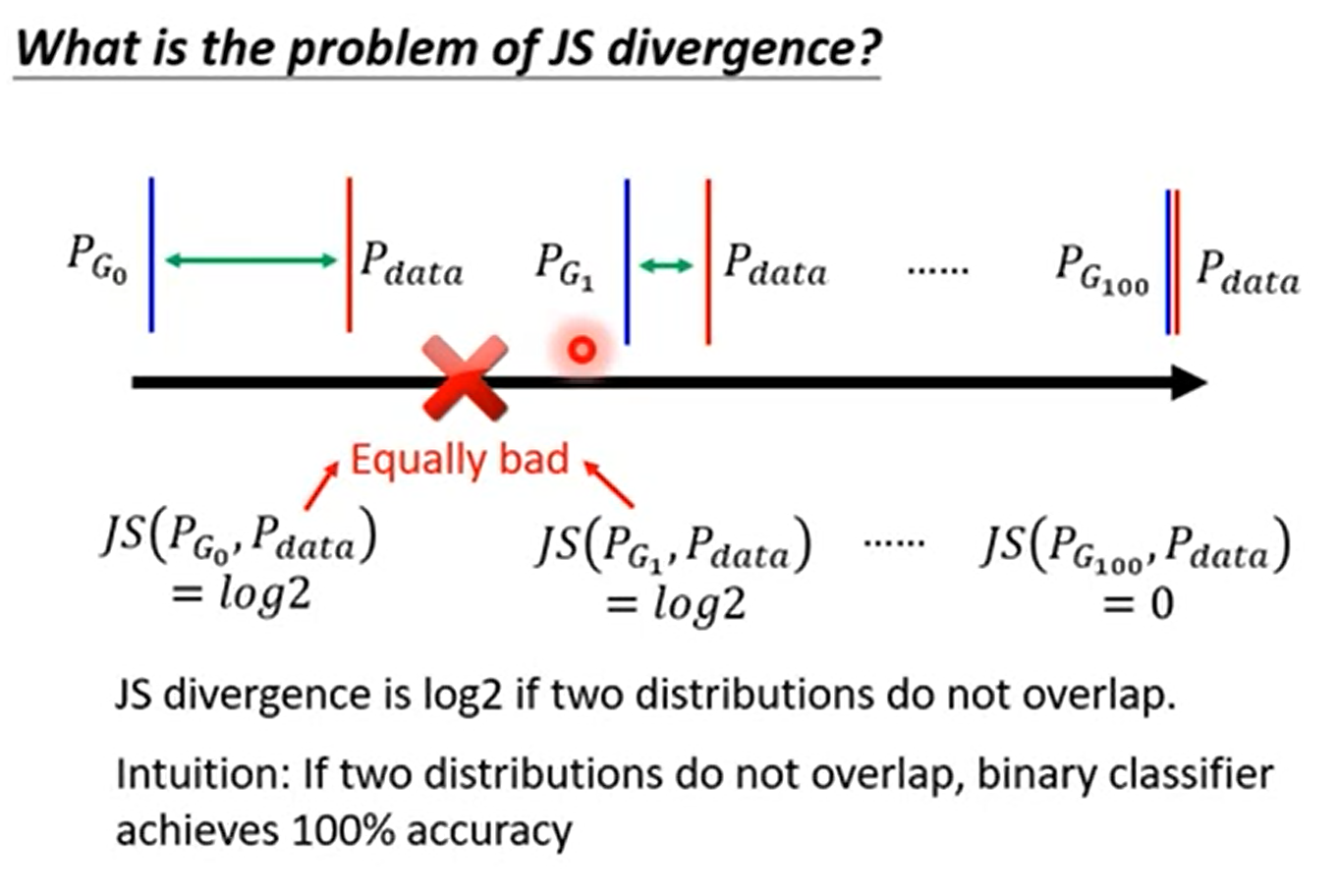
改进1 LeastSquareGAN
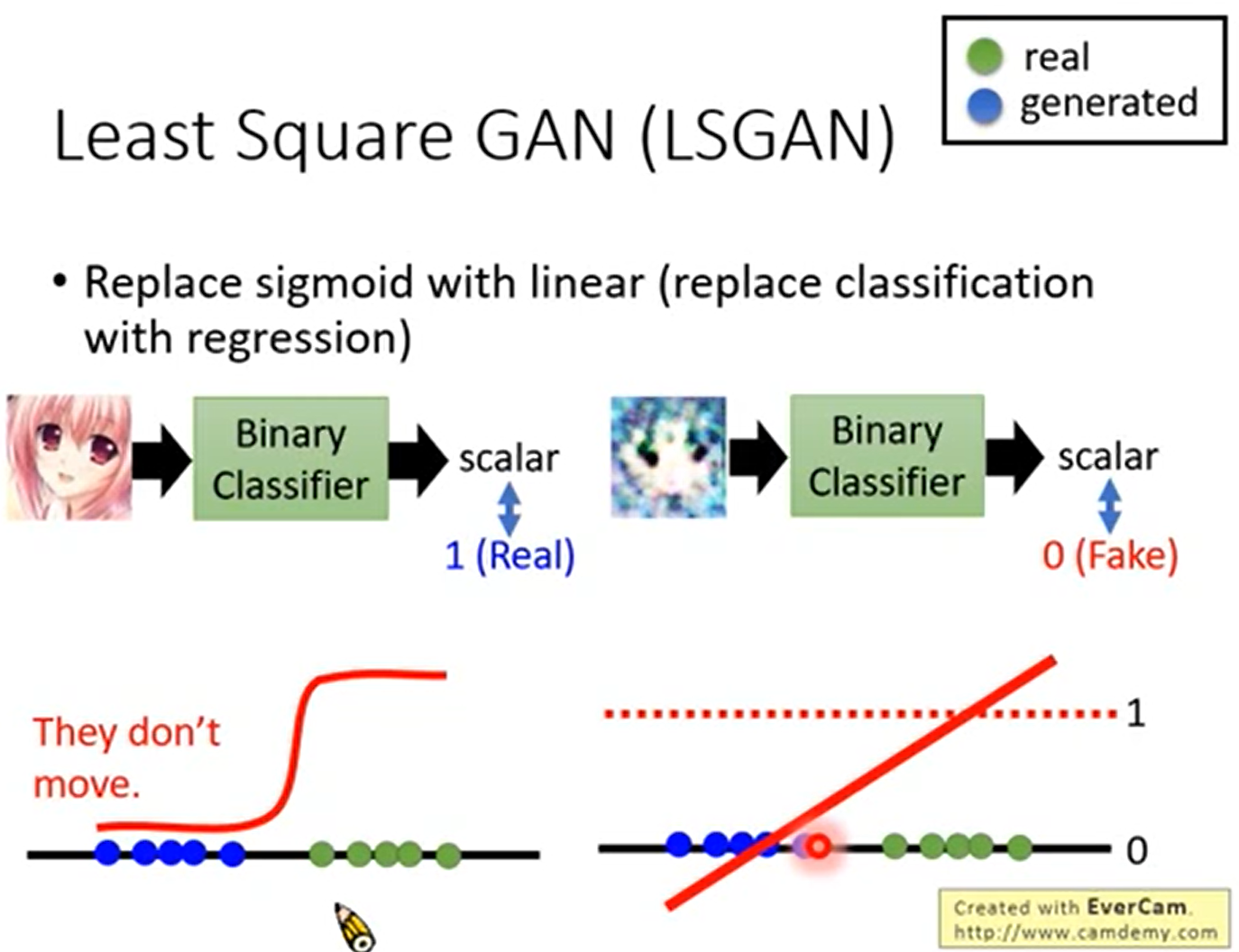
鉴别器做的实际是一个二分类问题,判别函数就是Sigmoid函数,但是我们从Sigmoid函数可以看出,当鉴别器具有很好的分类效果时,对应图像的梯度几乎为0,也就是出现了梯度消失的问题。
LSGAN就用线性函数代替Sigmoid函数,将一个分类问题变成了一个拟合问题,根据拟合的结果对样本进行分类。
改进2 WGAN
使用Wassersetin Distance 来衡量两个分布的差异
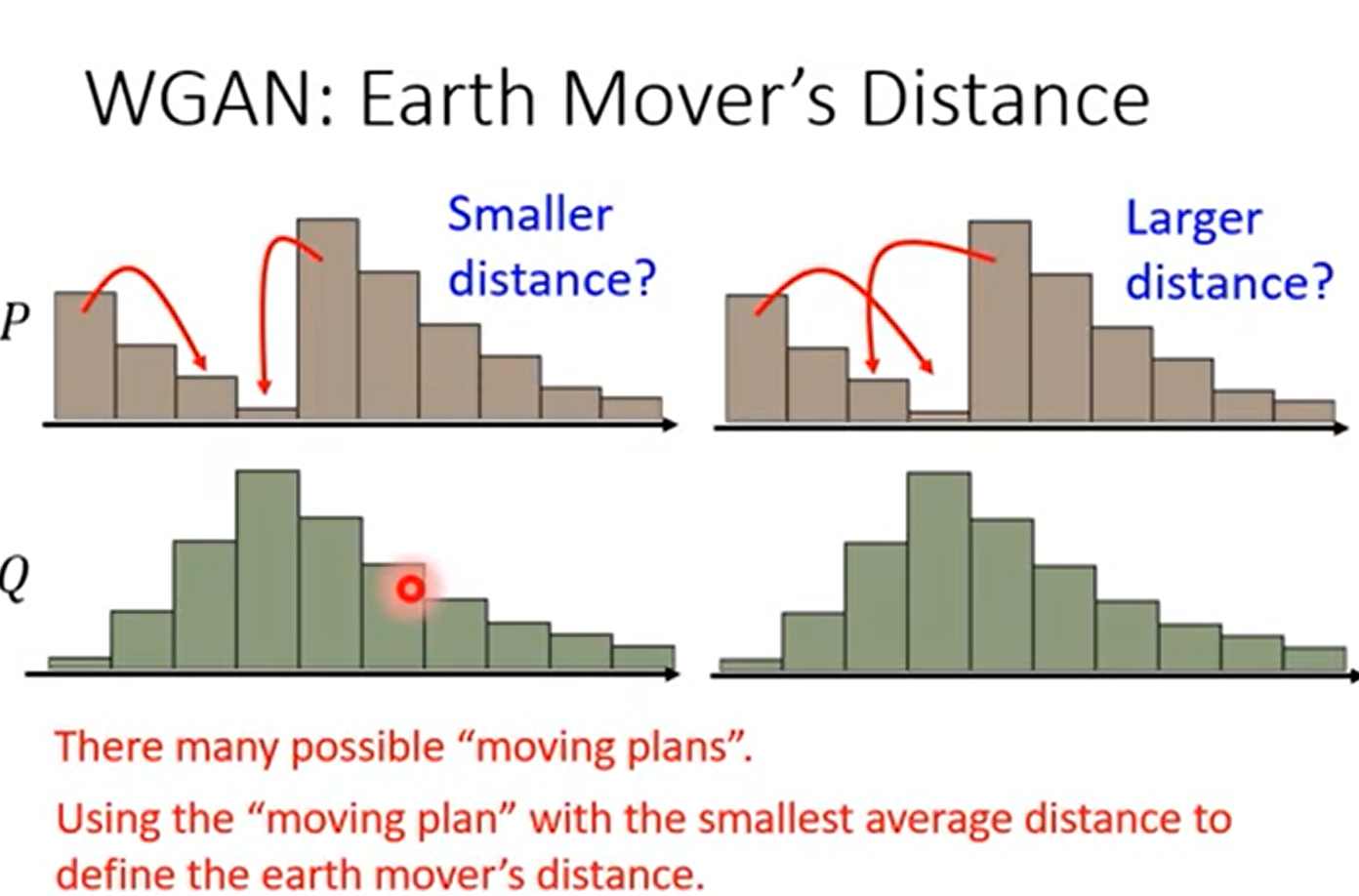
介绍 推土机距离 EarthMove Distance1
Lecture 6 对抗生成网络GAN(2018) Wasserstein GAN(WGAN) 和 Energy-based GAN(EBGAN)_哔哩哔哩_bilibili 18:12

在一维分布时,很形象
但在二维上面,事实上有很多种方法,推土机距离就是定义为穷举所有的方案,距离最小的哪个
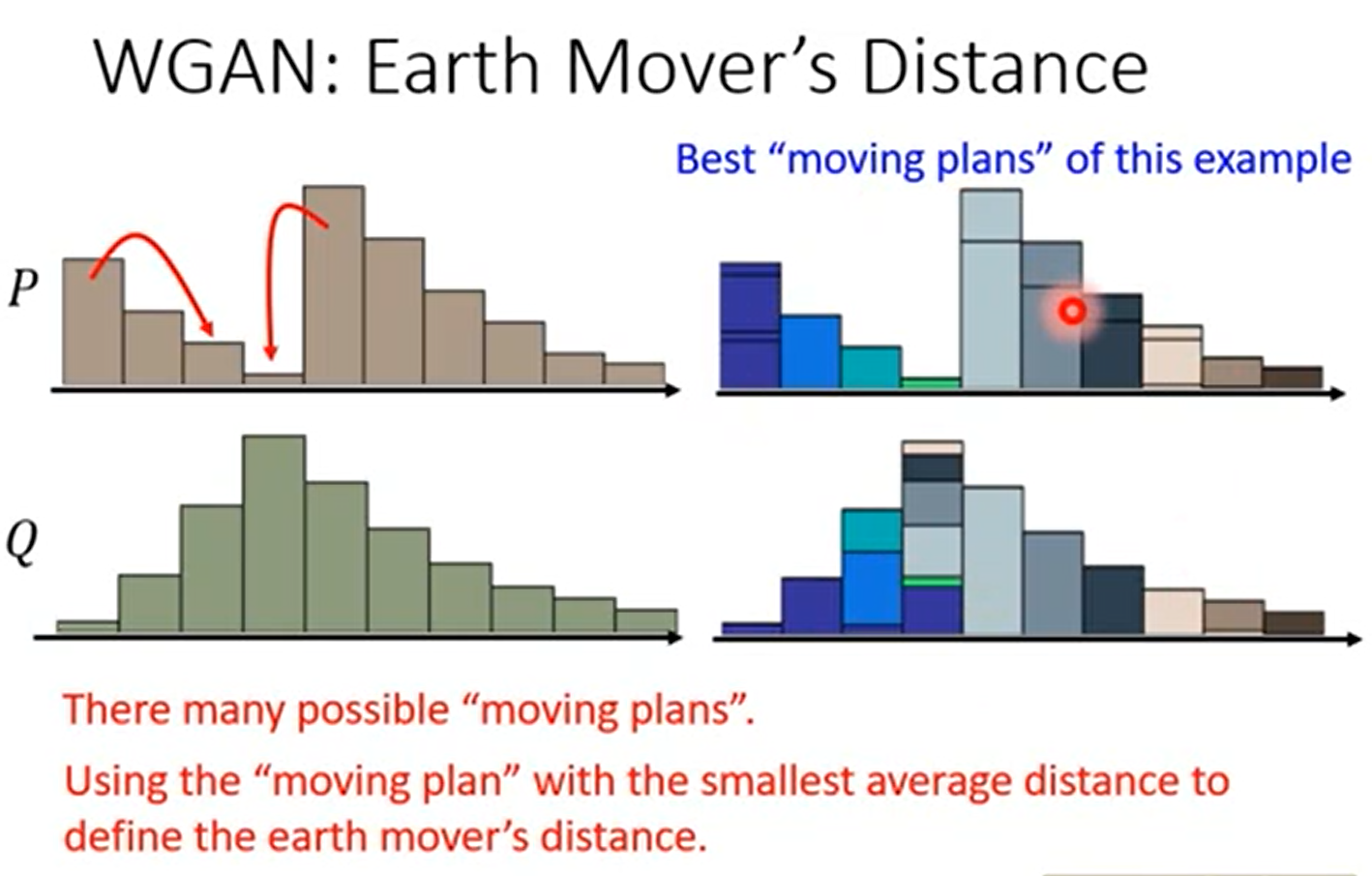
正式定义
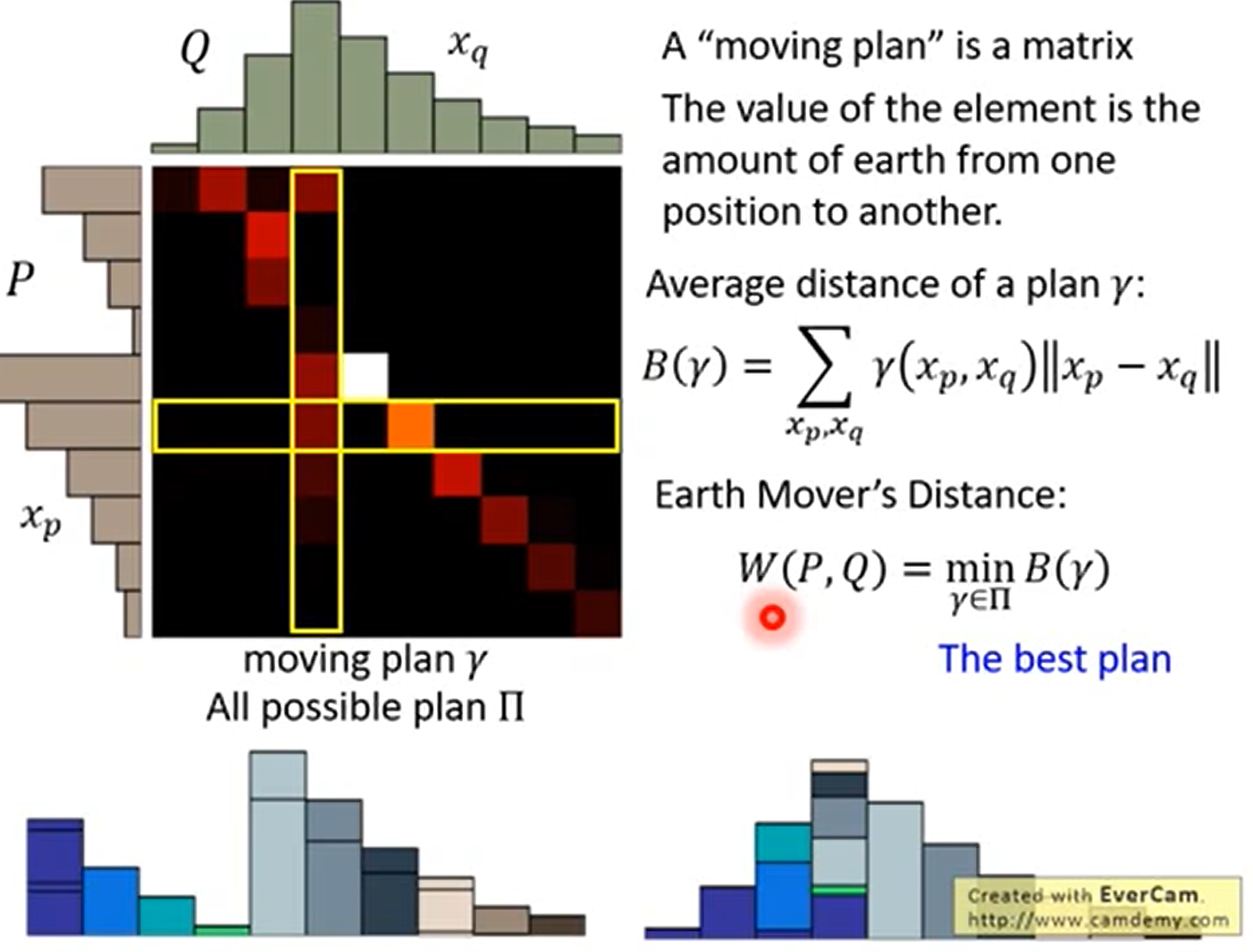
Earth Mover’s Distance 的优点
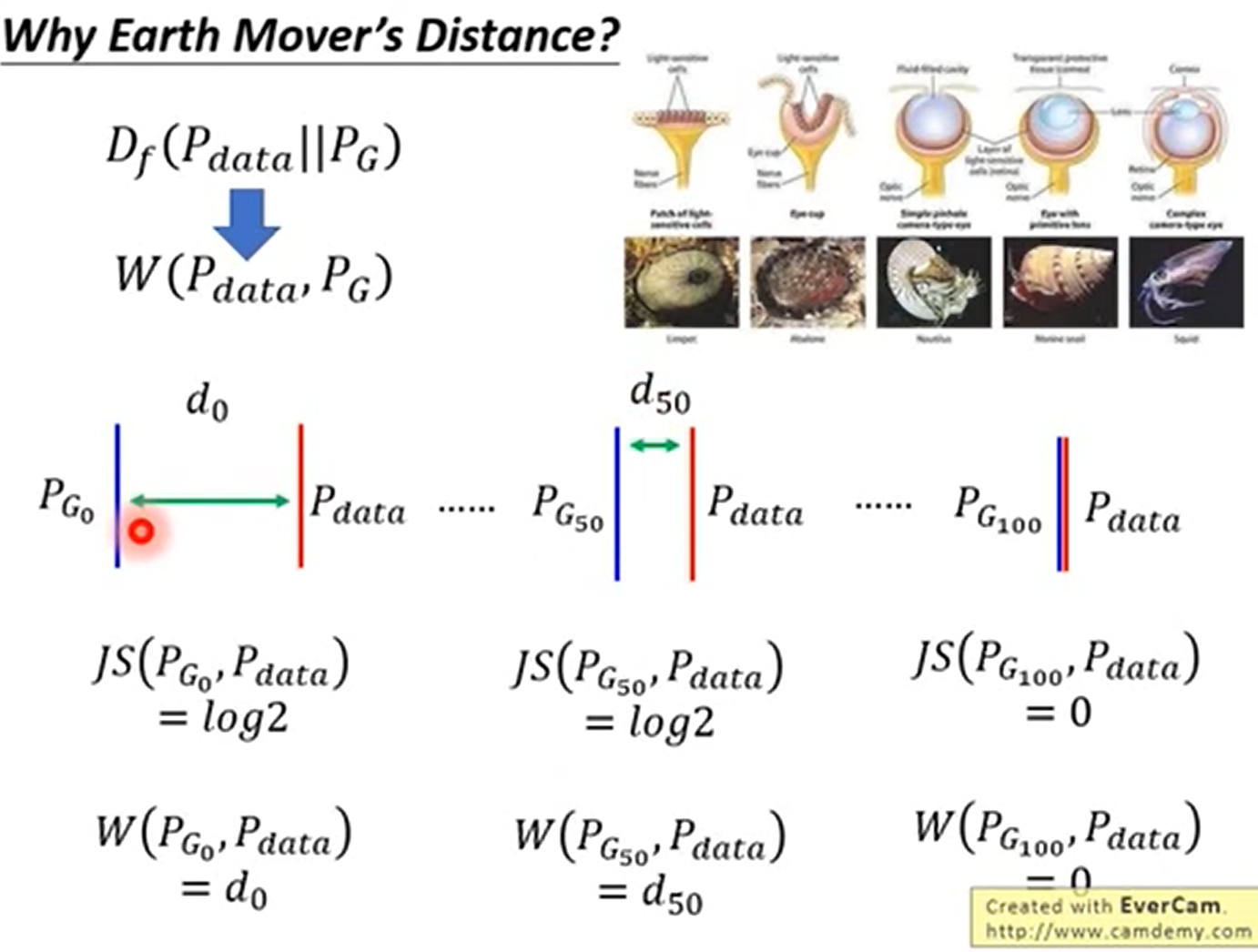
能够衡量不相交的时候的距离,并且距离越近效果越好
WGAN 使用 Wassterstein

$D \in 1-Lipschitz$就是要包证收敛
给出 Lipschitz Function 含义

在原始的WGAN中为了保持1-lipschitz,使用Weight Clipping只是给出了范围限制。但是这样并没有解决这个问题
在后序的Improved WGAN(WGAN-GP)中,使用显示样本的梯度效小于1来解决1-lipschitz的问题

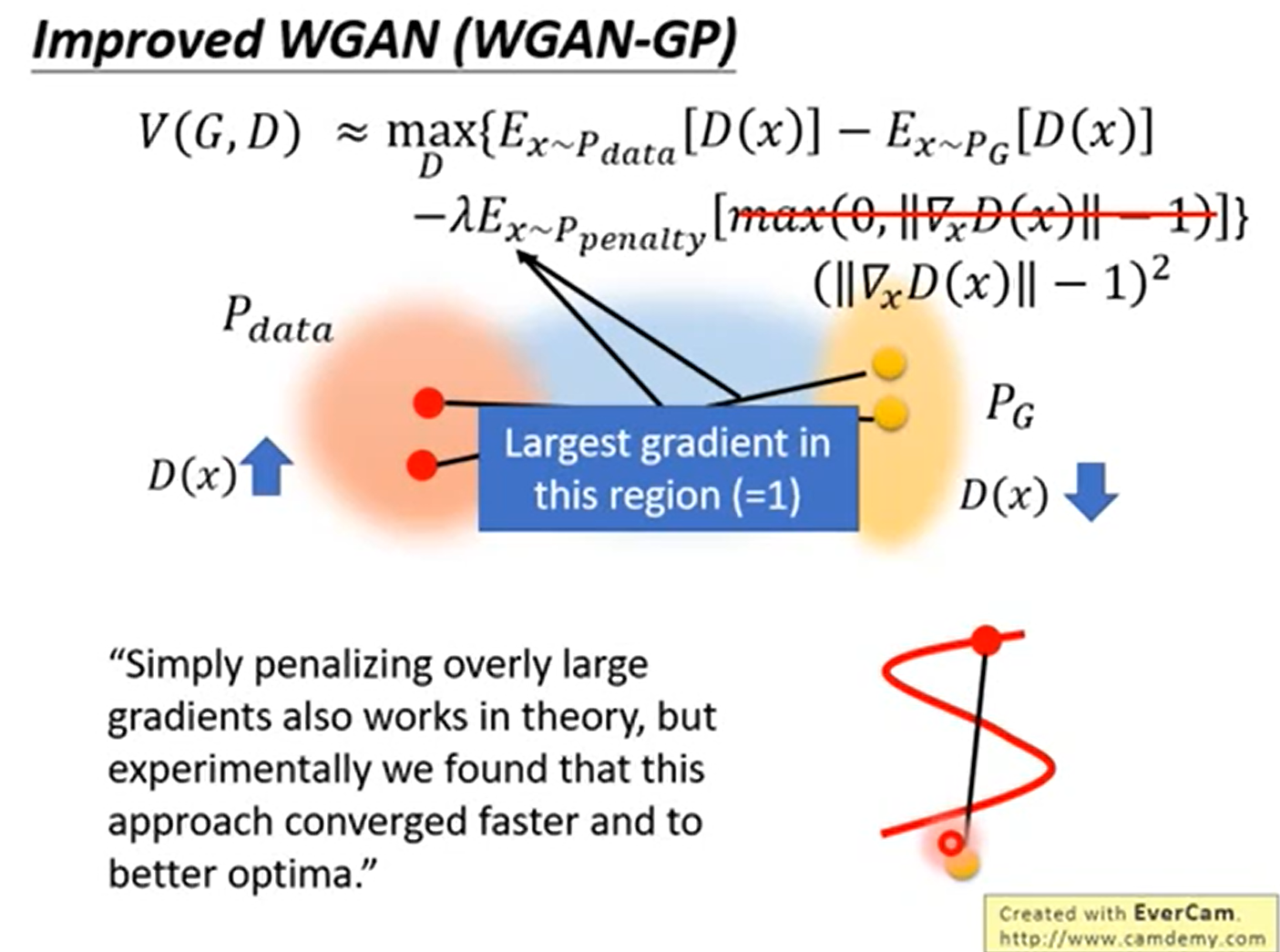
还是有问题的,按着WGP
DragonGAN
改进3 Spectrum Norm

从GAN到WGAN算法的改进
而改进后相比原始GAN的算法实现流程却只改了四点:
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行

改进4 Energy-based GAN (EBGAN)
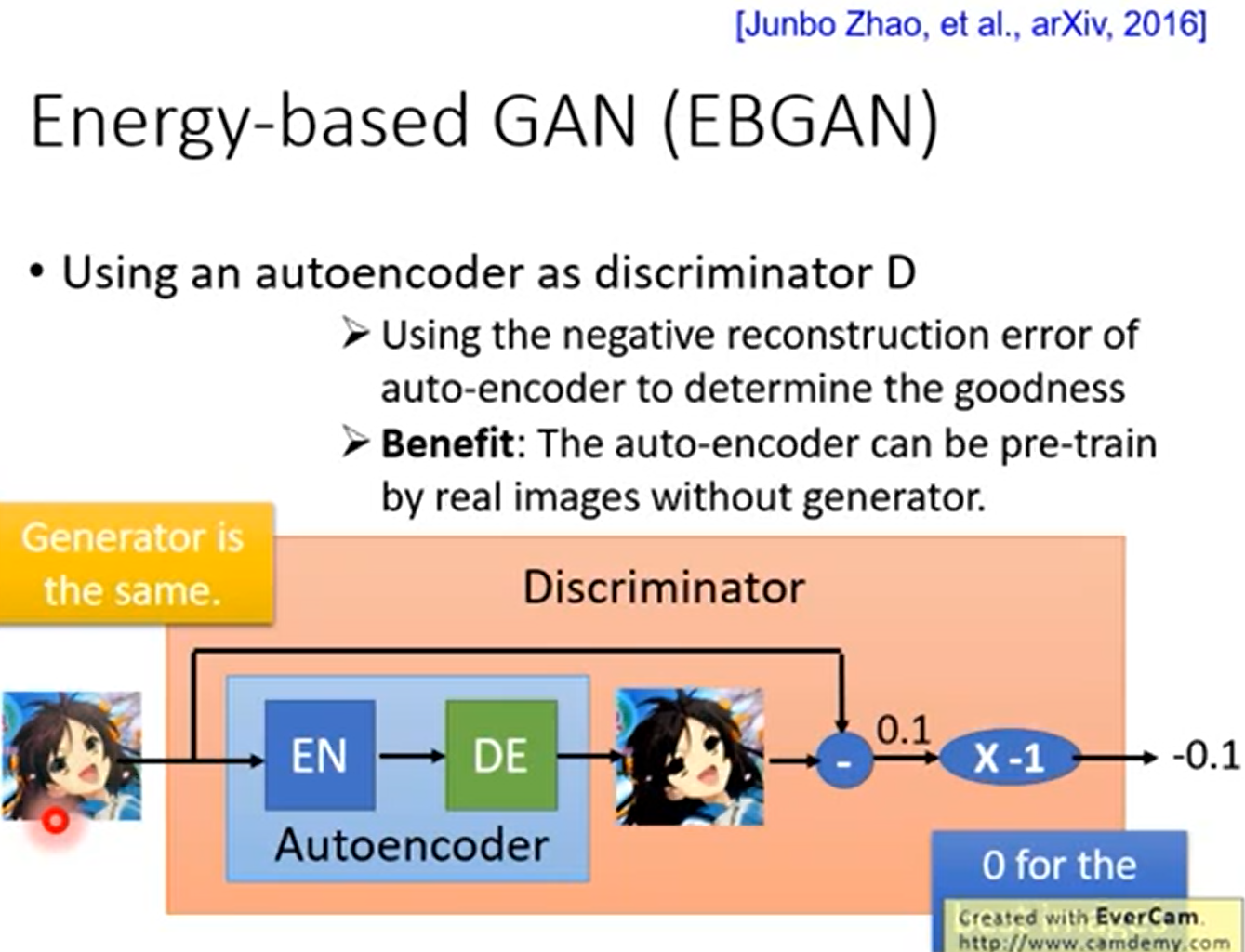
鉴别器不需要等生成器生成较好的
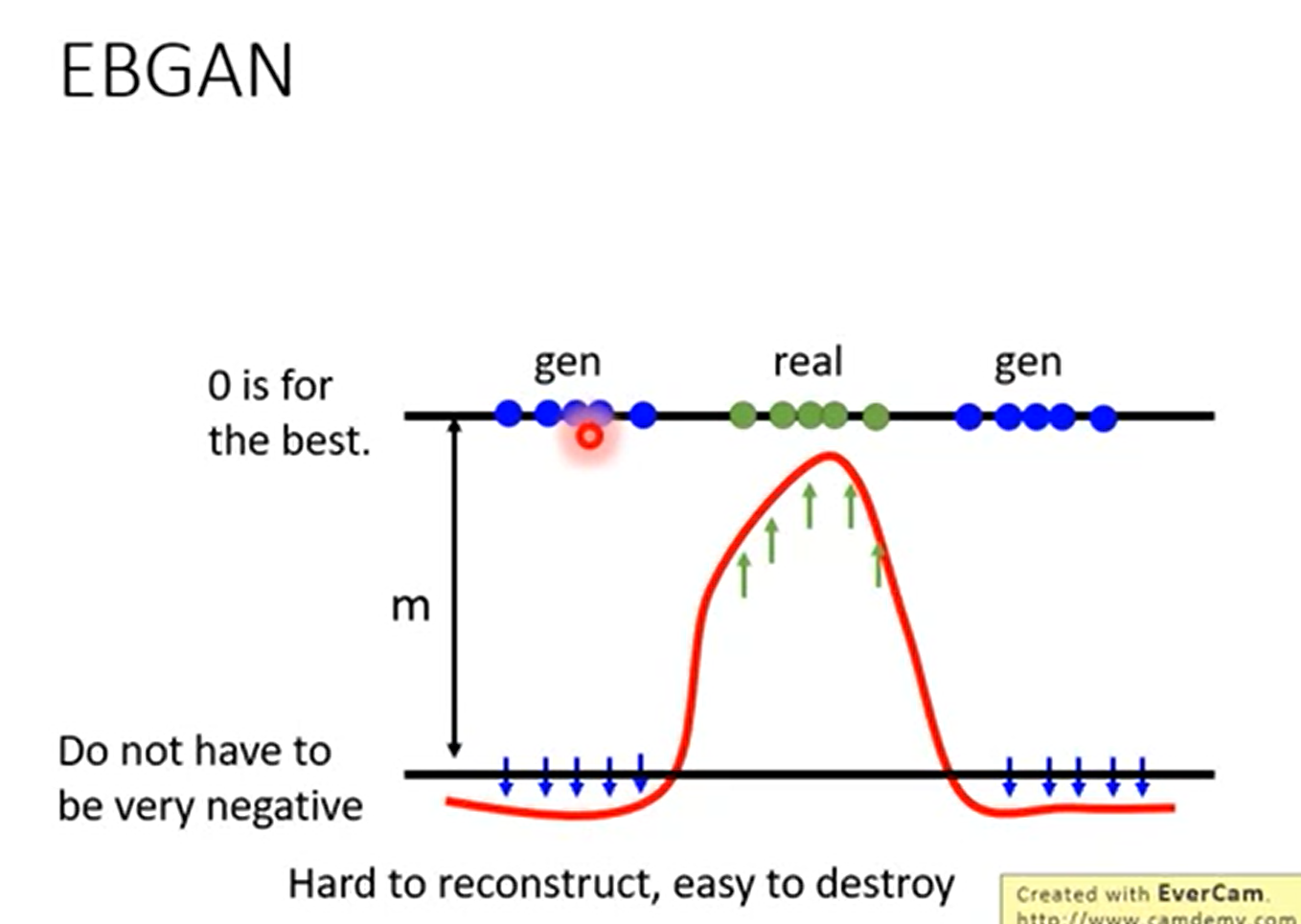
改进5 Loss-Sensitive GAN
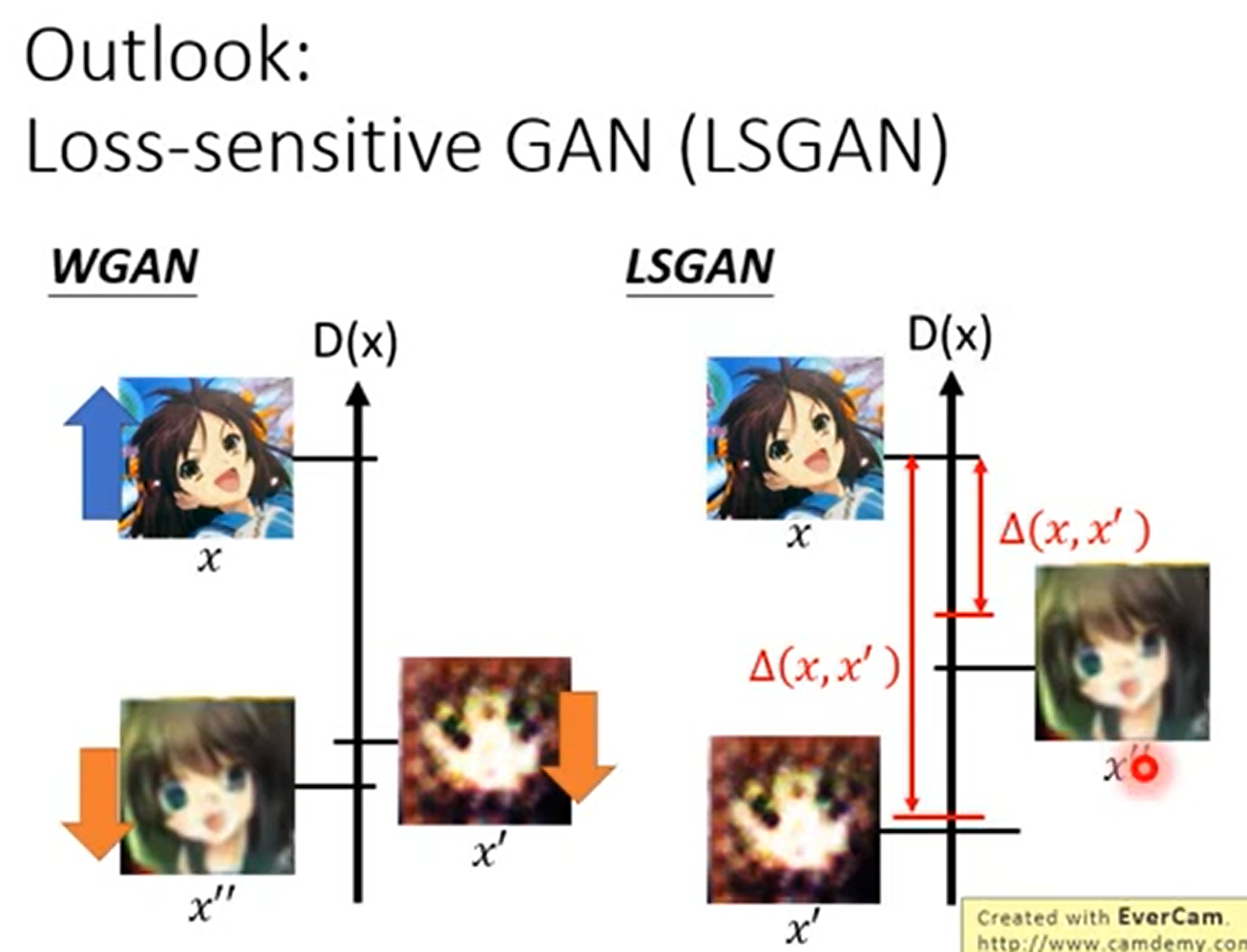
Wasserstein GAN


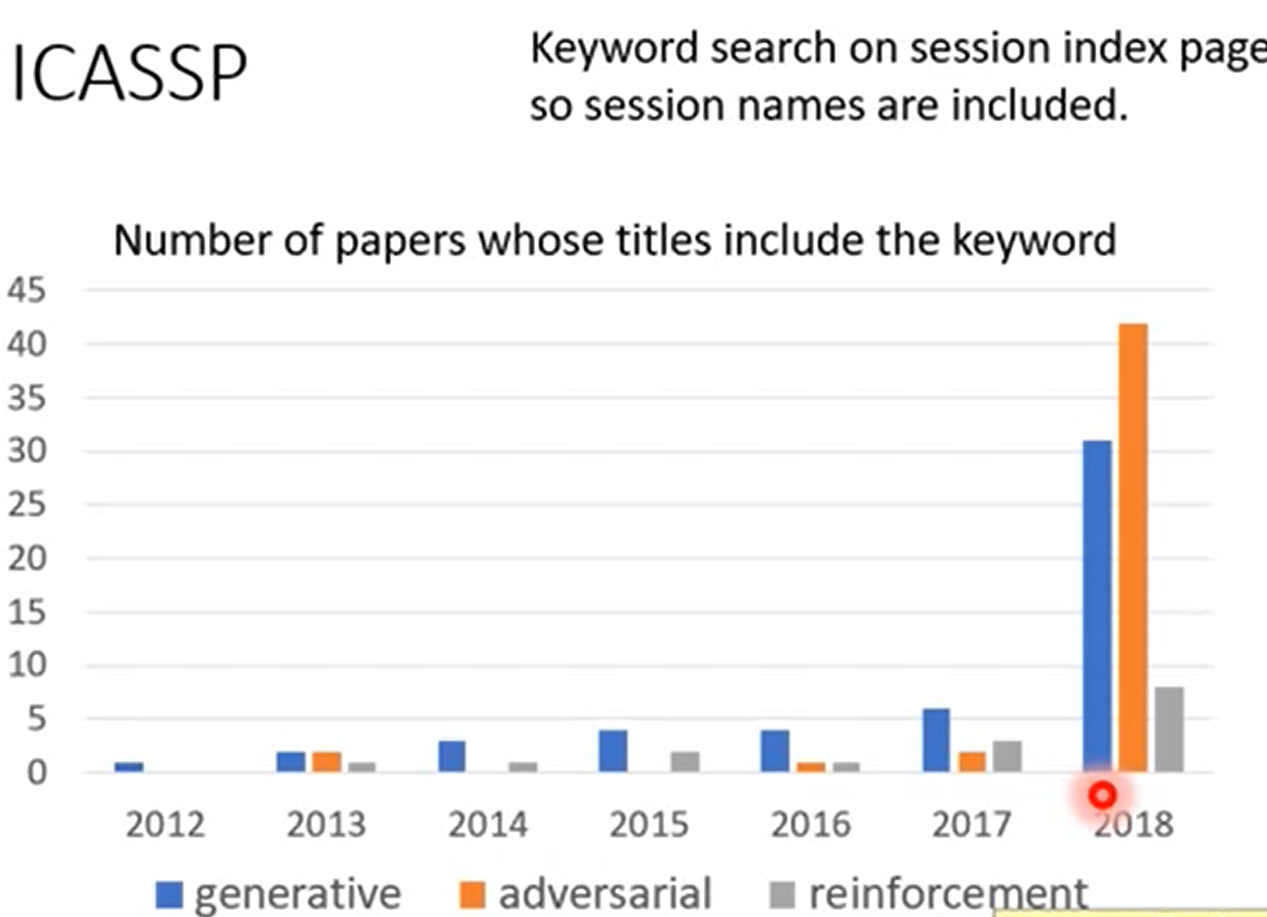
精读论文
1 TOWARDS PRINCIPLED METHODS FOR TRAINING GENERATIVE ADVERSARIAL NETWORKS
标题 作者 期刊


作者 Martin Arjovsky
Abstract
1 Introduction
2 Sources of Instability
GAN算法的理论和实际使用时效果不一致,给出了背后原因在于 the distributions are not continuous 或者 they have disjoint supports ,后面给出了理论的分析与证明,最终结论就是 This shows that as our discriminator gets better, the gradient of the generator vanishes.
为什么JS散度不合理呢?就是因为1 实际上两个分布没有很多重合的地方。2,即使有,那我们的取样过程也会导致pg和pdata没有重合的地方。

当没有重合的时候,结果就是Log2 梯度为0。
实际上,只要不重合,对于JS来说
3 TOWARDS SOFTER METRICS AND DISTRIBUTIONS
针对第二点提出了一个解决方案,就是对生成样本和真实样本加噪声,直观上说,使得原本的两个低维流形“弥散”到整个高维空间,强行让它们产生不可忽略的重叠。而一旦存在重叠,JS散度就能真正发挥作用,此时如果两个分布越靠近,它们“弥散”出来的部分重叠得越多,JS散度也会越小而不会一直是一个常数,于是(在第一种原始GAN形式下)梯度消失的问题就解决了。在训练过程中,我们可以对所加的噪声进行退火(annealing),慢慢减小其方差,到后面两个低维流形“本体”都已经有重叠时,就算把噪声完全拿掉,JS散度也能照样发挥作用,继续产生有意义的梯度把两个低维流形拉近,直到它们接近完全重合。以上是对原文的直观解释。
2 Wasserstein GAN
标题 作者 期刊

Abstract
1 Introduction
2 Different Distace
3 Wasserstein GAN
我们来对比一下 WGAN和 GAN的算法流程

4 Empirical Results
5Related Work
6 Conclusion
3 Improved Training of Wasserstein GANs
标题 作者 期刊

Abstract
1 Introduction
2 Background
2.1 Generative adversarial networks
2.2 Wasserstein GANs
2.3 Properties of the optimal WGAN critic
3 Difficulties with weight constraints
3.1 Capacity underuse
3.2 Exploding and vanishing gradients
4 Gradient penalty
5 Experiments
6 Conclusion
GAN 后续研究方向

GAN的发展
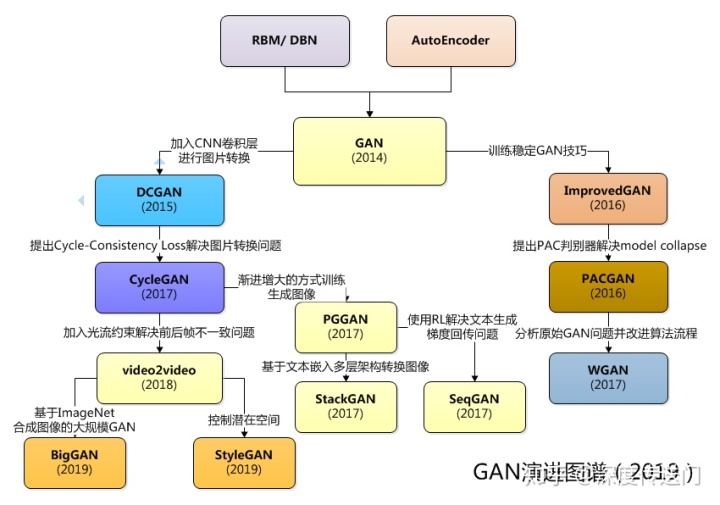
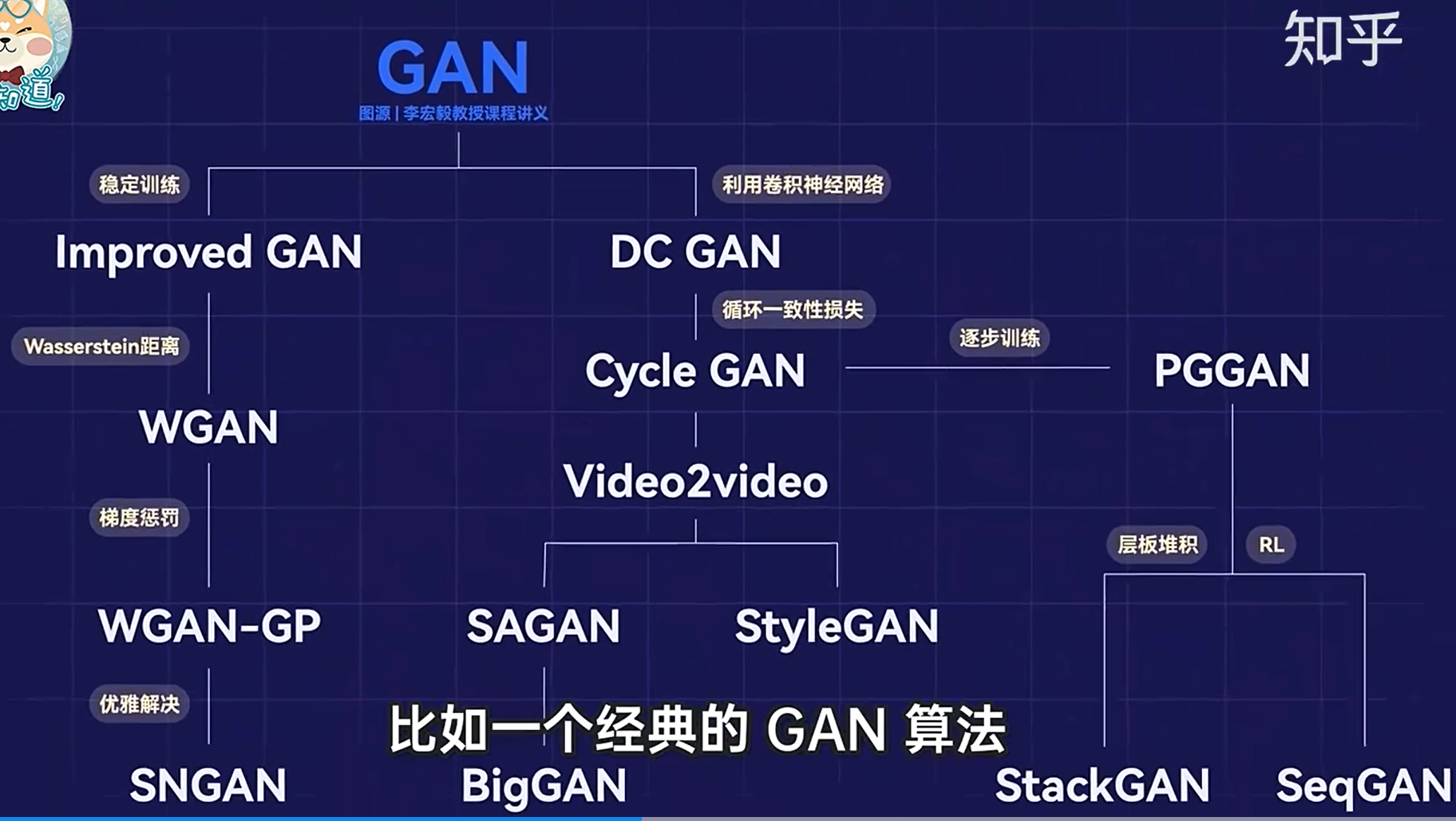
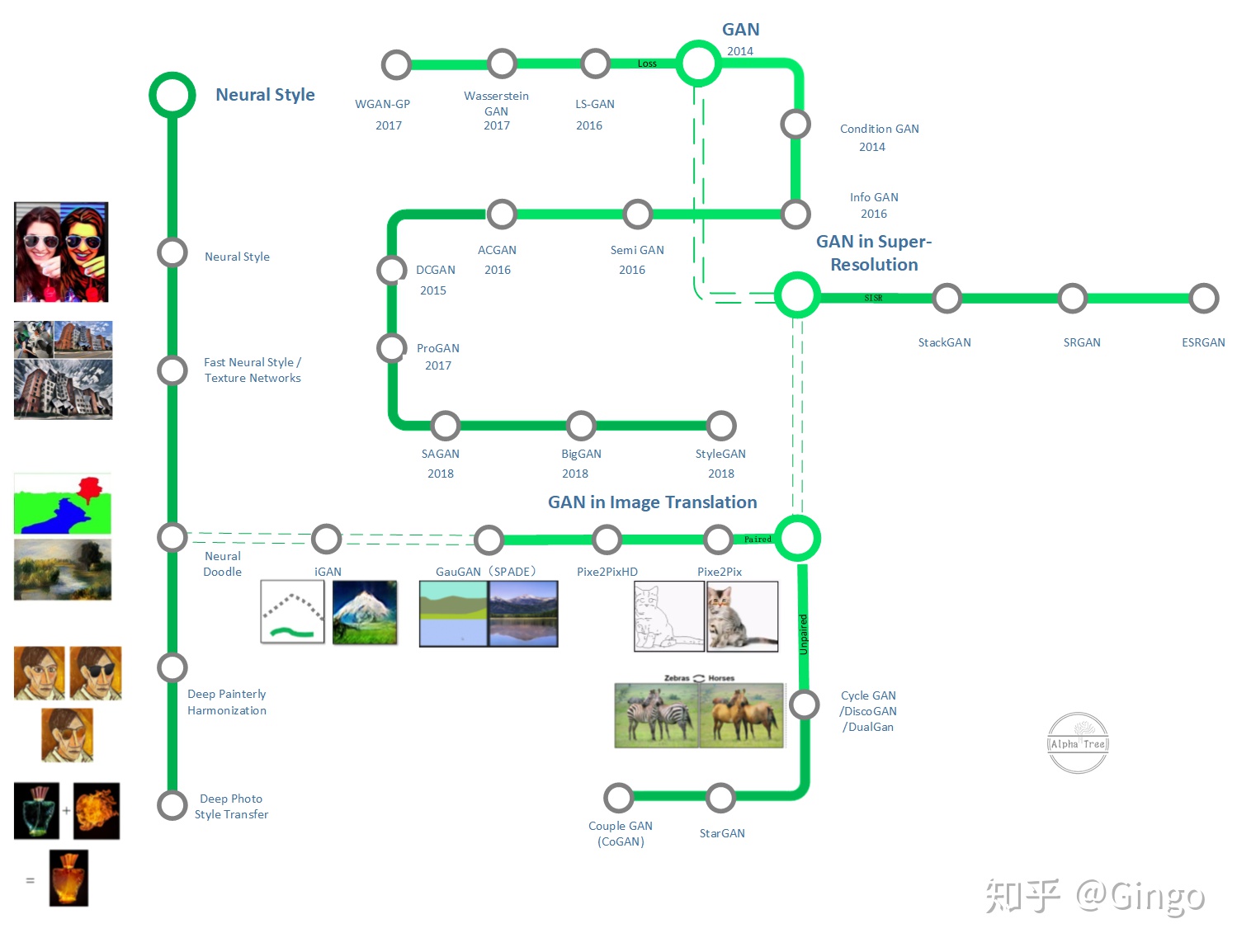
文档信息
- 本文作者:zuti666
- 本文链接:https://zuti666.github.io/2021/11/16/Development-of-GAN/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)