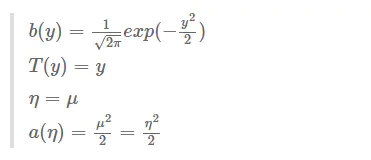广义线性模型GLM

判断标准非常简单，响应变量y独立则GLM，否则GLMM。这就是最本质的判断标准，其它的标准都是基于这个标准来的

指数分布族

总体$X$概率密度为 \(f_X(x;\theta) = h(x) e^{ (\ \eta(\theta)\cdot T(x)+A(\theta)\ )}\)

其中

$\eta(\theta)$​​​​​​被称为这个分布的自然参数(natural parameter )

$T(x)$​​​​​​​为充分统计量(sufficient statistic) ，通常 $T(x)=x$​​​​​

$A(\theta)$​​​​​​为累计函数(cumulant function) ， 作用是确保概率和$\sum f(x;\theta)$​​​​为1

$h(x)$​​​为 underlying measure

当 $T,A,h(y)$​​​固定之后就确定了指数分布族中的一种分布模型，就得到了以$\eta$​​​为参数的模型

还有两个等价的形式 \(f_X(x|\theta) = h(x) g(\theta) e^{(\ \eta(\theta)\cdot T(x) \ )} \\ f_X(x|\theta) = e^{(\ \eta(\theta)\cdot T(x)+ A(\theta) \ )}\)

设总体$X$的分布密度为$f(x:\mathbfcal{\theta})$，其中$\mathbfcal{\theta}=(\theta_1,\theta_2,\dots,\theta_n)^T$

$(X_1,X_2,\dots,X_n)^T$为其样本，若样本的联合分布密度具有形式 \(\prod_{i=1}^n f(x,\mathbfcal{\theta})= C(\mathbfcal{\theta}) exp\{\sum_{j=1}^mb_j(\mathbfcal{\theta}) T_j(x_1,x_2,\cdots,x_n) h(x_1,x_2,\cdots,x_n) \}\) 并且集合${x:f(x;\mathbfcal{\theta} )>0}$不依赖于$\mathbfcal{\theta}$。

• 其中$C(\mathbfcal{\theta}),b_j(\mathbfcal{\theta})$只与参数$\mathbfcal{\theta}$有关而与样本无关
• $T_j,h$只与样本有关而与参数$\mathbfcal{\theta}$无关

则称集合${f(x;\mathbfcal{\theta} ): \mathbfcal{\theta} \in \Theta}$为指数分布族

其实，大多数概率分布都属于指数分布族：

• 伯努利分布（Bernouli）：对0,1问题进行建模
• 二项分布(Multinomial): 对K个离散结果的事件建模
• 泊松分布(Poisson)
• 指数分布(exponential)和伽马分布(gamma)：
• 高斯分布(Gaussian)
• $\cdots$

指数分布族中常用的分布

求解的方法就是将概率分布符合指数分布族的转换成它对应的指数分布族的形式，求出指数分布族对应位置上的参数即可求出原模型的参数。

伯努利分布 Bernoulli

伯努利分布是假设一个事件只有发生或者不发生两种可能，并且这两种可能是固定不变的。那么，如果假设它发生的概率是 p，那么它不发生的概率就是 1-p。这就是伯努利分布。

伯努利实验就是做一次服从伯努利概率分布的事件，它发生的可能性是 p，不发生的可能性是 1-p。

$X$	$1$	$0$
$P$	$p$	$1-p$

\[f(x|p)=p^xq^{1-x}\]

我们来通过对伯努利的分布函数进行变形来展示伯努利分布是指数分布族中的一员 $$ \begin{aligned} P(x; p) &= p^x(1-p)^{(1-x)}
&= e^{log p^x} \cdot e^{log(1-p)^{1-x}}
&=e^{xlog p+(1-x)log(1-p)}
&=e^{xlog\frac{p}{1-p}+log(1-p)}

\end{aligned} $$ 这就和$f_X(x;\theta) = h(x) e^{ (\ \eta(\theta)\cdot T(x)+A(\theta)\ )}$的形式归为一致了

也就是说，我们选择

• $\eta (\theta)=log\frac{p}{1-p}$作为自然参数

• $T(x)=x$
• $A(\theta)=log(1-p)=log(1+e^\eta(p))$
• $h(x)=1$​​

时，指数分布族就是伯努利分布

泊松分布 Poisson

泊松分布的概率函数为 \(P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda},k=0,1\cdots\) 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

因此，泊松分布也属于指数分布族，其相关参数为

• $\eta({\theta} )= log \lambda $
• $T(x)=x$
• $A(\theta) = \lambda = e^\eta$​
• $h(x)=\frac{1}{x!}$

高斯分布(正态分布) Gaussian

单高斯分布的公式 \(p(x;\mu,\delta) = \frac{1}{\sqrt{2\pi \delta^2}} exp(-\frac{(x-\mu)^2}{2\delta^2})\) 参数$\mu$代表样本均值 ， $\delta$表示样本的标准差

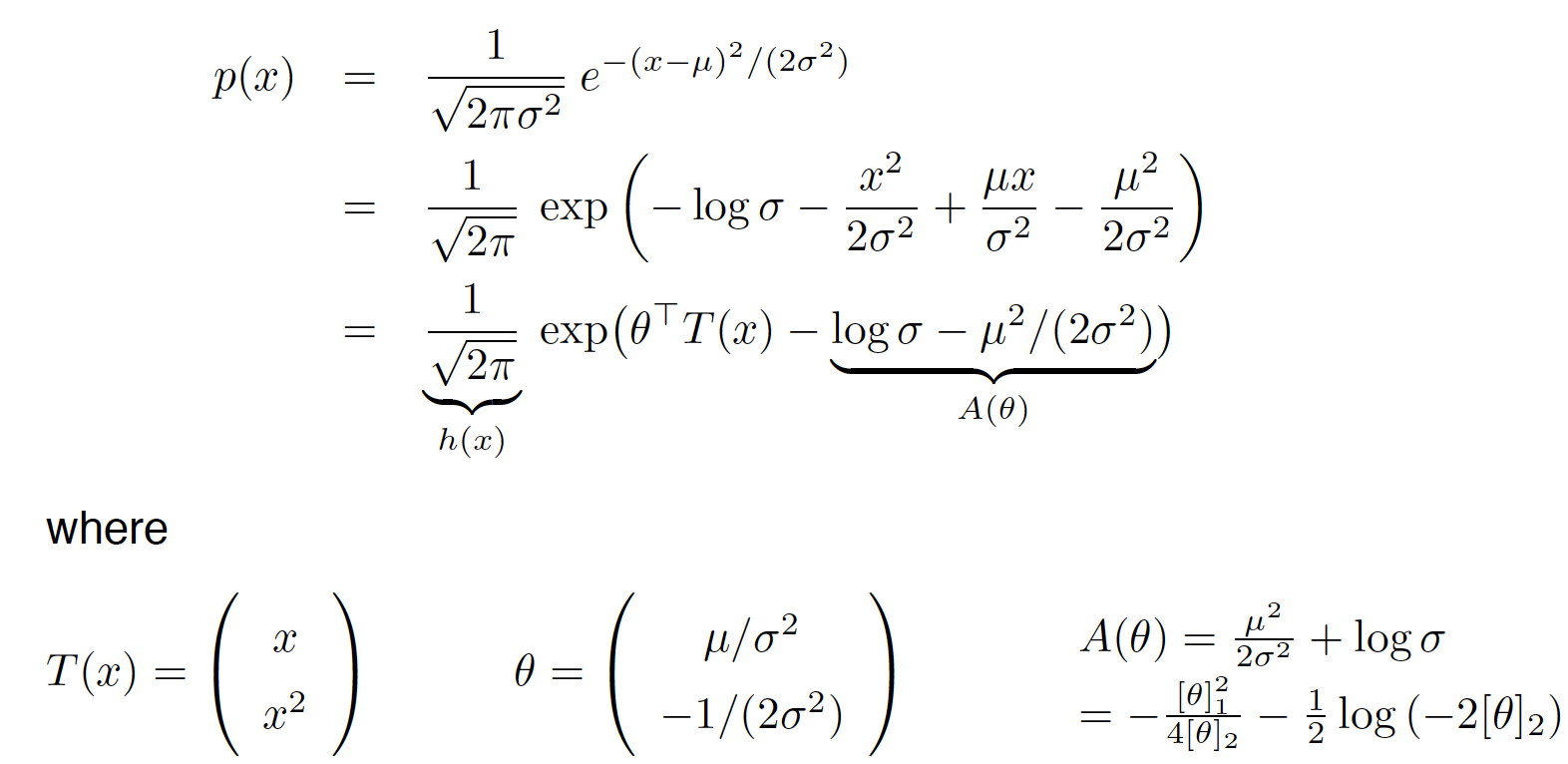
所以单变量高斯分布也属于指数分布族

多变量高斯分布

标准形式为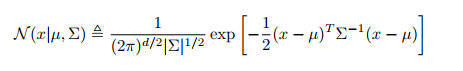： 写成指数族形式：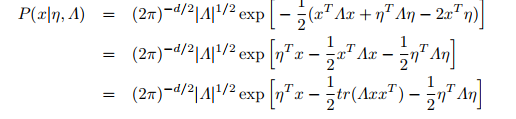

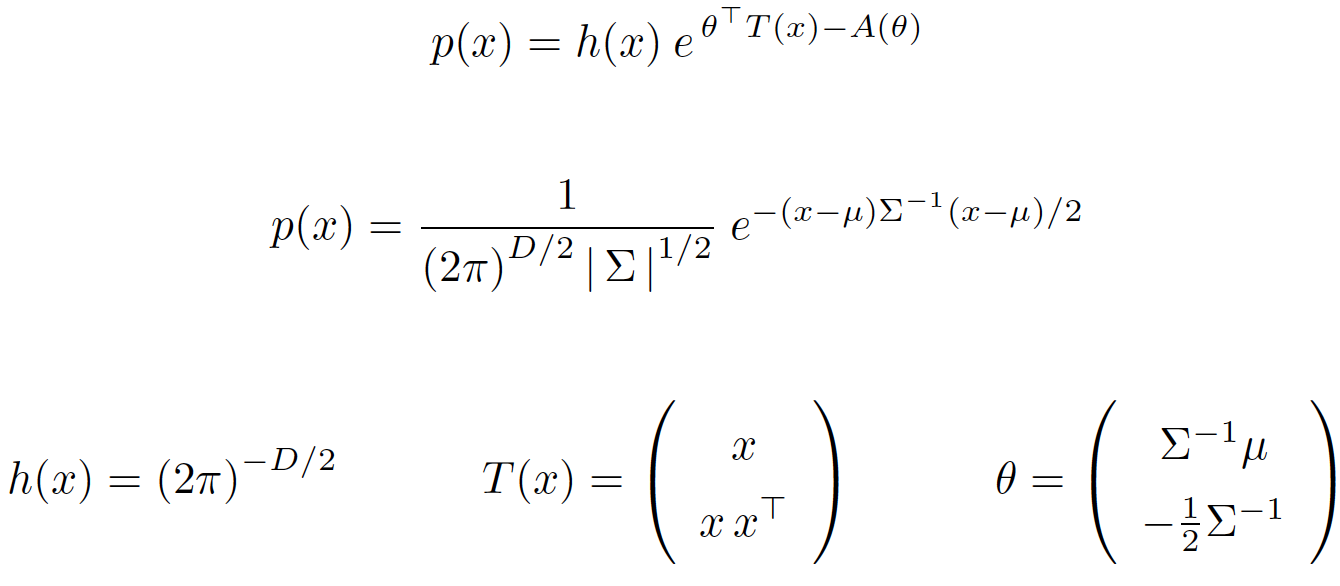
多项式分布 Multinomial

多项式分布（Multinomial Distribution）是二项式分布的推广。

二项分布的典型例子是扔硬币，硬币正面朝上概率为p, 重复扔n次硬币，k次为正面的概率即为一个二项分布概率。把二项分布公式推广至多种状态，就得到了多项分布。

某随机实验如果有$k$​​​​个可能结局$A_1、A_2、…、A_k$​​​​，分别将他们的出现次数记为随机变量$X_1、X_2、…、X_k$​​​​，它们的概率分布分别是$p_1，p_2，…，p_k$​​​​，那么在$N$​​​​次采样的总结果中，$A_1$​​​​出现$m_1$​​​​次、$A_2$​​​​​出现$m_2$​​​​次、…、$A_k$​​​​出现$m_k$​​​​次的这种事件的出现概率$P$​​​​有下面公式

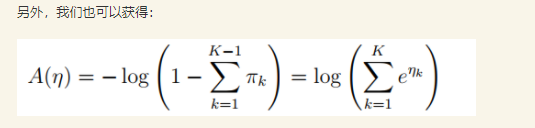
假设

为了给问题构造GLM模型，必须首先知道GLM模型的三个假设

1. $y	x;\eta \thicksim ExponentialFamily(\eta)$​​​ .

比如给定样本$x$​​​​与参数$\eta$​​​​，样本的分类$y$​​​​服从以$\eta$​​​​为参数的​指数分布族中的某个分布

1. 给定$x$，广义线性模型的目标是求解$T(y)

   x$ 来预测$T(y)$的期望， 即给定样本$x$的分类 。

不过由于很多情况下$T(y)=y$​​，所以我们的目标就变成了$h(x)=E[y

x;\theta]$​。即给定样本$x$估计的目标就是输出$E[T(y)

x]=E[y

x]$。​​

1. $\eta=\theta^T x$​ .

即自然参数$\eta(\theta)$和输入$x$满足线性关系，第3条“假设”更应该被视为一种“设计策略”，来简化模型。

三条假设，第一条是为了能在指数分布范围内讨论y的概率，第二条假设是为了使得预测值服从均值为实际值得一个分布，第三条假设是为了设计的决策函数（模型）是线性的。

最终的模型是依赖于模型服从什么样的分布，比如 高斯分布，伯努利分布。

高斯分布与最小二乘

1. 在线性回归中，我们对概率分布做出的假设是服从正态分布 $y

   x;\theta \thicksim N(\mu,\delta^2) $​

2. 我们可以将$\delta$设为1 ，那么则服从$y

   x;\theta \thicksim N(\mu,1) $​

由上面推导，我们可以得知 \(p(y;\mu) = \frac{1}{\sqrt{(2 \pi)}} exp(-\frac{1}{2}(y-\mu)^2) \\ =\frac{1}{\sqrt{(2 \pi)}} exp(-\frac{1}{2}y^2)exp(\mu y-\frac{1}{2}\mu^2 )\)

1. 根据第三个假设 $\eta=\theta^T x$

于是我们就有

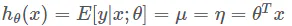
线性回归下最大似然估计与最小二乘的统一

我们发现对高斯分布做最大似然估计

伯努利分布 与逻辑回归

1. 对于二分类问题，假设$y$​​服从伯努利分布，满足第一个假设，即$y

   x;\theta \thicksim Bernoulli(\phi)$

2. 对于伯努利分布，我们得知 $P(y; \phi) = \phi^y(1-\phi)^{(1-y)} =e^{ylog\frac{\phi}{1-\phi}+log(1-\phi)}$​​

• $\eta (\theta)=log\frac{\phi}{1-\phi}$​作为自然参数 ,进而得到$\phi = \frac{1}{1+e^{-\eta}}$

• $T(y)=y$​
• $A(\theta)=log(1-\phi)=log(1+e^{\eta (\theta)})$​​
• $h(y)=1$​

1. 根据第三个假设 $\eta=\theta^T x$

我们就有 \(\phi = \frac{1}{1+e^{-\eta}} = \frac{1}{1+e^{-\theta^T x}}\\ 即 p(y=1|x;\theta) = \frac{1}{1+e^{-\theta^T x}}\)

这里的$\phi$就是伯努利分布中的概率$p$，即事件发生的概率$p(y=1)$​

在上述推导中，将概率分布的均值ϕ表示为自然参数η的函数，这样的函数称为正则响应函数，例如本例中的$\phi=g(\eta) =E[y;\eta]= \frac{1}{1+e^{-\eta}}$​。

正则响应函数的反函数$g^{-1}$​被称作正则关联函数。

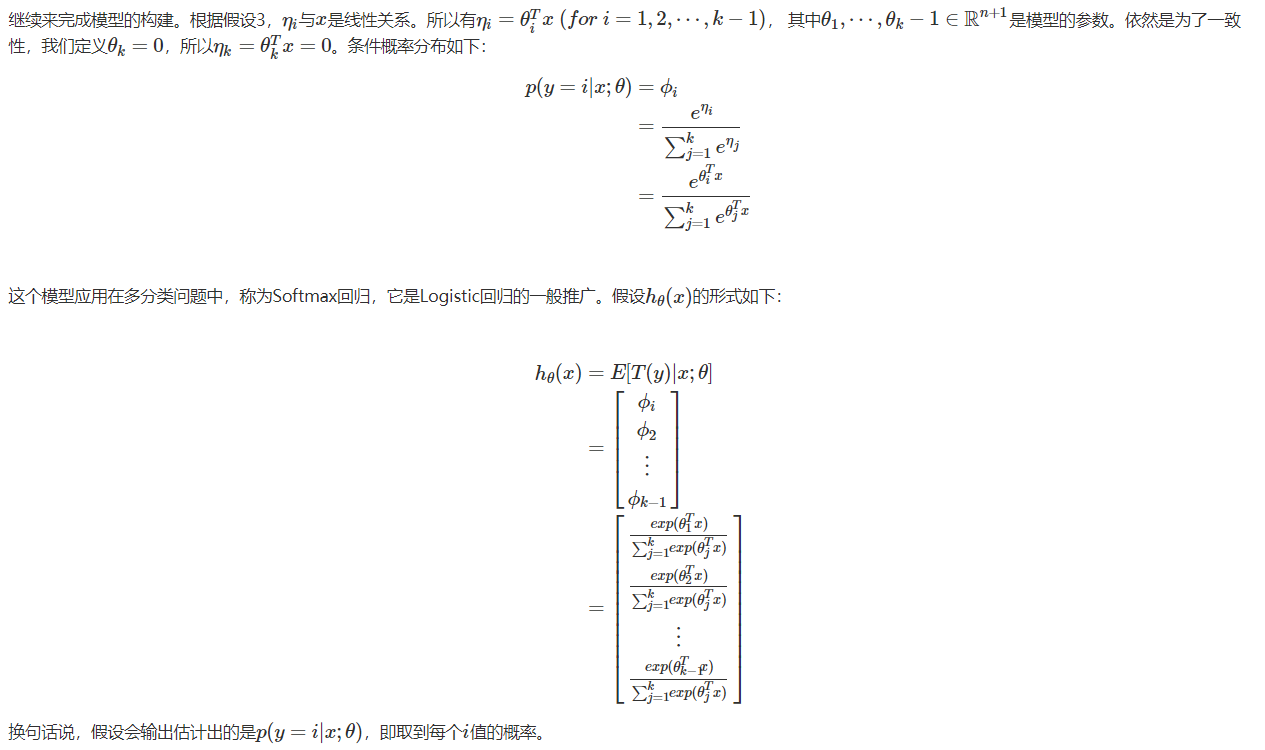
Softmax回归

再来看一个广义线性模型的例子。假设在一个多分类问题中，目标变量y有k个可能的取值，即y∈1,2,3,…,k目标变量y依然是离散值，但是可以取多个值而不是两个值。我们会用多项式模型来建立广益线行模型。

首先介绍一个可能取到k个值的多项式分布：它需要k个参数$\phi_1,\cdots,\phi_k$来表征取到每个值的概率。然而，这样表述是多余的，因为这些频率之间有一个限制条件：$\phi_1+\phi_2+\cdots + \phi_k =1$。所以我们只用$\phi_1,\cdots,\phi_{k-1}$就可以了，有时为了简便起见，我们会用$\phi_k$来代替$1-\sum_{i=1}^{k-1}\phi_i$，但要始终记得，$\phi_k$并不是一个参数。

之前的例子中，我们都是假设T(y)=y，这里我们不这样用，定义T(y)如下：

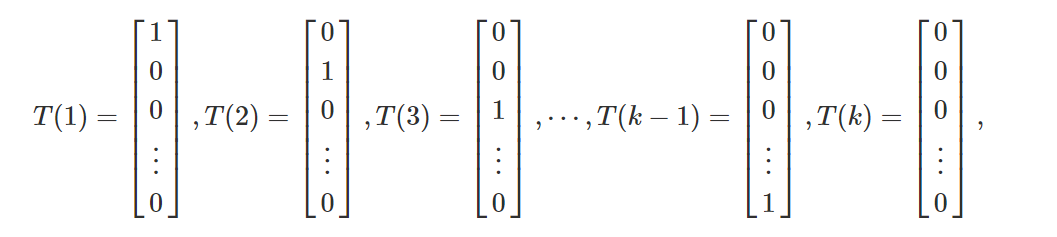
T(y)是一个k-1维的向量。我们用维的向量。我们用$(T(y))_i$来表示这个向量的第来表示这个向量的第$i-1$​个元素。

介绍另一个表达式： \1{⋅}，表示如果里面的参数是true，那么该表达式值为1；否则值为0，即$(1{true}=1,1{false}=0)$。

例如1{2=3}=0,1{3=5−2}=1。所以有以下两个结论：

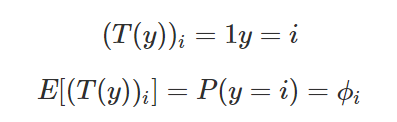
证明多项式分布属于指数分布族：

从线性回归，logistic回归，softmax回归，最大熵的概率解释来看，我们会发现线性回归是基于高斯分布+对数最大似然估计的结果，logistic回归是伯努利分布+对数最大似然估计的结果，softmax回归是多项分布+对数最大似然估计的结果，最大熵是基于期望+对数似然估计的结果。

感谢

https://www.jianshu.com/p/9c61629a1e7d

(10条消息) 指数分布族(Exponential Family)相关公式推导及在变分推断中的应用_qy20115549的博客-CSDN博客

https://fighterhit.oschina.io/2017/12/24/machine_learning_notes/%E4%BB%8E%E5%B9%BF%E4%B9%89%E7%BA%BF%E6%80%A7%E6%A8%A1%E5%9E%8B%E7%90%86%E8%A7%A3%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92/

https://blog.csdn.net/xierhacker/article/details/53364408