激活函数 Activation function
[TOC]
激活函数
1 sigmoid函数
图像
Sigmoid函数表达式
\[h(z) = \frac{1}{1+e^{-z}}\]Sigmoid求导
\[\begin{aligned} h(z)=\frac{1}{1+e^{-z}} \\ h(z)'&=(\frac{1}{1+e^{-z}} )' \\ &=\frac{e^{-z}}{(1+e^{-z})^2} \\ &=\frac{1+e^{-z}-1}{(1+e^{-z})^2} \\ &=\frac{1}{(1+e^{-z})}(1-\frac{1}{(1+e^{-z})}) \\ &=h(z)(1-h(z)) \end {aligned}\]交叉熵损失函数与Sigmoid函数求导
\[J(\theta)=- \frac{1}{m}[\sum^m_iy^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] \\ h_\theta(x^{(i)})=\frac{1}{1+e^{-\theta^Tx^{(i)}}} \\ \begin{aligned} \frac{\partial(h_\theta(x),y)}{\partial\theta_j} &= -\frac{1}{m}\sum_{i=1}^m [\frac{y^i}{h_\theta(x^{(i)})} \cdot \frac{\partial h_\theta(x^{(i)})}{\partial\theta_j}+\frac{1-y^i}{1-h_\theta(x^{(i)})} \cdot -\frac{\partial h_\theta(x^i)}{\partial\theta_j}] \\ &= -\frac{1}{m}\sum_{i=1}^m [(\frac{y}{h_\theta(x^{(i)})}-\frac{1-y}{1-h_\theta(x^{(i)})})\frac{\partial h_\theta(x^{(i)})}{\partial\theta_j}] \\ &=-\frac{1}{m}\sum_{i=1}^m [(\frac{y-h_{\theta}(x^{(i)})}{h_{\theta}(x^{(i)})(1-h_{\theta}(x^{(i)}))} )h_\theta(x^{(i)})(1-h_\theta(x^{(i)}))x_j^{(i)}] \\ &=\frac{1}{m}\sum_{i=1}^m[(h_\theta(x^{(i)})-y)x^{(i)}_j] \end{aligned}\]复合函数求导法则
对$ylog(h_\theta(x))$求导
\(\frac{\partial ylog(h_\theta(x))}{\partial \theta} = \frac{y}{h_\theta(x)} \cdot \frac{\partial h_\theta(x)}{\partial\theta}\) 对$(1-y)log(1-h_\theta(x))$求导
\(\frac{\partial (1-y)log(1-h_\theta(x))}{\partial \theta} = \frac{1-y}{1-h_\theta(x)} \cdot -\frac{\partial h_\theta(x)}{\partial\theta}\) $h_\theta’(z)=h_\theta(z)(1-h_\theta(z))$$z = \theta \cdot x$ \(\frac{\partial h_\theta(x^{(i)})}{\partial\theta_j} =h_\theta(x^{(i)})(1-h_\theta(x^{(i)})) \frac{\partial(z^{i})}{\partial{\theta_j}} \\ = h_\theta(x^{(i)})(1-h_\theta(x^{(i)})) x_j^{(i)}\)
向量形式
前面都是元素表示的形式,只是写法不同,过程基本都是一样的,不过写成向量形式会更清晰,这样就会把 $i$和求和符号 $\sum$省略掉了。我们不妨忽略前面的固定系数项$1/m$,交叉墒的损失函数(1)则可以写成下式: \(J(\theta)=-[y^Tlog \ h_\theta(x)+(1-y^T)log(1-h_\theta(x))]\) 将$h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}$带入,得到: $$ \begin{aligned} J(\theta) &=-[y^Tlog\frac{1}{1+e^{-\theta^Tx}}+(1-y^T)log\frac{1}{1+e^{-\theta^Tx}}]
&=-[-y^Tlog(1+e^{-\theta^Tx})+(1-y^T)log\ e^{-\theta^Tx}-(1-y^T)log(1+e^{-\theta^Tx})]
&=-[(1-y^T)log\ e^{-\theta^Tx}-log(1+e^{-\theta^Tx})]
&=-[(1-y^T)(-\theta^Tx)-log(1+e^{-\theta^Tx})]
\end{aligned} \(再对$\theta$求导\) \begin{aligned} \frac{\partial }{\partial\theta_j}J(\theta)
&=\frac{\partial }{\partial\theta_j}-[(1-y^T)(-\theta^Tx)-log(1+e^{-\theta^Tx})]
&=(1-y^T)x-\frac{e^{-\theta^Tx}}{1+e^{-\theta^Tx}}x
&=(\frac{1}{1+e^{-\theta^Tx}}-y^T)x
&=(h_\theta(x)-y^T)
\end{aligned} $$
转载请注明出处Jason Zhao的知乎专栏“人工+智能“,文章链接:
优缺点
在什么情况下适合使用 Sigmoid 激活函数呢?
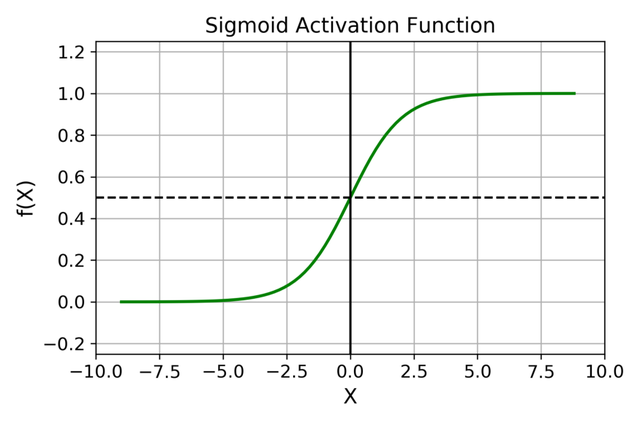
Sigmoid 函数的输出范围是 0 到 1。
由于输出值限定在 0 到 1,因此它对每个神经元的输出进行了归一化;
- 用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1,因此 Sigmoid 函数非常合适;
梯度平滑,避免「跳跃」的输出值;
函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率;
- 明确的预测,即非常接近 1 或 0。
Sigmoid 激活函数有哪些缺点?
- 倾向于梯度消失;具体来说,在反向传播的过程中,sigmoid的梯度会包含了一个 $f’(x)$ 因子(sigmoid关于输入的导数),因此一旦输入落入两端的饱和区, $f’(x)$就会变得接近于0,导致反向传播的梯度也变得非常小,此时网络参数可能甚至得不到更新,难以有效训练,这种现象称为梯度消失。一般来说,sigmoid网络在5层之内就会产生梯度消失现象。
- 函数输出不是以 0 为中心的,这会降低权重更新的效率;即激活函数的偏移现象。sigmoid函数的输出值均大于0,使得输出不是0的均值,这会导致后一层的神经元将得到上一层非0均值的信号作为输入。
- Sigmoid 函数执行指数运算,计算机运行得较慢。
2 tanh 双曲正切函数
图像
表达式
\[\begin{aligned} g(z)=\frac{1}{1+e^{-z}} \\ tanh(x&)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \\ &=2 g(2x)-1=2 \frac{1}{1+e^{-2x}}-1\ \end{aligned}\]求导
\[\begin{aligned} tanh'(x)&=[\frac{e^x-e^{-x}}{e^x+e^{-x}}]'\\ &= \frac{(e^x+e^{-x})(e^x+e^{-x})-(e^x-e^{-x})(e^x-e^{-x})}{(e^x+e^{-x})^2}\\ &=1-\frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \\ &=1-tanh^2(x) \\ tanh'(x)&= [2\frac{1}{1+e^{-2x}}-1 ]' \\ &=\frac{4e^{-2x}}{(e^{-2x}+1)^2} \\ &=2tanh(x)[1-tanh(x)] \end{aligned}\]优缺点
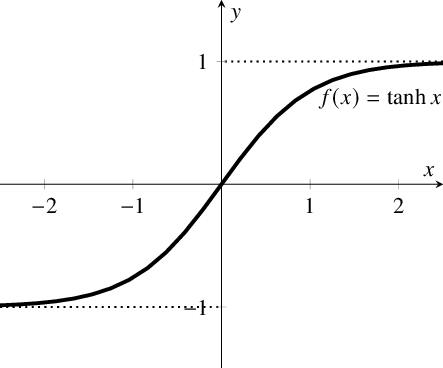
tanh 是一个双曲正切函数。tanh 函数和 sigmoid 函数的曲线相对相似。但是它比 sigmoid 函数更有一些优势。
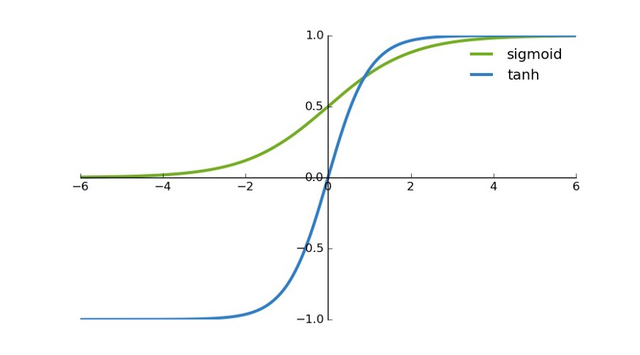
首先,当输入较大或较小时,输出几乎是平滑的并且梯度较小,这不利于权重更新。
二者的区别在于输出间隔,tanh 的输出间隔为 1,并且整个函数以 0 为中心,比 sigmoid 函数更好;在 tanh 图中,负输入将被强映射为负,而零输入被映射为接近零。
注意:在一般的二元分类问题中,tanh 函数用于隐藏层,而 sigmoid 函数用于输出层,但这并不是固定的,需要根据特定问题进行调整。
3 ReLu
图像
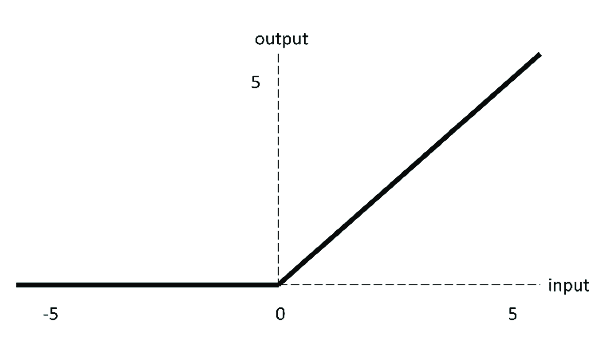
表达式
\[\begin{equation} ReLu(x)= max(0,x)= \begin{cases} x &x> 0\\ 0 & x\leq0 \\ \end{cases} \end{equation}\]求导
\[\begin{equation} ReLu'(x)= max(0,x)'= \begin{cases} 1 & Relu(x)> ,x>0\\ 0 & Relu(x) =0 ,x\leq0\\ \end{cases} \end{equation}\]优缺点
ReLU 函数是深度学习中较为流行的一种激活函数,相比于 sigmoid 函数和 tanh 函数,它具有如下优点:
- 当输入为正时,不存在梯度饱和问题。计算速度快得多。
- ReLU 函数中只存在线性关系,因此它的计算速度比 sigmoid 和 tanh 更快。
当然,它也有缺点:
- Dead ReLU 问题。当输入为负时,ReLU 完全失效,在正向传播过程中,这不是问题。有些区域很敏感,有些则不敏感。但是在反向传播过程中,如果输入负数,则梯度将完全为零,sigmoid 函数和 tanh 函数也具有相同的问题;
- 我们发现 ReLU 函数的输出为 0 或正数,这意味着 ReLU 函数不是以 0 为中心的函数。
4 Softmax
图像
表达式
\[S_i=Softmax(z_i)=\frac{e^{z_i}}{\sum^K_{l=1}e^{z_l}}\]softmax函数,又称归一化指数函数。它是二分类函数sigmoid在多分类上的推广。
softmax就是模型已经有分类预测结果以后,将预测结果输入softmax函数,进行非负性和归一化处理,最后得到0-1之内的分类概率。
总结一下softmax如何将多分类输出转换为概率,可以分为两步:
1)分子:通过指数函数,将实数输出映射到零到正无穷。
2)分母:将所有结果相加,进行归一化。
求导
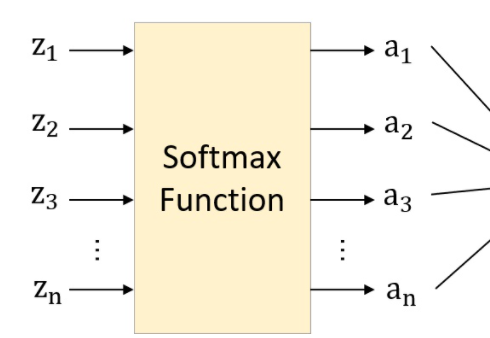
输入是一个向量$z=[z_1,z_2,\cdots,z_n]$,维度为(1,n)
输出也是一个向量$a=[a_1,a_2,\cdots,a_n],a_i=\frac{e^{z_i}}{\sum_{k=1}^ne^{z_k}}$,
所以softamx函数是一个$R^N \rightarrow R^N$的函数,它的导数是一个雅克比矩阵
在计算之前我们首先要明确:
- 我们想要计算softmax的哪个组成成分(输出的某元素)的导数。
- 由于softmax具有多个输入,所以要计算关于哪个输入元素的偏导
即偏导$\frac{\partial S_i}{\partial z_j}=\frac{\partial a_i}{\partial z_j}$,这是第$i$个输出关于第$j$个输入的偏导
这样我们最终计算出的雅克比矩阵形式为 \(\begin{equation*} \frac{\partial a}{\partial z}= \begin{bmatrix} \frac{\partial a_1}{\partial z_1} & \cdots\ &\frac{\partial a_1}{\partial z_n}\\ \vdots & \ddots & \vdots \\ \frac{\partial a_n}{\partial z_1} & \cdots\ & \frac{\partial a_n}{\partial z_n}\ \end{bmatrix} \end{equation*}\) 对任意的$i,j$,我们计算$D_jS_i$: \(\begin{equation*} \frac{\partial S_i}{\partial z_j} =\frac{\partial a_i}{\partial z_j} =\frac{\partial \frac{e^{z_i}}{\sum_{k=1}^{N}e^{z_k}}}{\partial z_j} \end{equation*}\) 我们使用链式法则进行求解
对于分式形式的函数$f(x)=\frac{g(x)}{h(x)}$: \(f'(x)=\frac{g'(x)h(x)-g(x)h'(x)}{[h(x)]^2}\) 在我们的情形下有: \(g_i=e^{z_i} \\ h_i = \sum_{k=1}^N e^{z_k}\) 注意:对于$h_i$,无论是求哪个$z_j$的导数,结果都是$e^{z_j}$
但是对于$g_i$,其关于$z_j$的倒数是$e^{z_j}$当且仅当$i=j$;否则结果为0
我们先考虑$i=j$的情况: \(\begin{equation*} \begin{split} \frac{\partial \frac{e^{z_i}}{\sum_{k=1}^{N}e^{z_k}}}{\partial z_j}= \frac{e^{z_i}\sum_k^ne^{z_k}-e^{z_j}e^{z_i}}{(\sum_k^ne^{z_k})^2 } \\ =\frac{e^{z_i}}{\sum_k^ne^{z_k} } \times \frac{\sum_k^ne^{z_k}-e^{z_j}}{\sum_k^ne^{z_k}} \\ =s_i(1-s_j) \\ =a_i(1-a_j) \end{split} \end{equation*}\) 最后的公式使用其自身来表示 $s_i,s_j$,这在包含指数函数时是一个常用的技巧。
考虑$i \neq j$的情况: \(\begin{equation*} \begin{split} \frac{\partial \frac{e^{z_i}}{\sum_{k=1}^{N}e^{z_k}}}{\partial z_j}= \frac{0-e^{z_j}e^{z_i}}{(\sum_k^ne^{z_k})^2 } \\ =-\frac{e^{z_j}}{\sum_k^ne^{z_k} } \times \frac{e^{z_i}}{\sum_k^ne^{z_k}} \\ =-s_js_i \\ =-a_ja_i \end{split} \end{equation*}\) 总结 \(\begin{equation*} \frac{\partial a_i}{\partial z_j}=\left\{\begin{matrix} a_i(1-a_j) & i=j\\ -a_ja_i & i\neq j \end{matrix}\right. \end{equation*}\) 在文献中我们常常会见到各种各样的”浓缩的”公式,一个常见的例子是使用克罗内克函数: \(\begin{equation*} \delta_{ij}=\left \{\begin{matrix} 1 & i=j\\ 0 & i\neq j \end{matrix}\right. \end{equation*}\) 于是有 \(\begin{equation*} \frac{\partial a_i}{\partial z_j}=a_i(\delta_{ij}-a_j) \end{equation*}\) 在文献中也有一些其它的表述:
- 在雅可比矩阵中使用单位矩阵$I$来替换$\delta$,$I$使用元素的矩阵形式表示了$\delta$。
- 使用示性函数”$1$”作为函数名而不是克罗内克$\delta$,如下所示:$\frac{\partial a_i}{\partial z_j}=a_i(1(i=j)-a_j)$。这里$1(j=j)$意味着当$i=j$时值为1,否则为$0$。
当我们想要计算依赖于softmax导数的更复杂的导数时,“浓缩”符号会很有用; 否则我们必须在任何地方完整的写出公式。
Softmax层求导
交叉熵损失函数与Softmax函数求导
Softmax 是用于多类分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量,Softmax 可以将其压缩为长度为 K,值在(0,1)范围内,并且向量中元素的总和为 1 的实向量。
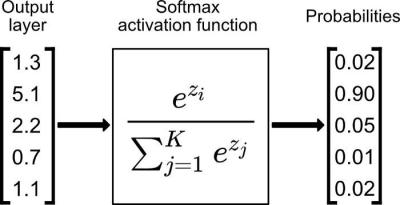
Softmax激活后,结果是一个在各个分类上的概率,在K个分类中,经过变换后的样本$z=\theta^Tx^{(i)}$属于类别$j$的概率 \(softmax(z=\theta^T_jx^{(i)})=P(y^{(i)} =j| x^{(i)};\theta) =\frac{exp\{\theta^T_jx^{(i)}\}}{\sum_{l=1}^k exp\{\theta^T_l x^{(i)}\}}\) 我们使用交叉熵作为损失函数
我们定义唯一的$y^{(i)}=1$的索引为$j$,因此对所有的$j\neq y^{(i)}$,都有$y^j=0$,于是交叉熵损失可以简化 \(\begin{aligned} J(\theta) &=-\frac{1}{m}[\sum_{i=1}^m\sum_{j=1}^k 1 \cdot log\ P(y^{(i)}=j| x^{(i)};\theta) \}] \\ &=-\frac{1}{m}[\sum_{i=1}^m\sum_{j=1}^k 1 \{ y^{(i)}=j\}\cdot log\frac{exp\{\theta^T_jx^{(i)}\}}{\sum_{l=1}^k exp\{\theta^T_l x^{(i)}\}}] \\ &=-\frac{1}{m}\sum_{i=1}^m\sum_{j=1}^k 1 \{ y^{(i)}=j\} \cdot[\theta^T_jx^{(i)}-log \sum_{l=1}^k exp\{\theta^T_l x^{(i)}\}] \end{aligned}\) 在损失函数上添加L2正则化项 \(J(\theta)=-\frac{1}{m}[\sum_{i=1}^m\sum_{j=1}^k 1 \{ y^{(i)}=j\}\cdot log\frac{exp\{\theta^T_jx^{(i)}\}}{\sum_{l=1}^k exp\{\theta^T_l x^{(i)}\}}]+\frac{\lambda}{2}\sum_{i=1}^k\sum_{j=0}^n\theta_{ij}^2\) 直接推导 $$ \begin{aligned} \bigtriangledown_{\theta_i}J(\theta) &= -\frac{1}{m}\sum_{i=1}^m\sum_{j=1}^k 1 { y^{(i)}=j} \cdot [x^{(i)}-\frac{x^{(i)}exp{\theta^Tx^{(i)}}}{\sum_{l=1}^k exp{\theta^T_l x^{(i)}}}]
&= -\frac{1}{m}\sum_{i=1}^m\sum_{j=1}^k 1 { y^{(i)}=j} \cdot x^{(i)}[1-\frac{exp{\theta^Tx^{(i)}}}{\sum_{l=1}^k exp{\theta^T_l x^{(i)}}}]
&=-\frac{1}{m}\sum_{i=1}^m[x^{(i)}1 {y^{(i)}=j}\cdot (1-P(y^{(i)}=j| x^{(i)};\theta))]
\end{aligned} $$
交叉熵损失函数:
交叉熵函数$H(p,q)=-\sum_{i=1}^np(x_i)\cdot log\ q(x_i)$
输入元素的Label就是真实的分布$p(x)$,我们得到的分布$a=[a_1,\cdots,a_n]$是拟合得到的分布,我们要用交叉熵函数来刻画两个分布之间的差异,也就是我们拟合的效果
则交叉熵损失函数为$H(y,a)=-\sum_{i=1}^ny_i \cdot ln(a_i)$,$n$表示标签的类别有$n$个
Label是输入数据的真实标签,为已知量,一般为one-hot编码格式,其中一个元素为1,表示正确的类别,其他为0。我们不妨假设第j个类别是正确的,则$y=[0,0,\cdots,1,\cdots,0]$,只有$y_j=1$,其余$y_i=0$
则交叉熵损失函数简化为$L=H(y,a)=-y_j\cdot ln(a_j)=-ln(a_j)$
损失函数$L$是标量,维度为$(1,1)$
我们来求标量$L$对向量$z$的导数$\frac{\partial L}{\partial z}$,根据链式法则$\frac{\partial L}{\partial z}=\frac{\partial L}{\partial a}*\frac{\partial a}{\partial z}$,其中$a,z$为维度为$(1,n)$的向量
标量对向量求导,维度不变 \(f(x)=f(x_1,x_2,\cdots,x_n)\\ \frac{\partial f}{\partial x}=[\frac{\partial f}{\partial x_1},\cdots,\frac{\partial f}{\partial x_n}]\) 所以$\frac{\partial L}{\partial z}$和$\frac{\partial L}{\partial a}$的维度都为$(1,n)$
对于$\frac{\partial a}{\partial z}$的结果是雅克比矩阵,也就是我们上面得到的结果,$\frac{\partial z}{\partial z}$的维度是$(n,n)$,所以按着矩阵计算维度是没问题的
求$\frac{\partial L}{\partial a}$
$L=-ln(a_j)$,可以知道最终损失函数只与$a_j$有关 \(\frac{\partial L}{\partial a}=[0,0,0,\cdots,-\frac{1}{a_j},\cdots,0]\)
求$\frac{\partial a}{\partial z}$
我们上面已经得知$\frac{\partial a}{\partial z}$的雅克比矩阵 \(\begin{equation*} \frac{\partial a}{\partial z}= \begin{bmatrix} \frac{\partial a_1}{\partial z_1} & \cdots\ &\frac{\partial a_1}{\partial z_n}\\ \vdots & \ddots & \vdots \\ \frac{\partial a_n}{\partial z_1} & \cdots\ & \frac{\partial a_n}{\partial z_n}\ \end{bmatrix} \end{equation*}\) 可以发现Jacobian矩阵的每一行对应着$\frac{\partial a_i}{\partial z}
由于$\frac{\partial L}{\partial a}$只有第$j$列$a_j$不为0,我们只需要求$\frac{\partial a}{\partial z}$的第$j$行,也就是$\frac{\partial a_j}{\partial z}$ \(\frac{\partial L}{\partial z}= - \frac{1}{a_j} * \frac{\partial a_j}{\partial z},\text{其中}a_j= \frac{e^{z_j}}{\sum_{k=1}^{N}e^{z_k}}\)
当$i \neq j$ $$ \begin{aligned} &\frac{\partial a_j}{\partial z_i}= -a_ja_i
&\frac{\partial L}{\partial z_i}=\frac{\partial L}{\partial a_j} \cdot\frac{\partial a_j}{\partial z_i}=-\frac{1}{a_j} \cdot(-a_ja_i)=a_i\end{aligned} $$
当$i = j$ $$ \begin{aligned} &\frac{\partial a_j}{\partial z_j}= a_j-a_j^2
&\frac{\partial L}{\partial z_j}=\frac{\partial L}{\partial a_j} \cdot\frac{\partial a_j}{\partial z_j}=-\frac{1}{a_j} \cdot(a_j-a_j^2)=a_j-1\end{aligned} $$
综上 \(\frac{\partial L}{\partial z}=[a_1,a_2,\cdots,a_j-1,\cdots,a_n]=a-y \\ a=[a_1,a_2,\cdots,a_j,\cdots,a_n],y=[0,0,\cdots,1,\cdots,0]\) Softmax Cross Entropy Loss的求导结果非常优雅,就等于预测值与Label的差。
优缺点
Softmax 与正常的 max 函数不同:max 函数仅输出最大值,但 Softmax 确保较小的值具有较小的概率,并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。
Softmax 函数的分母结合了原始输出值的所有因子,这意味着 Softmax 函数获得的各种概率彼此相关。
Softmax 激活函数的主要缺点是:
在零点不可微;
负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
文档信息
- 本文作者:zuti666
- 本文链接:https://zuti666.github.io/2023/08/02/activation-function/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
