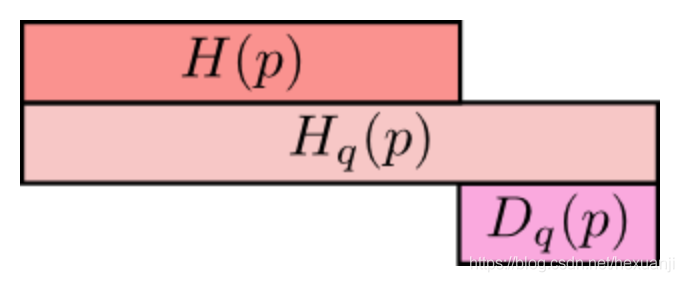Information Theory –Information content、Entropy, Relative Entropy, Cross Entropy

信息论——信息量、熵、相对熵、交叉熵、JS Divergence ,Wasserstein distance

阅读链接

https://www.cnblogs.com/kyrieng/p/8694705.html

问题

比较模型，同一下模型，可以比较

如何衡量和比较不同模型

熵

描述混乱程度

热力学，信息论

信息量 Information content

如何定义信息量

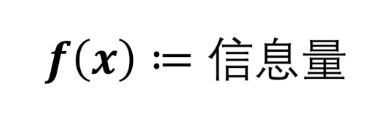
• 自洽，

• 符合现实的直觉

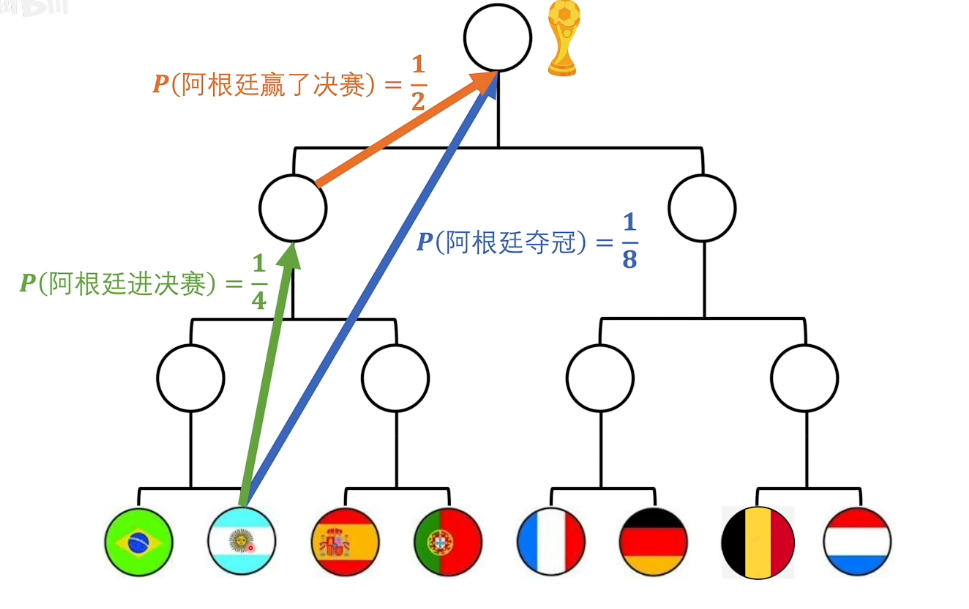
1. 直观上的直觉：阿根廷夺冠包含的信息量应该包含阿根廷进决赛和阿根廷赢了决赛这两个事件。
2. 体系上的自洽：从概率论出发，我们可以得到上面两个事件的概率，它们满足概率相乘的公式

因此就会有如下两条要求

概率论中的相乘运算要满足我们这里定义的两个事件的信息量相加的直觉。

相乘变成相加，一个直接的操作就是取 log

所以我们就能够得到

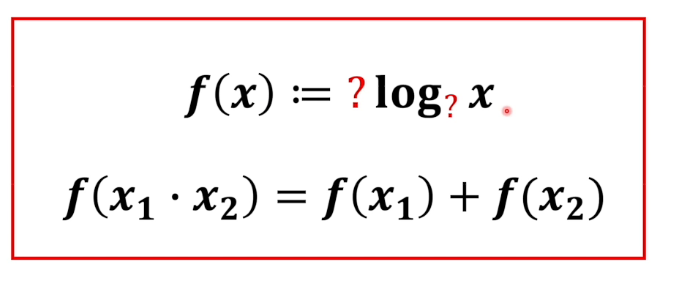
接下来我们要确定这一个系数和log函数的底

首先这个系数来怎么确定

一个很简单的想法是1，但在这里可能是不合适的，

因为我们从上面得知，阿根廷夺冠的概率是$1/8$, 这个事件包含的信息量应该比 阿根廷进决赛（概率$1/4$）和阿根廷赢了决赛(概率$1/2$) 都要大。而$log$函数是一个递增函数，所以我们需要将其转换方向，加一个符号。这样结果就是 事件对应概率越大，它的信息量越小。这和上面的举例以及我们的直观感觉是一致的。

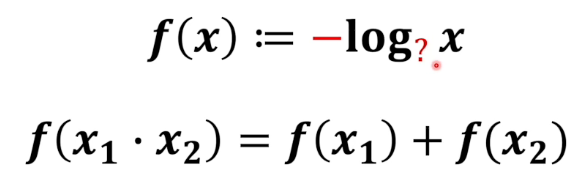
其次是，log函数的底是什么。这个已经无关紧要了，因为它可以取$e$也可以取$2$等，它不影响我们定义这个概念要处理的自洽问题。我们不妨就取$2$。

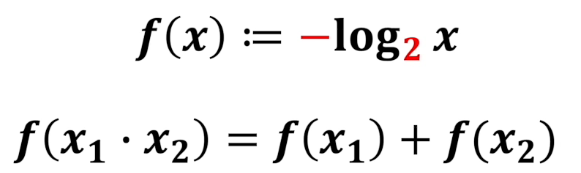
其实以2为底，计算出来的信息量是由单位的，这个单位就是比特

可以认为衡量信息量大小的单位就是抛硬币

例如，给计算机输入一个16位的数据，在你输入这个数据之前这16位出现的任一数字的可能性为$\frac{1}{2^{16}}$，而当你输入之后，这个数据就一下确定下来了，只有一个可能性被确定，可能性变成了1。所以这16位数字的信息量就是16比特。

信息量就可以理解为一个事件从不确定变成确定，它的难度有多大。信息量比较大就说明这个难度比较高。

信息论的基本想法是，一个不太可能的事件发生了的话，要比一个非常可能发生的事件提供更多的信息。如果想通过这种想法来量化信息，需要满足以下性质：

1. 非常可能发生的事件信息量比较少，并且极端情况下，确定能够发生的事件没有信息量。
2. 较不可能发生的事件具有更高的信息量。
3. 独立事件应具有增量的信息。例如，投掷的硬币两次正面朝上传递的信息量，应该是投掷一次硬币正面朝上的信息量的两倍。

熵 Entropy

熵的概念类似，只不过熵不是衡量某一个具体事件，而是衡量整个系统的不确定性。也就是整个系统从不确定变成确定的难度。

下面如何确定熵的定义呢，下面给一个例子。下面是两场比赛，两个系统，我们可以根据上面信息量的定义计算出系统中事件的信息量如下。

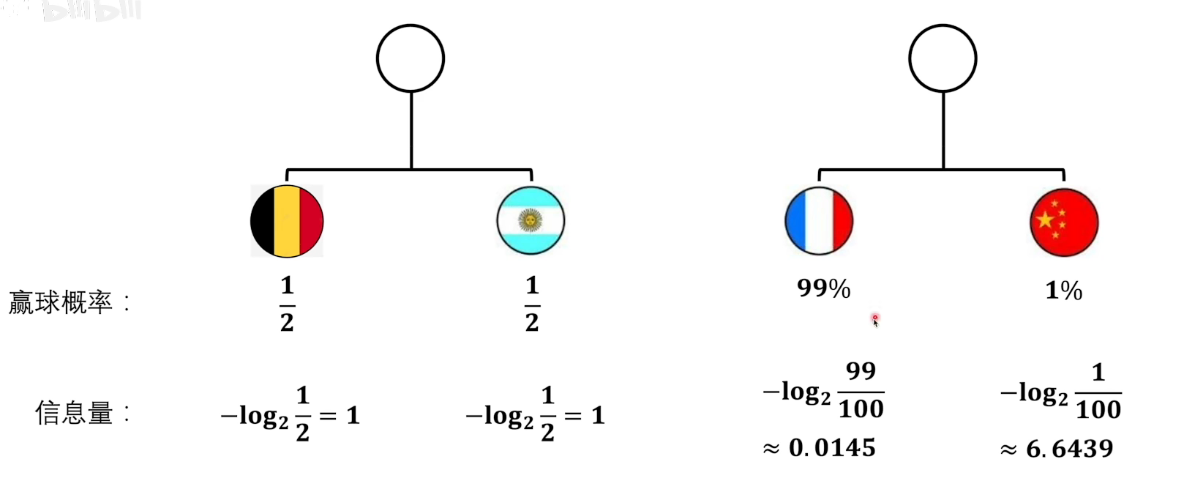
那么整个系统的熵是怎么计算呢？是直接加起来吗。

我们看，第二场比赛，法国赢球的概率是99%，那么第二场比赛的结果的确定性就越高。第一场比赛，两方赢球的概率都是$1/2$，显然这个比赛的结果的不确定性更大，所以对应我们的直觉，这个系统的熵应该更大。但如果是直接加起来，显然后面的数值更大，这与我们上面的想法是不一致的。因为熵越大代表着整个系统的不确定性越大，混乱程度越大。

另外，我们看，中国赢球的信息量很大，但是概率很低。而只有当中国赢球这个事件发生了之后，我们才能获得这个信息量6.5。所以对于整个比赛，单个事件的贡献，应该再乘以这个事件发生的概率。

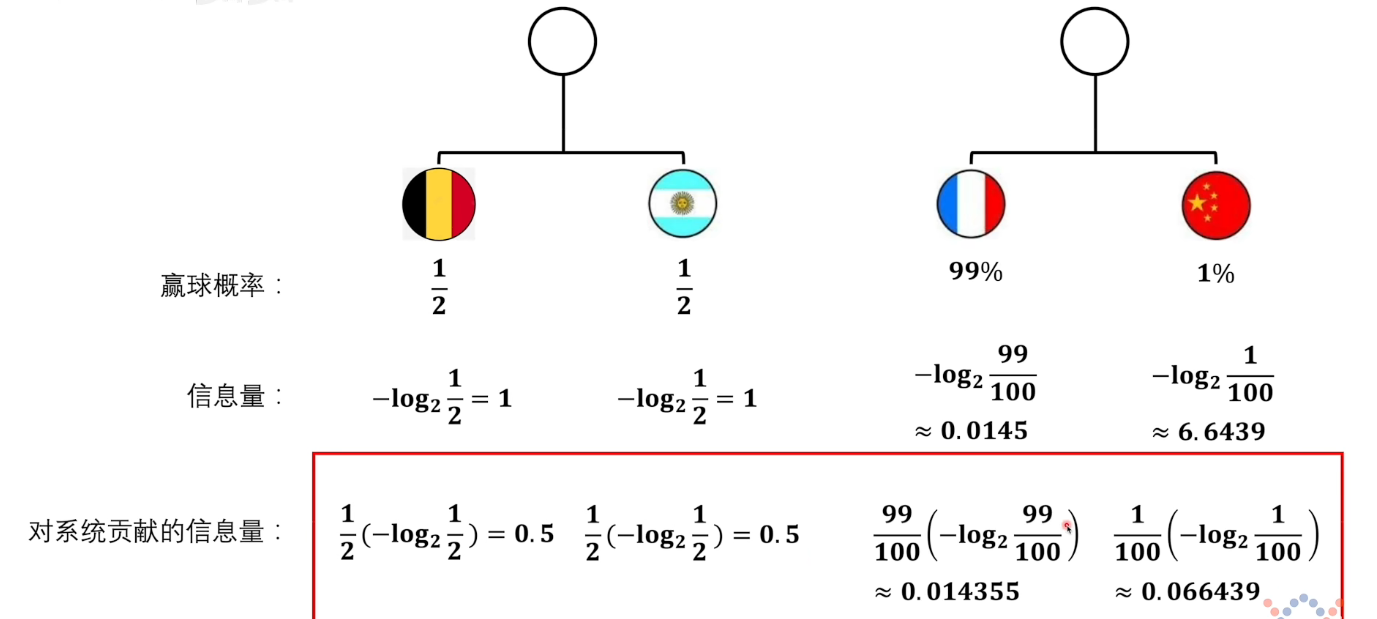
看到下面这个式子，其实就是期望的定义。

因此，我们就有了系统的熵的定义

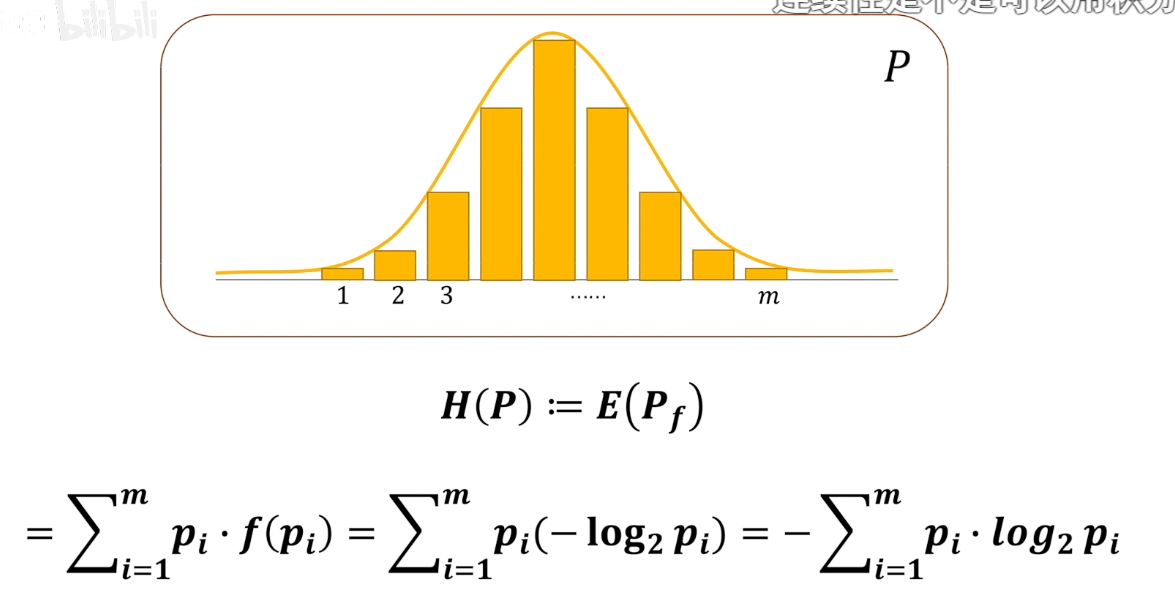
信息熵具有以下性质：

• 单调性，即发生概率越高的事件，其所携带的信息熵越低。极端案例就是“太阳从东方升起”，因为为确定事件，所以不携带任何信息量。从信息论的角度，认为这句话没有消除任何不确定性。
• 非负性，即信息熵不能为负。这个很好理解，因为负的信息，即你得知了某个信息后，却增加了不确定性是不合逻辑的。
• 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和。

0-1分布问题（二项分布的特例），熵的计算方法可以简化为如下算式： \(H(X) = - \sum_{i=1}^n p(x_i)log p(x_i) = -p(x)log(p(x)) - (1-p(x))log(1-p(x))\)

相对熵 KL散度 Relative Entropy

相对熵，肯定是关于两个系统。

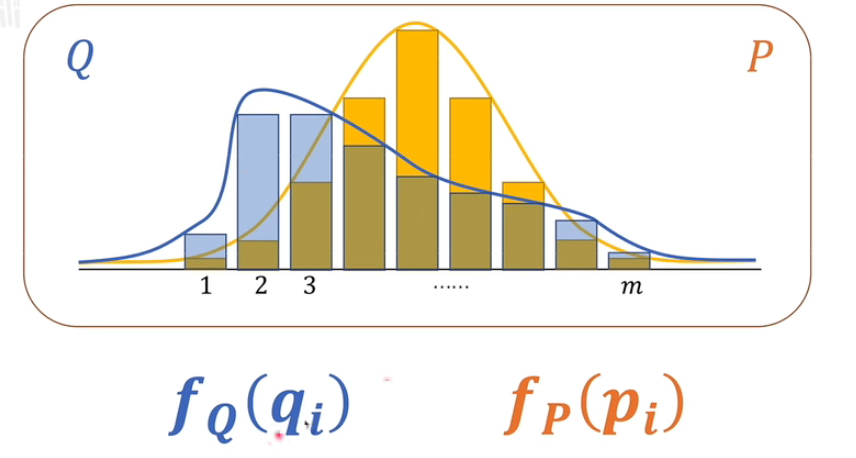
上面是两个系统 P.Q。图为概率分布图，下面是系统的信息量。

下面我们看KL散度的定义 \(\begin{aligned} & \boldsymbol{D}_{\boldsymbol{K} \boldsymbol{L}}(\boldsymbol{P} \| \boldsymbol{Q}) \\ & :=\sum_{i=\mathbf{1}}^m p_i \cdot\left(f_Q\left(q_i\right)-f_P\left(p_i\right)\right) \\ & =\sum_{i=1}^m p_i \cdot\left(\left(-\log _2 q_i\right)-\left(-\log _2 p_i\right)\right) \\ & =\sum_{i=1}^n p(x_i) \cdot log\frac{p(x_i)}{q(x_i)} \end{aligned}\) P 在前，就表示以P为基准，去考虑P和Q相差有多少

看定义，系统Q中事件对应的信息量减去系统P中事件的信息量，然后对差求整体的期望。

当P和Q是完全相等的时候，最后结果一定是0。所以0就代表P和Q完全相等。自然KL散度不为0，那么就说明P和Q之间有差距。

直观的理解就是，P和Q不同，P要想变得和Q一样，需要补充的信息量，如果能补齐了，就能把P变成和Q一样。相对熵表示拟合真实分布时产生的信息损耗

参与计算的一个概率分布为真实分布$P$，另一个为拟合分布或者说模型预测出来的分布$Q$，相对熵表示拟合真实分布时产生的信息损耗。在机器学习中，一般p表示真实分布，而q表示预测分布

交叉熵 Cross Entropy

我们将KL散度公式进行变形 ： $$ \begin{aligned} KL(p||q) &= \sum_{i=1}^n p(x_i) \cdot log(\frac{p(x_i)}{q(x_i)})
&= \sum_{i=1}^n p(x_i) \cdot log\ p(x_i) - \sum_{i=1}^n p(x_i) \cdot log\ q(x_i)
&= -H(p(x)) + [ \sum_{i=1}^n p(x_i) \cdot - log\ q(x_i)]

\end{aligned} \(等式的前一部分恰巧就是真实分布$P$的信息熵，为恒定值。等式的后一部分，就是交叉熵\) H(p,q) =- \sum_{i=1}^n p(x_i) \cdot log\ q(x_i) $$ $n$表示分布定义的随机变量的所有可能的取值

最后我们变形得到的结果，后面

所以看P和Q是否相同，即KL散度是否为0那就要看后面的这一项

这两个值都是一个正数，那他俩关系是怎样的呢？自然就有两种情况，结果就有可能有正负。

当其实已经有了证明

交叉熵一定大于后面的，所有KL散度一定大于0，并且KL散度越大，代表P和Q差别越大。

所以我们想要使得P和Q越接近越好，那么我们就可以直接来使得交叉熵越小越好，用交叉熵来代表损失函数.

最上方$H(p)$​为信息熵，表示分布$p$的平均编码长度/信息量；

中间的$Hq(p)$表示用分布q表编码分布p所含的信息量或编码长度，简称为交叉熵，其中$Hq(p)>=H(p)$

最小方的$Dq(p)$表示的是q对p的KL距离，衡量了分布q和分布p之间的差异性，其中$Dq(p)>=0$;

从上图可知，$Hq(p) = H(p) + Dq(p)$

定义

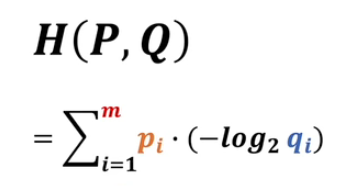
如何应用

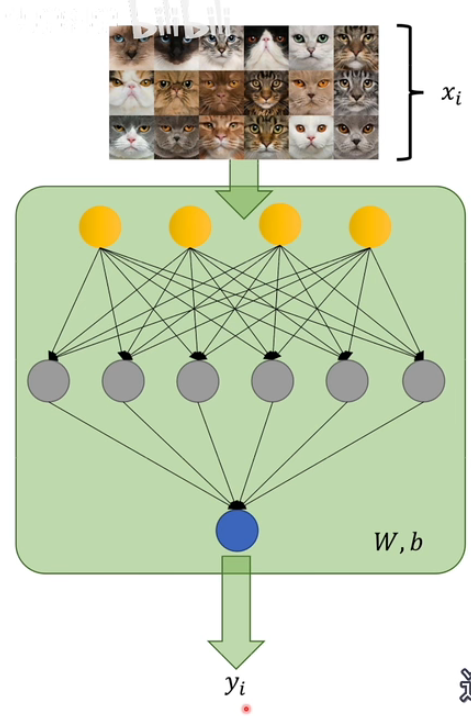
首先，这个m应该是什么，因为P和Q对应的结果可能是不一致的。很简单，把p和q里面较大的那个数字带进来就可以了。再应用的时候，就是我们输入数据x的个数n.

其次，后面这个y 是什么。我们要求两个分布P和Q对应的事件应该是一致的，那么当输入的图片是猫的时候，输出应该是猫的概率，当输入不是猫的时候，输出应该是不是猫的概率，所以还需要继续展开。

损失函数

这个损失函数和极大似然估计推导出来的结果形式上是一致的

实际上在使用最大似然估计时常取负数，通过上面的式子我们就可以看出，这样我们就发现最大似然和最小化交叉熵是等价的。（因为有一个负号，最小化交叉熵就是最大化似然，模型训练得到的效果是一样的）

但是是不同的理解思路

极大似然估计里面的log是将连乘变成连加

交叉熵里面的log和符号都是从定义来的

JS 散度

JS散度度量了两个概率分布的相似度，基于KL散度的变体，解决了KL散度非对称的问题。一般地，JS散度是对称的，其取值是0到1之间。定义如下： \(JS(P||Q) = \frac{1}{2}KL(P(x)|| \frac{P(x)+Q(x)}{2}) + \frac{1}{2}KL(Q(x)|| \frac{P(x)+Q(x)}{2})\)

• 值域范围. JS散度的值域范围是[0,1]，相同则是0，相反为1。相较于KL，对相似度的判别更确切了

• 对称性.即 $JS(P

  Q)=JS(Q

  P)$。

Wasserstein distance ( Kantorovich metric)

KL散度和JS散度度量的问题：

如果两个分布P,Q离得很远，完全没有重叠的时候，那么KL散度值是没有意义的，而JS散度值是一个常数。这在学习算法中是比较致命的，这就意味这这一点的梯度为0。梯度消失了。

Wasserstein距离度量两个概率分布之间的距离，定义如下 \(W(P_1,P_2)= inf_{\gamma \sim \Pi(P_1,P_2)} E_{(x,y)\sim \gamma}||x -y||\) 式中$\Pi(P_1,P_2)$是 $P_1$和$P_2$​ 分布组合起来的所有可能的联合分布的集合。

理解

这里描述的是两个概率分布之间的距离。这个距离不是直观的几何上的距离，距离在数学上的定义是一个宽泛的概念，只要满足非负、自反、三角不等式就可以称之为距离。

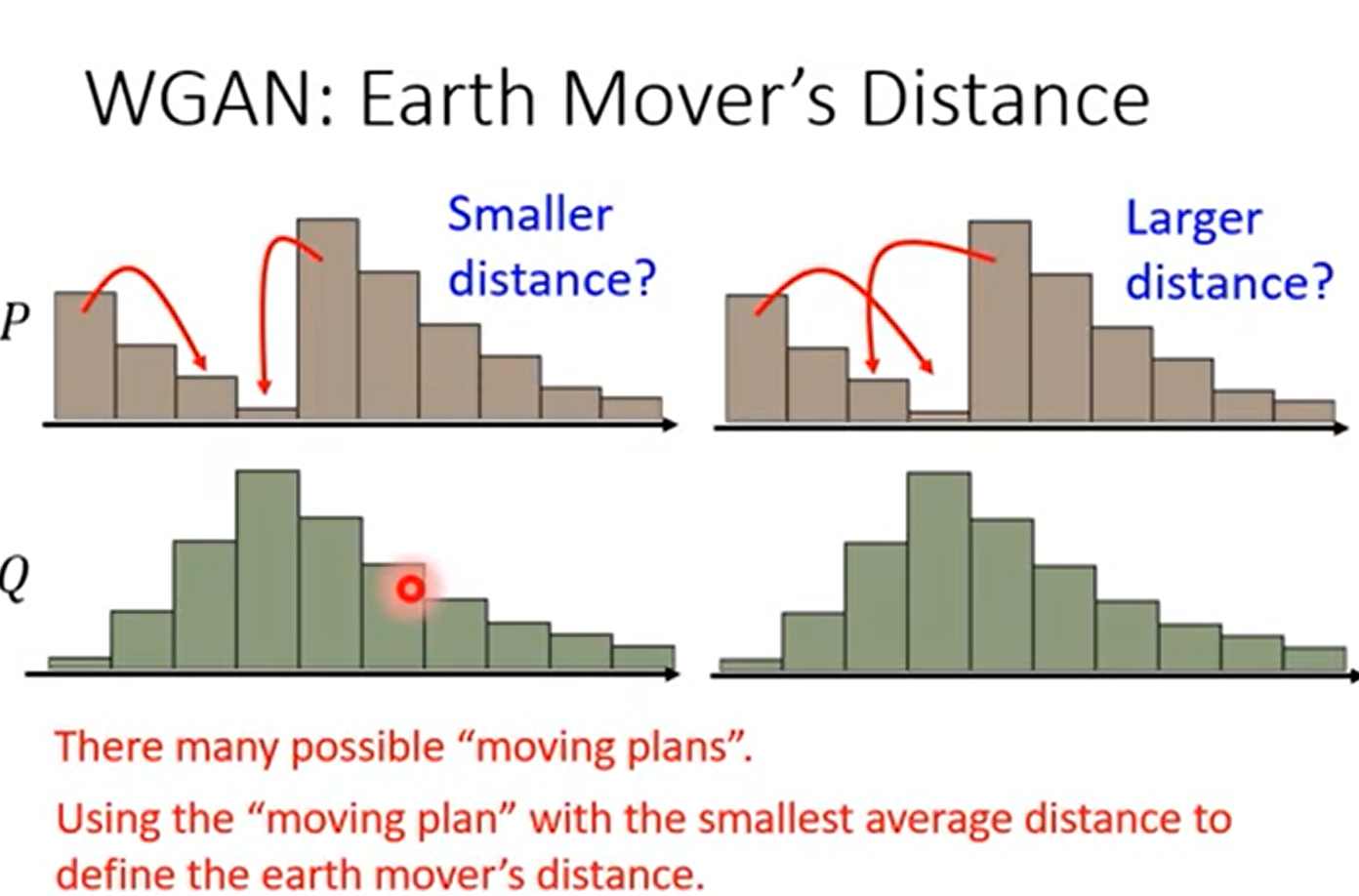
我们想将一个分布移动到另一个分布，可以把分布想象称为土堆，我们每次取样，进行移动。这个过程像是推土机或者说挖掘机移动土堆，我们每次移动一点，最终把整个土堆移动完成，或者说是把土堆填到沟里。如果是离散的分布，那就是每次移动一个有质量的点。(实际上Wasserstein距离就是在最优路径下搬运过程的最小消耗，又被称作Earth-Mover Distance)

在一维分布时，很形象

但在二维上面，事实上有很多种方法，推土机距离就是定义为穷举所有的方案，距离最小的那个

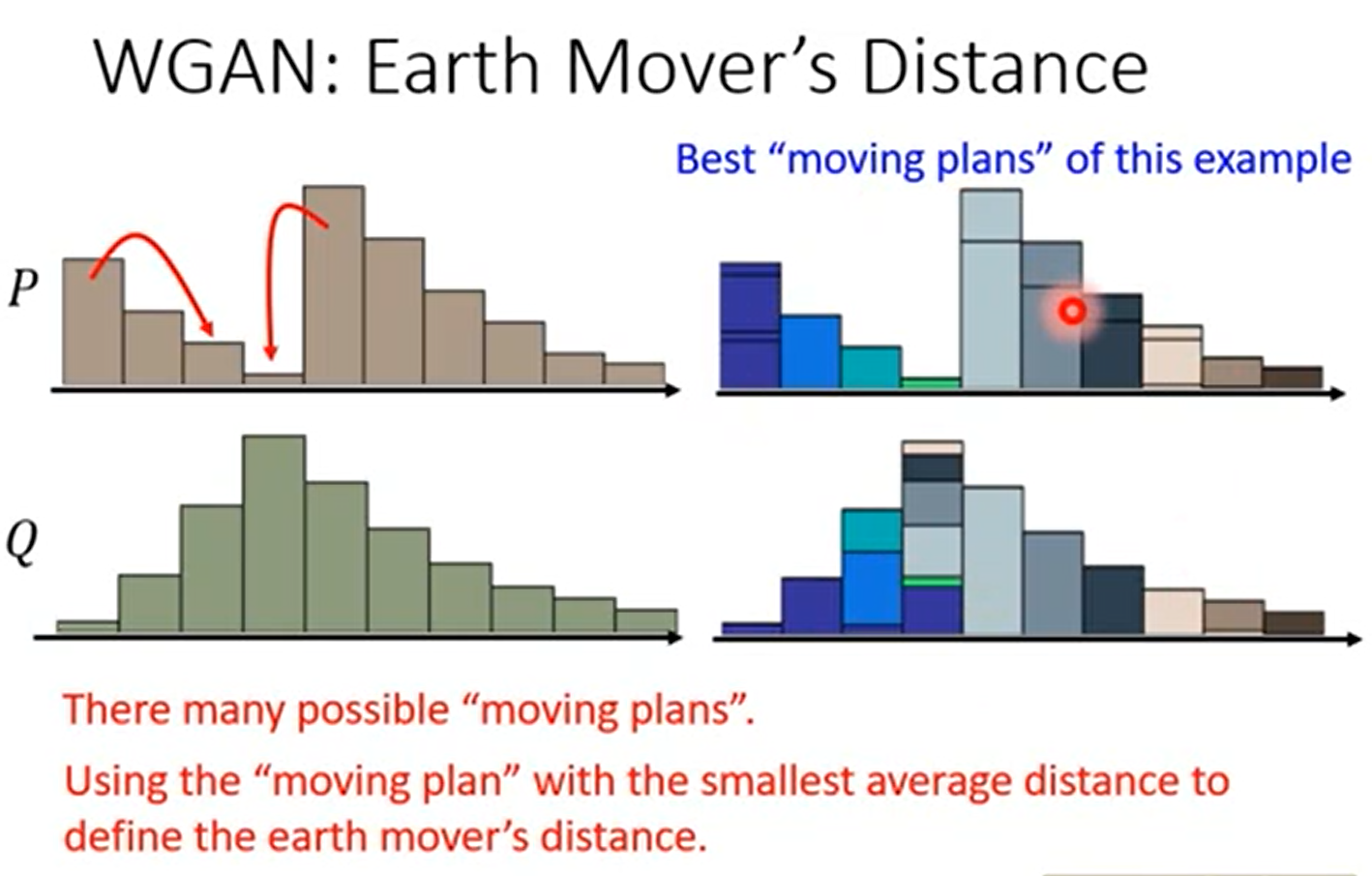
正式定义

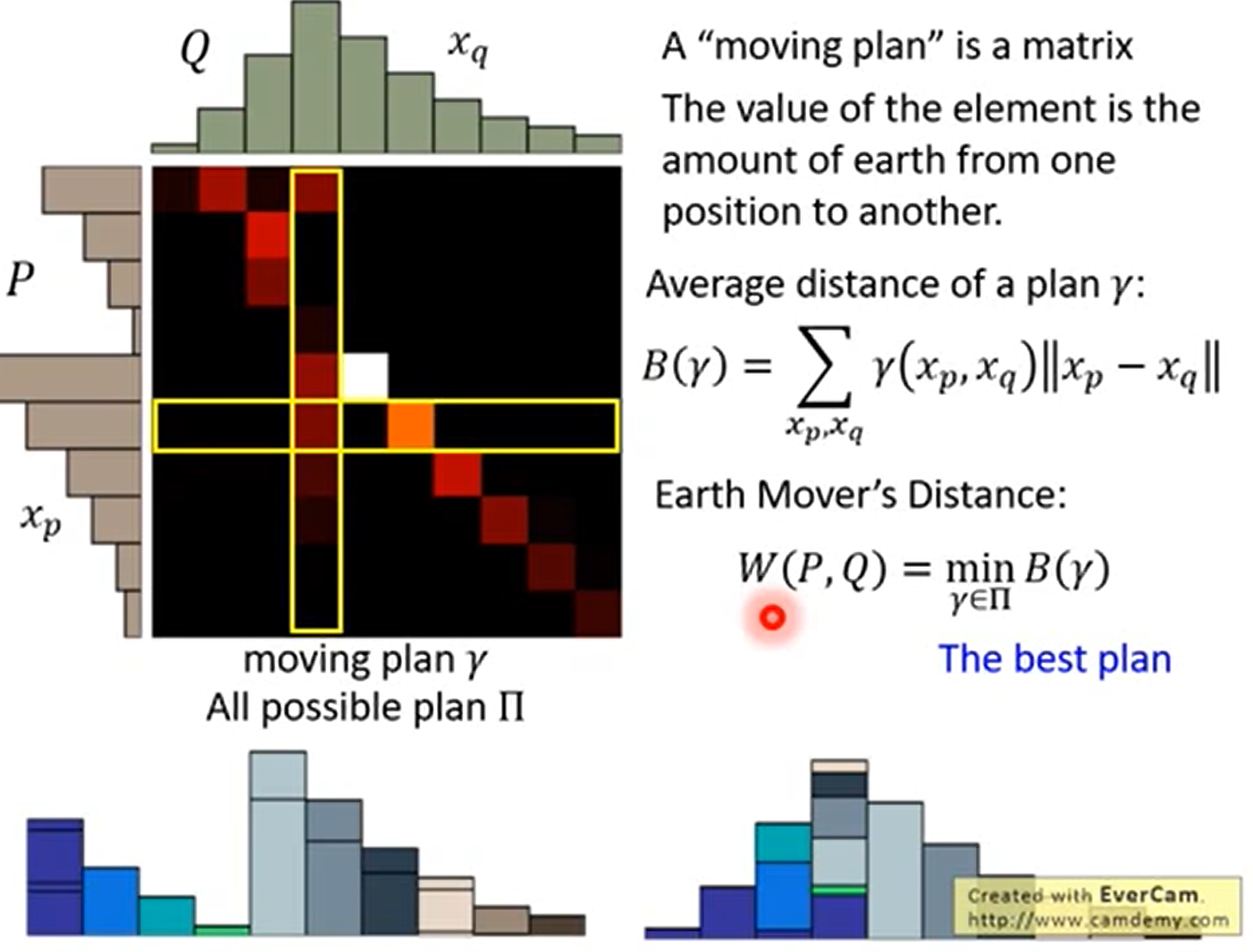
这里实际上是在所有的方案中，选择最小的那个方案得到的距离。

Earth Mover’s Distance 的优点

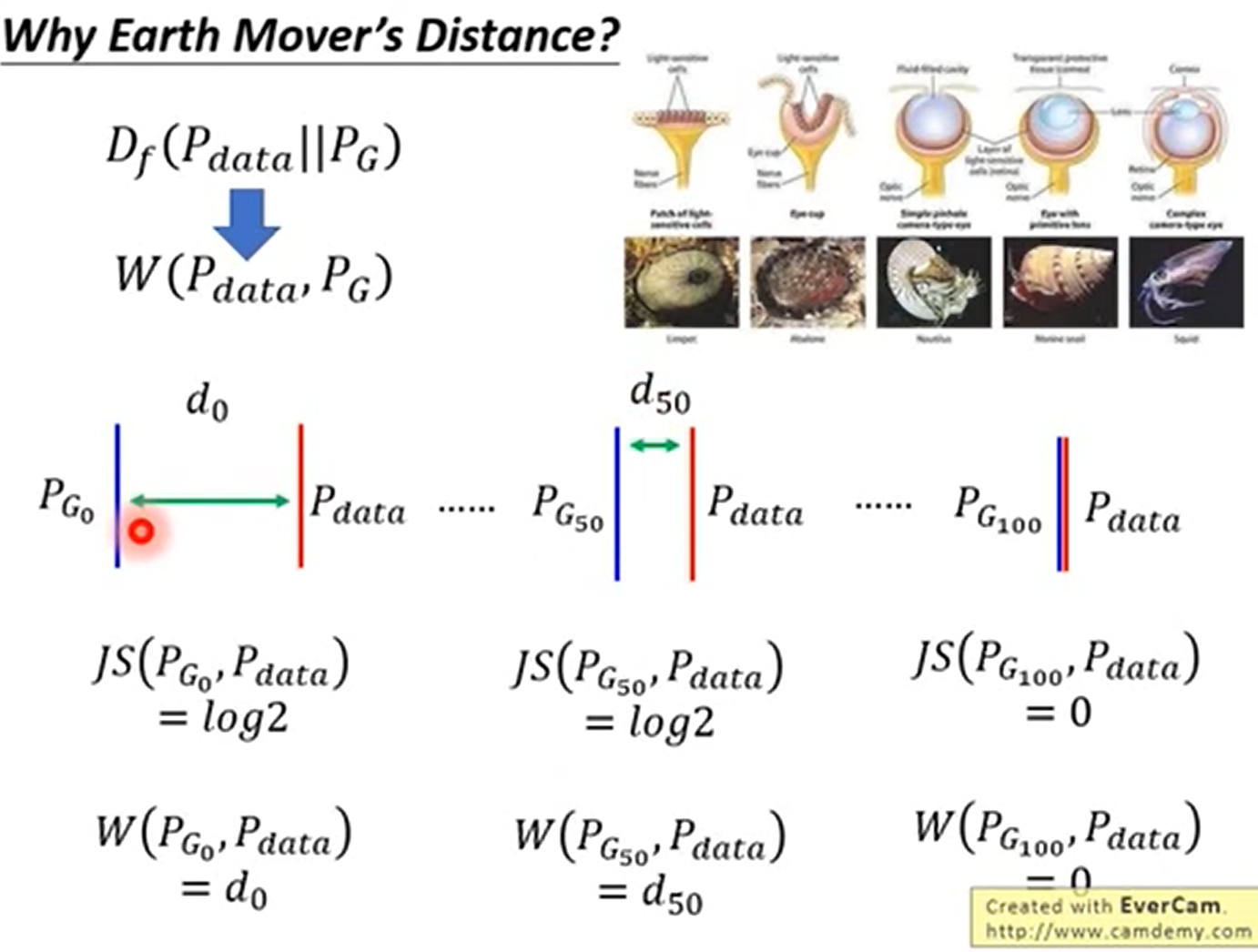
能够衡量不相交的时候的距离，并且距离越近效果越好

Wasserstein距离相比KL散度、JS散度的优越性在于，即便两个分布没有重叠，Wasserstein距离仍然能够反映它们的远近；而JS散度在此情况下是常量，KL散度可能无意义

考虑如下二维空间中的两个分布$P_1$和$P_2$，$P_1$在线段AB上均匀分布，$P_2$在线段CD上均匀分布，通过控制参数$\theta$可以控制着两个分布的距离远近。

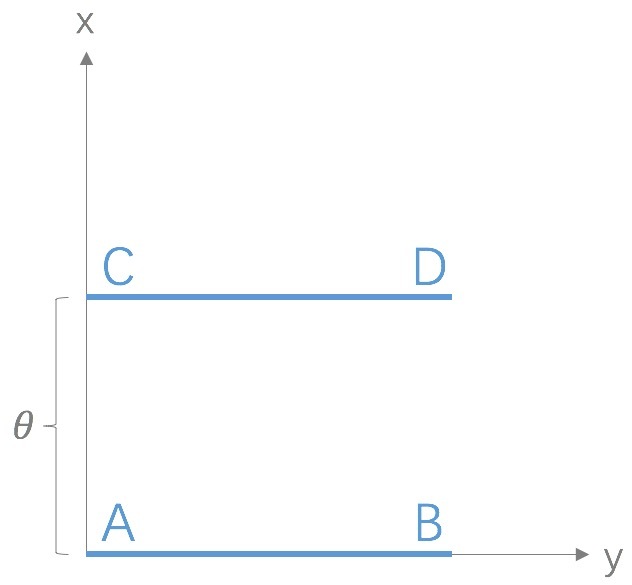
此时容易得到

（突变)

（突变）

（平滑）

KL散度和JS散度是突变的，要么最大要么最小，Wasserstein距离却是平滑的，如果我们要用梯度下降法优化这个参数，前两者根本提供不了梯度，Wasserstein距离却可以。类似地，在高维空间中如果两个分布不重叠或者重叠部分可忽略，则KL和JS既反映不了远近，也提供不了梯度，但是Wasserstein却可以提供有意义的梯度。

感谢

“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”、“交叉熵”_哔哩哔哩_bilibili