最小二乘法
1 几何直观角度—距离和最小
首先,把测试得到的值画在笛卡尔坐标系)中,分别记作$y_i$ :
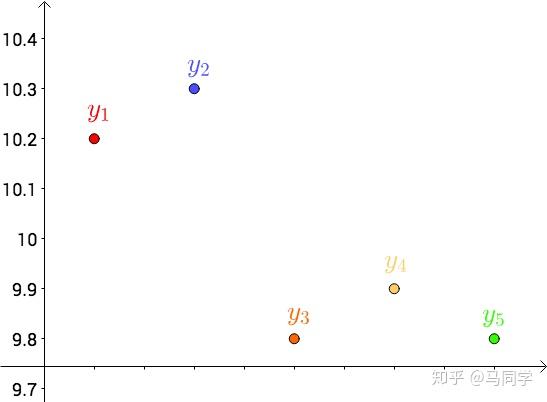
其次,把要猜测的线段长度的真实值用平行于横轴的直线来表示(因为是猜测的,所以用虚线来画),记作$y$ :
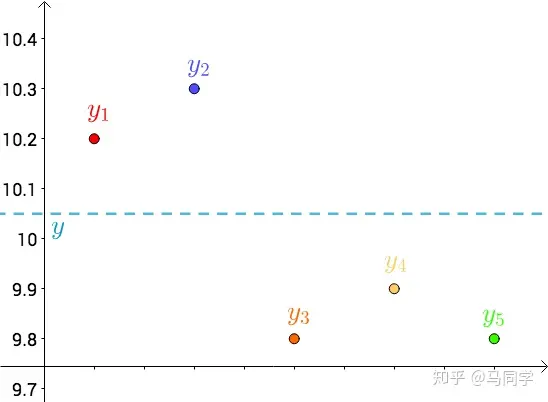
| 每个点都向$y$做垂线,垂线的长度就是$ | y - y_{i} | $ ,也可以理解为测量值和真实值之间的误差: |
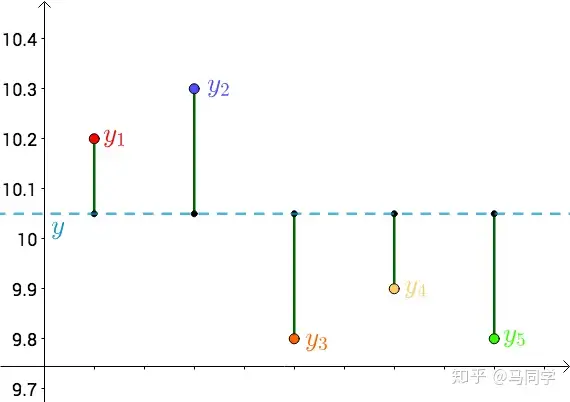
因为误差是长度,还要取绝对值,计算起来麻烦,就干脆用平方来代表误差: \(|y-y_i|→(y-y_i)^2\)
误差的平方和就是($\epsilon$代表误差) : \(S_{\epsilon^2} = \sum(y-y_i)^2\) 因为$y$是猜测的,所以可以不断变换:
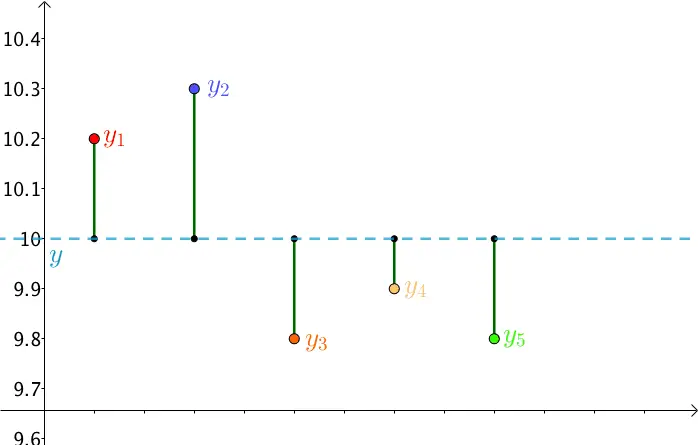
自然,误差的平方和$S_{\epsilon^2}$在不断变化的。
法国数学家,阿德里安.马里.勒让德 ( 1752 - 1833 )提出让总的误差的平方最小的y就是真值,这是基于,如果误差是随机的,应该围绕真值上下波动。
勒让德的想法变成代数式就是: \(S_{\epsilon^2} = \sum(y-y_i)^2 最小 \rightarrow 真值 y\)
2 几何角度 ——投影

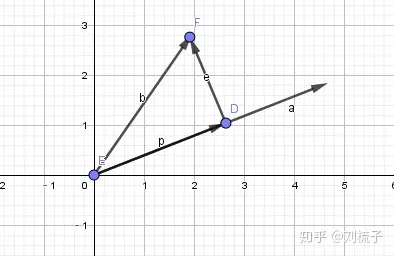
推广到高维情况:
借助矩阵:用矩阵A的列向量空间描述投影空间,向量b为被投影向量!


结论对比前面投影到一个二维向量上的结论,形式完全契合,非常完美!
有了投影矩阵之后,我们来看它的具体应用,其实这就是最小二乘法。

进行投影后,此时残差e的长度最小,e长度最小就对应着最小二乘法的优化目标,因此我们进行投影,得到的近似解,就是最小二乘法的解。
最小二乘法在许多场合都有应用,凡是能抽象出Ax=b的形式,都可以用此方式解决!
3 代数角度——线性方程组的最小二乘解
如果一个方程组无解,那么这个方程组被称为不一致。例如下面的方程组: \(x1+x2=2 \\ x1-x2=1 \\ x1+x2 = 3 \\\) 根据线性代数的知识, $m$个方程$n$个末知量$m > $n时通常无解,但是虽然不能求出$Ax = $b的解,那何不退而求其次,寻找与解近似的向量$x$。 那么如何定义与解相似, 一般使用欧氏距离来进行度量,即两点间的距离,这其实很好理解,越相似,欧氏距离越近,这样求出的$x$被称为最小二乘解。
| 线性方程组$Ax = b$的最小二乘解通过最小化余项的欧几里得范数$ | Ax - b | ^2$ ,可以通过法线方程或QR分解来求出最小二乘解。 |
法线方程
将我们开始举的例子写成矩阵形式: \(\left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} x_1 \\ x_2 \end{array}\right]=\left[\begin{array}{l} 2 \\ 1 \\ 3 \end{array}\right]\) 写成等价方程为 : \(x_1\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]+x_2\left[\begin{array}{c} 1 \\ -1 \\ 1 \end{array}\right]=\left[\begin{array}{l} 2 \\ 1 \\ 3 \end{array}\right]\) 对于任意 $m \times n$ 方程组 $A x=b$ 都可以看做向量方程 : \(x_1 v_1+x_2 v_2+\cdots+x_n v_n=b\) 其实也就是把 $b$ 看做 $A$ 的列向量的线性组合 $\mathrm{Q}$ ,对应的系数即为 $x_i$ ,对于举的例子来说,就是把 $b$ 表示为另外两个三维向量的线性组合,由于 $R^3$ 中两个三维向量的组合生成一个平面,方程仅当 $\mathrm{b}$ 在这个平面上才有解,推广至 $\mathrm{m}$ 个方程 $\mathrm{n}$ 个未知量 $m>n$ 时也是相同的情况。
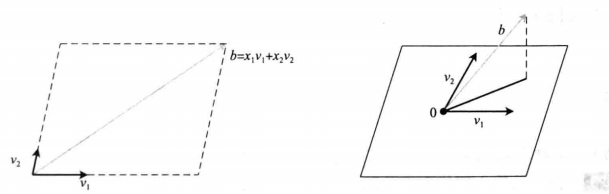
上图表明了如果解不存在时的情况,
如果对于例子没有点$x_1\(, x_2$满足条件,但是在所有候选点构成的平面$Ax$中与$b$最接近的点,即有一个向量$A\bar{x}$满足$b-A\bar{x}$与平面${Ax|x\in^n}$垂 直,那么表达成数学语言就是向之间正交,即:\) (Ax)^T(b- Ax)=0 \(运算一下,就有:\) x^T A^T(b- Ax)= 0 \(也就是$n$维向量$A^T(b - A\bar{x})$和$R^n$包括自己在内的其他$n$维向睡直,那么满足条件的只有$0$ 向量,即:\) A^T(b- A\bar{x})= 0
A^T A\bar{x}= A^Tb $$ $A^T A\bar{x}= A^Tb$就被称为法线方程,它的解$\bar{x}$也就是方程组$Ax = b$的最小二乘解。
QR分解
通过QR分解实现最小二乘的算法为: 给定 $m \times n$ 不一致系统 \(A x=b\) 找出完全 $Q R$ 分解 $A=Q R$, 令 \(\begin{aligned} & \hat{R}=R \text { 的上 } n \times n \text { 子矩阵 } \\ & \hat{d}=d=Q^T b \text { 的上面的 } n \text { 个元素 } \end{aligned}\) 求解 $\hat{R} \bar{x}=\hat{d}$ 得到最小二乘解 $\bar{x}$ $\mathrm{QR}$ 分解可以通过不计算 $A^T A$ 来避开最小二乘法线方程方法带来的病态问题,
4 概率角度——噪声服从正态分布的最大似然估计
用 $F(y \mid x)$ 表示当 $x$ 取到一个确定值时,所对应的 $Y$ 的分布函数。
$Y$ 的期望 $E(Y)$ 随 $x$ 取值而定,是一个关于 $x$ 的函数,我们将其记为 $\mu(x)$ ,称为 $Y$ 关于 $x$ 的回归函数。
若 $\mu(x)$ 为线性函数 : $\mu(x)=a x+b$ ,若误差服从正态分布,即 $\epsilon \sim N\left(0, \sigma^2\right)$ ,那么 相当于: \(Y=a x+b+\epsilon, \epsilon \sim N\left(0, \sigma^2\right)\) $\epsilon$ 是随机误差,人们不可控制的。此时 $Y \sim N\left(a x+b, \sigma^2\right) , Y$ 也服从正态分布。 要估计参数 $a, b$ ,可借助最大似然估计。
假设有观测数据 $\left(x_1, Y_1\right), \cdots,\left(x_n, Y_n\right)$ ,待估 计参数为 $a, b$ ,则似然函数有: \(L=\prod_{i=1}^n f(y \mid x ; a, b)=\prod_{i=1}^n \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{\left(y_i-a x_i-b\right)^2}{2 \sigma^2}}\) 推得 : \(L=\left(\frac{1}{\sqrt{2 \pi} \sigma}\right)^n e^{-\frac{1}{2 \sigma^2} \sum_{i=1}^n\left(y_i-a x_i-b\right)^2}\) 我们要最大化 $L$ ,其中 $\sigma$ 不依赖于 $x$ ,故最大化 相当于是最小化: \(\sum_{i=1}^n\left(y_i-a x_i-b\right)^2\)
诶妈呀这不就是最小二乘法吗,所以在线性回归中,若误差服从正态分布 (或 服从正态分布), 则最小二乘法就是极大似然估计!
4 概率角度——指数分布族 GLM
判断标准非常简单,响应变量y独立则GLM,否则GLMM。这就是最本质的判断标准,其它的标准都是基于这个标准来的
指数分布族
概率密度为 \(f_X(x;\theta) = h(x) e^{ (\ \eta(\theta)\cdot T(x)+A(\theta)\ )}\)
其中
$\eta(\theta)$被称为这个分布的自然参数(natural parameter )
$T(x)$为充分统计量(sufficient statistic) ,通常 $T(x)=x$
$A(\theta)$为累计函数(cumulant function) , 作用是确保概率和$\sum f(x;\theta)$为1
$h(x)$为 underlying measure
当 $T,A,h(y)$固定之后就确定了指数分布族中的一种分布模型,就得到了以$\eta$为参数的模型
还有两个等价的形式 \(f_X(x|\theta) = h(x) g(\theta) e^{(\ \eta(\theta)\cdot T(x) \ )} \\ f_X(x|\theta) = e^{(\ \eta(\theta)\cdot T(x)+ A(\theta) \ )}\)
其实,大多数概率分布都属于指数分布族:
伯努利分布(Bernouli):对0,1问题进行建模
二项分布(Multinomial): 对K个离散结果的事件建模
泊松分布(Poisson)
指数分布(exponential)和伽马分布(gamma):
高斯分布(Gaussian)
$\cdots$
假设
为了给问题构造GLM模型,必须首先知道GLM模型的三个假设
$y x;\eta \thicksim ExponentialFamily(\eta)$ .
比如给定样本$x$与参数$\eta$,样本的分类$y$服从以$\eta$为参数的指数分布族中的某个分布
给定$x$,广义线性模型的目标是求解$T(y) x$ 来预测$T(y)$的期望, 即给定样本$x$的分类 。
不过由于很多情况下$T(y)=y$,所以我们的目标就变成了$h(x)=E[y x;\theta]$。即给定样本$x$估计的目标就是输出$E[T(y) x]=E[y x]$。 - $\eta=\theta^T x$ .
即自然参数$\eta(\theta)$和输入$x$满足线性关系,第3条“假设”更应该被视为一种“设计策略”,来简化模型。
三条假设,第一条是为了能在指数分布范围内讨论y的概率,第二条假设是为了使得预测值服从均值为实际值得一个分布,第三条假设是为了设计的决策函数(模型)是线性的。
最终的模型是依赖于模型服从什么样的分布,比如 高斯分布,伯努利分布。
高斯分布与最小二乘
在线性回归中,我们对概率分布做出的假设是服从正态分布 $y x;\theta \thicksim N(\mu,\delta^2) $ 我们可以将$\delta$设为1 ,那么则服从$y x;\theta \thicksim N(\mu,1) $
由上面推导,我们可以得知 \(p(y;\mu) = \frac{1}{\sqrt{(2 \pi)}} exp(-\frac{1}{2}(y-\mu)^2) \\ =\frac{1}{\sqrt{(2 \pi)}} exp(-\frac{1}{2}y^2)exp(\mu y-\frac{1}{2}\mu^2 )\)
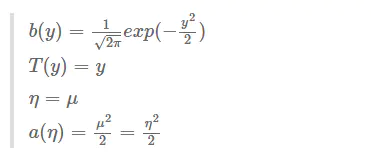
- 根据第三个假设 $\eta=\theta^T x$
于是我们就有
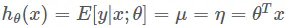
线性回归下最大似然估计与最小二乘的统一
我们发现对高斯分布做最大似然估计
.jpg)
4 概率角度——贝叶斯推断
我们可以将$P(\theta |X)$进行贝叶斯概率进行展开 \(P(\theta | X) = \frac{ P(X| \theta)}{ P(X)} \cdot P(\theta) \ \ \ (2)\) 上式中$ P (\theta|X)$称作后验概率 , $P(\theta)$称作先验概率。$P(X|\theta)$叫做似然度,$P(X)$是边缘概率,与待估计参数$\theta$无关,又叫做配分函数
我们知道似然函数$L(\theta|X)$等于在固有属性$\theta$ 下 $X$的发生概率 $P(X|\theta)$ ,将其带入(2),得到 \(P(\theta | X) = \frac{ L( \theta |X )}{ P(X)} \cdot P(\theta) \ \ \ (3)\) 在上式中,$L(\theta | X)$ 称为 似然度。在上式中,我们要求的就是$\theta$ ,不妨将其记为一个关于$\theta$的函数$f_x(\theta)$
\(f_x(\theta) := P(\theta | X) = \frac{ L( \theta |X )}{ P(X)} \cdot P(\theta)\) 和上面类似我们是想求$\theta$ , 我们使用$f_x(\theta)$取得最大值时的$\theta$来代替。我们可以观察式子的右端,分母$P(X)$是与$\theta$无关的,我们想要求最大值,只需求$L(\theta|X) \cdot P(\theta)$的最大值即可。也就得到了我们的最大后延估计MAP


$ P(w)$是先验概率,也就是我们根据经验对于可能的分布的一个猜测。
可以看到,当假设分布服从常数分布时,$ logP(w)$是一个常数,可以忽略不计,最大后验估计退化为最大似然估计。还有就是我们不认为存在先验概率时,最大后验估计退化为最大似然估计。
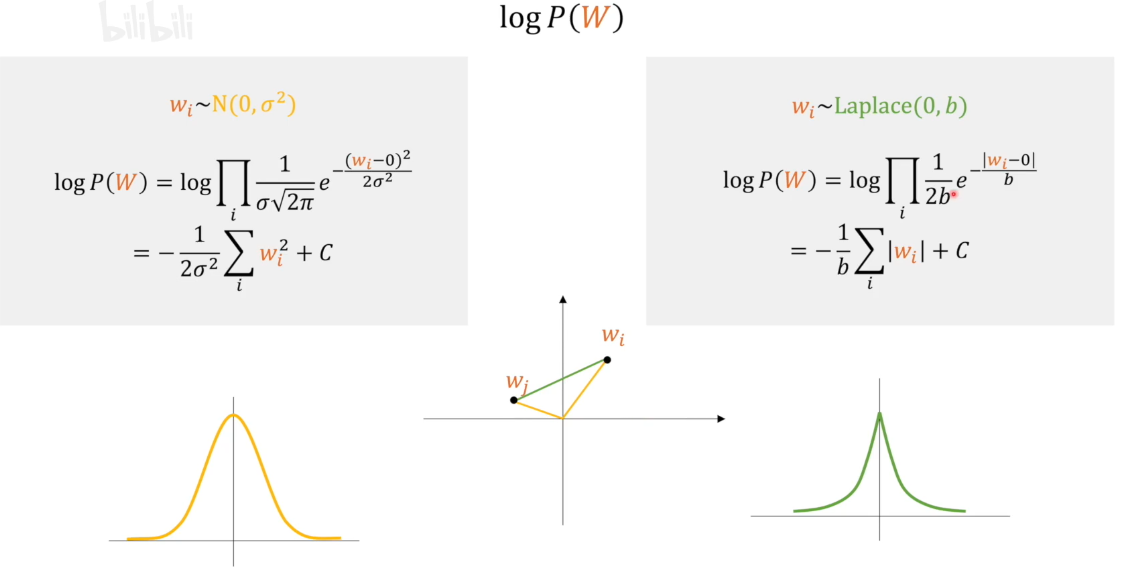
当假设分布服从正态分布和拉普拉斯分布,分别得到L2正则化项和L1正则化项
文档信息
- 本文作者:zuti666
- 本文链接:https://zuti666.github.io/2023/10/11/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)