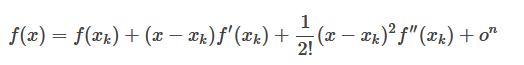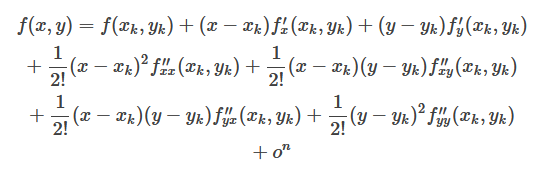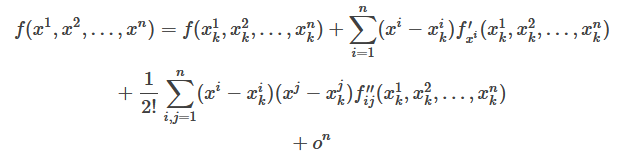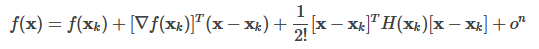Paper Reading Note1—Learning a Similarity Metric Discriminatively with Application to Face Verification 2005

参考博客

Learning a Similarity Metric Discriminatively, with Application to Face Verification.-CSDN博客

【CV论文笔记】Learning a Similarity Metric Discriminatively, with Application to Face Verification - 简书 (jianshu.com)

AI 总结

文章的主要内容：

领域与问题设置：

这篇文章的研究领域是面部验证及广泛的识别任务，尤其是类别数量非常大且训练时未知的情况下。传统的分类方法依赖于已知类别并需要大量数据进行训练，但该文提出的问题是，当类别众多且样本较少时，如何通过学习相似度度量来应对识别与验证任务。

核心思想：

文章的核心思想是通过判别性学习方法训练相似度度量，这种度量可以在训练后用于比较新类别样本。该方法使用Siamese（孪生）网络结构，旨在将输入模式映射到一个低维目标空间，使得该空间中的简单距离（如欧氏距离）能够近似输入空间中的“语义”距离。具体而言，该系统通过训练来确保相同类别的样本对的相似度较高（距离较小），而不同类别的样本对相似度较低（距离较大）。

主要方法：

1. Siamese网络结构：使用两套相同的卷积网络处理输入的两张图像，并通过共同的参数更新，学习出图像之间的相似性度量。
2. 判别性损失函数：为了防止模型崩溃（即所有输入对的损失为零），提出了一个对比性损失函数，确保来自相同类别的样本对的能量低，来自不同类别的样本对的能量高。
3. 卷积网络：利用卷积网络来处理输入的图像，这种网络在应对几何扭曲（如位移、缩放、旋转）时表现出色，能够学习出对图像不变的特征。

与其他方法的区别：

• 传统方法（如PCA、LDA等）依赖线性投影并不具备良好的几何扭曲鲁棒性，且通常在类别数量有限的条件下应用。
• 基于生成模型的非判别性方法通常依赖于简化的概率模型，这些模型要求在训练时为每个类别提供样本。
• 本方法的创新点在于不依赖先验知识来设计不变性，而是通过卷积网络从数据中学习不变性，且这种方法能够处理未在训练中见过的新类别样本。

优点：

• 处理大规模类别问题：该方法适合于处理类别非常多的任务，并且能够处理训练时类别未完全已知的情况。
• 鲁棒性强：由于使用了卷积网络，该模型能够处理几何变换、表情变化以及部分遮挡等带来的挑战。
• 可扩展性好：相似度度量学习完成后，系统可以应用于识别训练集中未见过的类别，这使得该模型非常适合应用于实际的面部验证任务。

总结起来，这篇论文提出了一种创新的判别性相似度度量学习方法，特别适用于处理类别众多且训练数据有限的识别任务，尤其在面部验证领域表现突出。

算法的证明

在文章的算法证明部分，作者提出了三个条件，这些条件用于确保所设计的损失函数在优化过程中能够引导模型朝向正确的相似性度量。以下是对这三个条件的概括总结：

1. 条件1（Margin条件）：
   • 描述：这个条件要求模型能够正确区分相同类别的样本对和不同类别的样本对。具体而言，对于相同类别的样本对，模型计算出的能量应当低于不同类别样本对的能量，并且两者之间的差距必须超过一个预设的正数“margin”。
   • 作用：该条件确保模型在训练过程中不仅仅缩小同类别样本的能量，还扩大不同类别样本的能量差异，避免能量过于接近。
2. 条件2（损失函数的最小值位置）：
   • 描述：损失函数的最小值应该位于能量差大于零的区域内。也就是说，当相同类别样本的能量低于不同类别样本的能量时，损失函数才会取得最小值。
   • 作用：这个条件保证了在优化过程中，模型能够通过减少相同类别样本的能量和增加不同类别样本的能量来正确分类，而不是通过简单地降低所有能量值来最小化损失。
3. 条件3（损失函数梯度方向）：
   • 描述：在条件2所描述的“margin线”上，损失函数的梯度方向必须指向能量差大于零的区域。换句话说，损失函数的优化过程应该促使能量差变大，确保相同类别样本对的能量降低，不同类别样本对的能量升高。
   • 作用：该条件确保梯度下降法能够朝着减少损失的正确方向移动，从而避免模型停留在次优解上。

总结来说，这三个条件共同作用，确保模型在训练过程中能够正确地优化相似度度量，区分相同类别和不同类别的样本对，最终实现可靠的面部验证算法。

文章精读

Abstract

核心的想法：

The idea is to learn a function that maps input patterns into a target space such that the norm in the target space approximates the “semantic” distance in the input space.”

基本的思路：

that drives the similarity metric to be small for pairs of faces from the same person, and large for pairs from different persons.

映射的函数：

The mapping from raw to the target space is a convolutional network

数据集：

the Purdue/AR face database

Intro

motivation

传统的分类方法是判别式的，需要

“generally require that all the categories be known in advance. They also require that training examples be available for all the categories.”

“where the number of categories is very large, where the number of samples per category is small, and where only a subset of the categories is known at the time of training.”

(1) 训练的时候知道所有的类 (2) 每个类的训练样本可用，并且越多越好这限制了一些场景下的使用，例如面部验证和面部识别，其中每个人看成一个类。还有一种情况就是即使不是在实际应用中，而是一些用于科研数据集 (dataset) 所包含的类也是特别多的，并且很有可能每个类都只有很少的样本可用于训练。

文章提出了一种从数据中训练相似性度量的方法。这种方法适用于识别和验证任务，其中任务特点：

1 number of categories is very large 2 number of samples per category is small 3 only a subset of the categories is known at the time of training

（1）数据所属的类别特别多 （2）有些类别在训练的时候是未知的 （3）并且每个类别的训练样本特别少。

ps: 这三个特点和 meta-learning（元学习）的特征是一致的。 （1）数据所属的类别多（虽然有些类别训练时是未知的），可以帮助 meta-learning 从这些类别中学习到可以用于处理新类的先验知识 (prior)； （2）有些类别训练的时候未知，这和 meta-learning 想做的可以把学到的先验知识用在新的任务上的本质思想是一致的。 （3）每个类别的训练样本特别少，这是一种典型的 few-shot learning 设置。也是 meta-learning 在监督情景下的解决的典型问题。

other method difference

一种常见的解决方法是基于距离 (distance-based) 的方法，方法包含需要分类或验证的模式之间的相似性度量以及一个存储的原型库。

“distance-based methods, which consist in computing a similarity metric between the pattern to be classified or verified and a library of stored prototypes.”

另一种解决方法是在降维空间里使用一种非判别的（生成式）概率方法，这种方法训练一个类时，不需要其他类的样本。

Another common approach is to use non-discriminative (generative probabilistic methods in a reduced-dimension space, where the model for one category can be trained without using examples from other categories.

本文提出了一种从训练数据中学习相似性度量的方法，并且这个相似性度量可以用于比较来自训练时没有见过的新的类的样本（例如，一个新人的面部图片）。这种方法是判别式的，可以用于分类问题，其中类别数很多 and/or 每个类别的样本很少。

this paper focus

“To apply discriminative learning techniques to this kind of application, we must devise a method that can extract information about the problem from the available data, without requiring specific information about the categories.”

core idea 核心思想

“learn a similarity metric from data” (Chopra 等, 2005, p. 1$

“The main idea is to find a function that maps input patterns into a target space such that a simple distance in the target space (say the Euclidean distance$ approximates the “semantic” distance in the input space.” (Chopra 等, 2005, p. 1$

“siamese architecture” (Chopra 等, 2005, p. 2$

学习一个函数(function)，将输入模式 (input patterns) 映射 (map) 到一个目标空间里面。

并且需要控制这个映射使得目标空间 (traget space) 中的 L1 Norm （相似性度量，similarity metric） 可以近似输入空间 (input space) 中的语义距离，即来自同一人的照片在目标空间中相似性度量小，而来自不同的人的照片相似性度量大。

这和 meta-learning 中的度量学习 (metric learning) 本质思想完全一致，只是相似性度量的选择还有训练时候的策略有差异，度量学习的典型包含 Matching Network, Prototypical networks, Relation Network 等。

Previous Work

“PCA-based Eigenface method [16]” (Chopra 等, 2005, p. 2$

“LDA-based Fisherface method [3]” (Chopra 等, 2005, p. 2$

“to maximize the ratio of inter-class and intra-class variances.” (Chopra 等, 2005, p. 2$

One major shortcoming of all those approaches is that they are very sensitive to geometric transformations of the input images (shift, scaling, rotation and to other variabilities (changes in facial expression, glasses, and obscuring scarves

“Tangent Distance method [19]” (Chopra 等, 2005, p. 2$

“elastic matching [6].” (Chopra 等, 2005, p. 2$

advantage

“In the method described in this paper, the invariance properties do not come from prior knowledge about the task, but they are learned from data.” (Chopra 等, 2005, p. 2$

energy-based models (EBM)

“The advantage of EBMs over traditional probabilistic models, particularly generative models, is that there is no need for estimating normalized probability distributions over the input space.” (Chopra 等, 2005, p. 2$

The General Framework

The energy function of the EBM

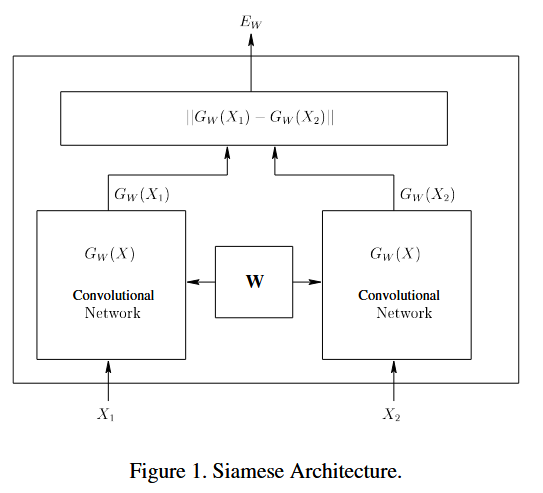
假设$X_1$和$X_2$就是我们的一组输入图片，$Y$就是一个二分类的标签，如果这组图片相似（属于同一个人）则为1，如果不相似则为0。然后$W$就是共享的参数，$G_w(X_1)$ 和 $G_w(X_2)$就是映射后的特征值，则我们可以定义一个标量“能量方程（energy function)”，

给予2组图片，其中一组是相似的，一组是不相似的，我们需要如果 $X_{1}$，$X_{2}$是同一人照片，那么 $E_{W}\left(X_{1}, X_{2}\right)$小，反之来自不同人，则相似性度量大。 注意，这是相似性度量，不是相似性。所以其实是这个相似性度量小，相似性越大。 训练思想：训练集为成对的模式，即

其中$X_{1}$ 和 $X_{2}$是需要验证图片： （1）如果$X_{1}$和 $X_{2}$来自同一人，最小化相似性度量。 （2）如果$X_{1}$和 $X_{2}$来自不同人，最大化相似性度量。 对映射函数$ G_{W}(X)$的唯一要求是对参数 $W$可微。

因为对两个图片使用的是同一个映射函数（参数共享），因此属于Siamese架构。个人觉得这个和后面介绍的 Siamese Network（用于One-shot 图像识别）异曲同工。

需要再次强调，这个映射函数$G_{W}(X)$的选择是自由的，但是对于图像问题，一般会选择卷积神经(CNN) 。

损失函数 一个直接的想法是使用来自同一人的图片对 $\left(X_{1}, X_{2}\right)$来最小化$E_{W}\left(X_{1}, X_{2}\right)$。但是这回遇到灾难性的崩溃。 例如，可能会让 $ G_{W}(X)$ 等于一个常量，这样$E_{W}\left(X_{1}, X_{2}\right) = 0$最小恒成立，但是对于不同对来说，他们的$E_{W}\left(X_{1}, X_{2}\right)$ 还是为 0 。根本无法区分！！！

因此选择对比项作为损失函数，不仅使来自同一人的图片对的相似性度量小，并且来自不同人的相似性度量大。

相同人的图片对$\left(X_{1}, X_{2}\right)$有一个二进制标记 $Y=0$ 不同人的图片对 $\left(X_{1}, X_{2}^{\prime}\right)$ 具有一个二进制标记 $Y=1$

当然要使我们的模型可以按照理想方法训练必须满足：

这很容易理解，必须不同对的相似性度量大于相同对的相似性度量，m 是一个正数，我们称为边际。为了简化，我们将 $E_{W}\left(X_{1}, X_{2}\right)$ 简化为 $ E_{W}^{G}$ ( I = ‘genuine’ ) , $ E\left(X_{1}, X_{2}^{\prime}\right)$简化为 $E_{W}^{I}$( I = ‘impostor’ )。

因此损失函数为：

其中 $P$为训练对的总数。Y 为二进制标记，$\left(Y, X_{1}, X_{2}\right)^{i}$为第 $i $个样本。$ L_{G}$为相同对的损失函数，$L_{I}$ 为不同对的损失函数。

注意这里是损失函数，而不是相似性度量，他们之间有一个转换关系

实际的损失函数为：

其中 $Q$ 是一个常数，被设为 $E_{W}$的上界。

————————————————

                        版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。 原文链接：https://blog.csdn.net/weixin_37589575/article/details/92582373

————————————————

损失函数的具体推导过程参考原论文 ,大体如下

证明与推导

condition 1

则整套机制应该符合以下的条件(condition 1)，

其中参数$m$就可以被解释为是margin（边缘）

为了简化公式的表达，下文将用$E^G_W$来表示$E_w(X_1, X_2)$和$E^I_W$来表示$E_w(X_1, X^`_2)$。

Contrastive Loss Function used for Training

本文将考虑一组训练样本，包括1对相似的图片$E^G_W$和1对不相似对图片$E^I_W$，定义总的损失函数为

其中$L_G$就是相似组对的损失，$L_I$就是不相似组对的损失。

假设$H$在其两个参数中是凸的（注意：我们不假设关于$W$ ).

还假设存在一个$W$对于单个训练样本，以便满足条件(condition 1)。

condition 2

上式定义的损失函数$H(E^G_W, E^I_W)$的最小值应该在 $E_w(X_1, X_2) + m < E_w(X_1, X^`_2) \tag{1}$的半平面之内。

有了这个条件，那么我们想要寻找损失函数的最小值，只需要关注满足条件1规定的区域即可

但如果 $H$的最小值落在无穷远处，如下图所示

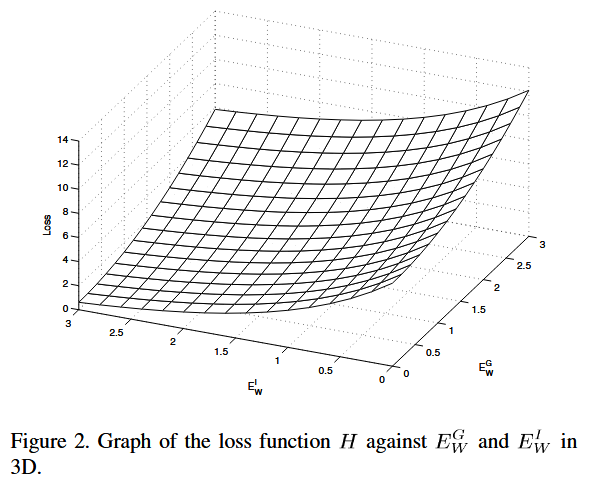
从图中可以看出，随着$E^G_W$和$E^I_W$的减小，函数值Loss不断减小，即为上面提到的情况 $H$落在无穷小处

condition 3

这时候，需要满足以下条件就够了

如果 $H$的最小值落在无穷远处，则需要 $H$在边缘线 $E^G_W+m=E^I_W$上的负梯度有一个带有方向$[-1,1]$的正的点积

接下来只需要证明在这种情况下，最小化$H$的最小值也满足条件1即可。

接下来我们对进行证明。

定理：

令$H(E^G_W, E^I_W) $是关于$E^G_W$和$E^I_W$的凸函数，且在无限远处有最小值。

假设存在一个$W$ ,使得对于采样点满足$E^G_W + m < E^I_W $。

则如果$H$的负梯度在边缘线 $E^G_W+m=E^I_W$有一个带有方向$[-1,1]$的正的点积，那么最小化$H$会导致找到一个满足$E^G_W + m < E^I_W $的$W$。

证明：

考虑由 $E^G_W$和$E^I_W$形成的平面的正象限，如下图所示

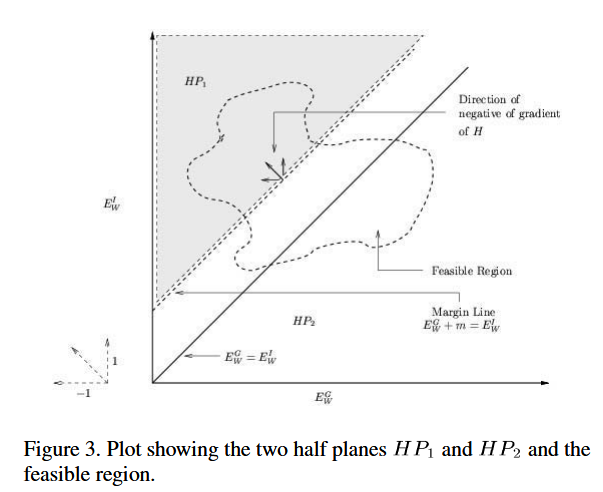
令两个半平面$E^G_W + m < E^I_W $和 $E^G_W + m \geq E^I_W $ 分别表示为 $HP_1$ 和 $HP_2$。

令$R$是由 $E^G_W$和$E^I_W$形组成的平面的内部区域 , 它对应于$W$的所有值。

根据假设，存在一个$W$ ,使得对于采样点满足$E^G_W + m < E^I_W $。这就说明一部分的$R$是与半平面$HP_1$ 相交。

为了根据条件3来证明定理成立，则需要说明 在$R$是与半平面$HP_1$ 相交的区域至少存在一个点，使得损失函数$H$在这个点的值小于 $R$是与半平面$HP_2$ 相交的区域的所有点。

令$E_G^*$是在边缘线$E^G_W+m=E^I_W$上使得$H$最小的一个点，即

有了上述规定以后，在在边缘线$E^G_W+m=E^I_W$上自然有

当$E^G_W+m > E_W^I$ 时，即在平面$HP_2$加上边缘线除$E_G^*$这一个点外，都进一步有

==根据条件3 由于在边缘线上的所有点的 负梯度方向（下降方向）都是指向 $HP_1$平面的== ，即在 $HP_1$的所有点的值的小于对应的边缘线上的值，在 $HP_2$的所有点的值的大于对应的边缘线上的值

现在考虑， 距离边缘线 $E^G_W+m=E^I_W$ 距离为$\epsilon$ ,并且处于半平面$HP_1$的一个点 ，即这个点满足

使用一阶泰勒展开，可以写成下

根据条件3 第二项是一个负值，因此有

因此 在区域$P$ 与半平面$HP_1$的交叉处存在一个点，使得这个点上的损失函数的值比 在区域$P$ 与半平面$HP_2$的交叉处的任何点都小。证明结束。

上述条件三表明：请注意，条件3也显然成立，当无论任何时候$H$,只需满足 $L_0$是单调增函数，$L_1$是单调减函数 。

思考：

上面这几个条件到底时规定了什么，使得最终我们想要的这样的一个 能量函数就是存在的？ 这些假设是否合理以及是否过强？

AI 回答：

这几个条件为能量函数的存在性和可优化性提供了约束，确保通过训练，模型能够学到一个合理的相似性度量。这些条件共同确保了模型可以有效区分同类别和不同类别的样本对，并避免在训练中出现“崩溃”现象（即能量函数趋于无意义的常数值）。具体来说：

这几个条件规定了什么？

1. 条件1：Margin条件
   • 规定了能量差异的目标。这个条件确保相同类别样本对的能量低于不同类别样本对的能量，并且两者之间存在明确的“间隔”（margin）。这使得训练过程不仅仅追求最小化损失函数，还明确了要在样本对之间拉开一定的能量差异。
2. 条件2：损失函数的最小值位置
   • 规定了能量函数最优解的存在性。这个条件确保当相同类别的样本能量低、不同类别的样本能量高时，损失函数可以达到最小值。这意味着模型在合理的相似性度量下能够成功训练出符合条件的能量函数。
3. 条件3：梯度方向条件
   • 规定了损失函数的梯度方向。这个条件确保损失函数的梯度方向指向增大能量差异的区域，避免在优化过程中出现停滞或不收敛的情况。这样就保证了在优化过程中，模型不会陷入次优解，能够有效找到一个符合条件的能量函数。

这些假设是否合理？

• Margin条件（条件1）是合理的。这个条件与许多分类问题中的“间隔最大化”思想类似，确保模型不仅能够区分同类和不同类样本，还能够通过足够的能量差异确保结果稳健，不至于在测试集上出现误差（即相同类别和不同类别样本的能量过于接近）。

• 损失函数的最小值位置（条件2）也是合理的，因为它确保能量函数的最小值只会出现在满足条件的区域，即同类别样本能量低、不同类别样本能量高的区域。否则，如果允许能量过小或过大，模型将无法有效区分不同类别。

• 梯度方向条件（条件3）合理并且是必要的，因为它确保优化算法能够朝正确的方向调整能量函数，避免陷入局部极小值或停滞不前。这类似于很多优化问题中要求的“方向导数条件”，它是确保优化算法有效工作的基础。

假设是否过强？

• 条件1：Margin条件可能在某些实际问题中显得有些严格。例如，某些类别之间的样本相似度本来就非常接近，在这些情况下强行要求一个较大的间隔（margin）可能会导致模型难以收敛。尽管如此，这种margin思想在很多深度学习方法中被广泛使用，且通常通过调整超参数可以缓解其对性能的负面影响。

• 条件2：损失函数的最小值位置不是过强的假设，这是能量函数正确优化的必要条件。如果不满足这个条件，模型无法正确收敛到一个合理的相似性度量。

• 条件3：梯度方向条件是一个标准的优化假设，并不算过强。大多数基于梯度的优化算法（如梯度下降法）都需要此类假设来保证收敛性和可行性，因此这个条件也是必要且合理的。

总结：

这些条件规定了如何在优化过程中保证能量函数的合理性，确保模型学到的相似性度量能够有效区分同类别和不同类别的样本。这些假设整体上是合理的，但margin条件可能在特定场景下显得稍微严格。梯度方向条件和损失函数最小值位置条件是优化问题中的标准假设，并不算过强。

补充知识

补充知识：

一元函数在点$x_k$处的泰勒展开式为：

二元函数在点$(x_k,y_k)$处的泰勒展开式为：

多元函数在点$(x^1,x^2,\cdots,x^n)$处的泰勒展开式为：

把Taylor展开式写成矩阵的形式：

其中