Paper Reading Note2—SDC-ADC-LDC
论文阅读笔记,给大家带来3篇论文的阅读,都是来自LAMP组,三篇文章的思想也都很接近,是基于 特征空间的漂移进行的工作。
首先给出论文信息如下
论文信息
SDC : Semantic Drift Compensation for Class-Incremental Learning CVPR 2020
https://openaccess.thecvf.com/content_CVPR_2020/html/Yu_Semantic_Drift_Compensation_for_Class-Incremental_Learning_CVPR_2020_paper.html
ADC : Resurrecting Old Classes with New Data for Exemplar-Free Continual Learning CVPR2024
https://openaccess.thecvf.com/content/CVPR2024/html/Goswami_Resurrecting_Old_Classes_with_New_Data_for_Exemplar-Free_Continual_Learning_CVPR_2024_paper.html
LDC : Exemplar-free Continual Representation Learning via Learnable Drift Compensation ECCV2024
https://arxiv.org/abs/2407.08536v1
介绍文章的方法之前,我们先来看一下文章的设定是怎样的,介绍一下背景知识。
背景介绍
这篇文章的设定是 continual learning 里的 class-incremental learning
continual learning
对于 continual learning ,基本的设定就是 学习完一个任务之后,神经网络继续学习下一个任务 。但这样的设定会造成一个问题,就是神经网络会遗忘掉之前的知识,导致在之前的任务的能力下降,也就是 灾难性遗忘 Catastrophic forgetting 问题,。continual learning 就是要解决这个 Catastrophic forgetting 问题。
class-increnmental learning
更详细一些, continual learning 里面可以分为三类,分别是 task-increnmental learning , clsaa-incremental learning 和 domian incremental learning ,
首先在 continual learning 的设定中,训练是有顺序的,
就像是上学一样,从一年级到9年纪。不对,这个比喻可能有些偏颇,因为一年级到9年纪的知识是递进的,前面的知识是后面知识的基础,这样的设定就是先学习简单的然后慢慢学习困难的,这种设定一般称之为 课程学习,目的是通过设置训练的次序与内容,最终学会最终的学习目标,学习到最终的任务才是想要的结果。
continual learning 的学习顺序是一个自然的设定,这么设定不是为了学习到最终目标,而是只是表明学习是一个流式的。因为从现实来说,一个人的学习都是被时间限制的,比如今天的我肯定无法学习到10年以后的计算机知识,所以就导致了一个学习任务的顺序。
continual 学习的目的是什么呢,就是今天学了新的知识,但并不能把昨天或之前所学的都忘记了。即不光要求在当前任务做的好,之前的任务也要做的好。这就要求神经网络就不能遗忘掉之前的内容,即要解决灾难性遗忘的问题。
一个顺序学习的简单示意图:
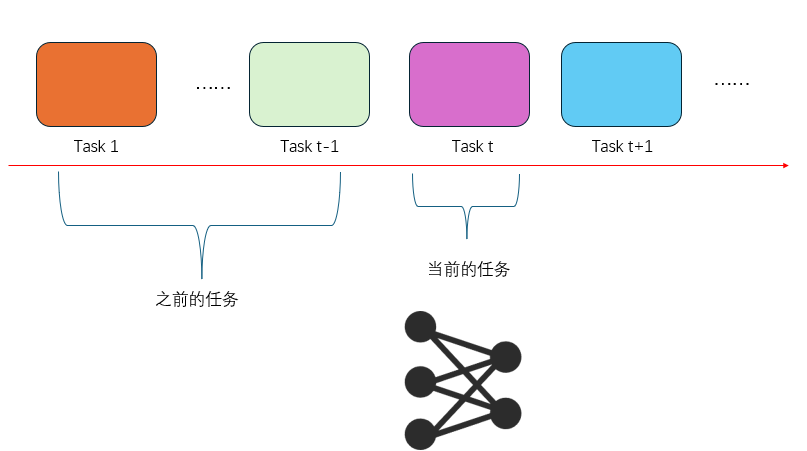
task-incremental learning 的设定很简单,每次的任务不同,但都带有任务的标签。在训练的时候就带有任务的标签,在测试的时候依旧有着任务的标签。
一个现实中的例子就是学习参与不同的运动或者学习不同的乐器,比如一个学生学习先完弹钢琴(task t-1)然后学习吹喇叭(task t)。然后我们想要测试这个学生在之前的任务(弹钢琴)是否还能做得好。那么为了测试,自然得给他一个钢琴。这就相当于是task-incremental learnning的任务标签。
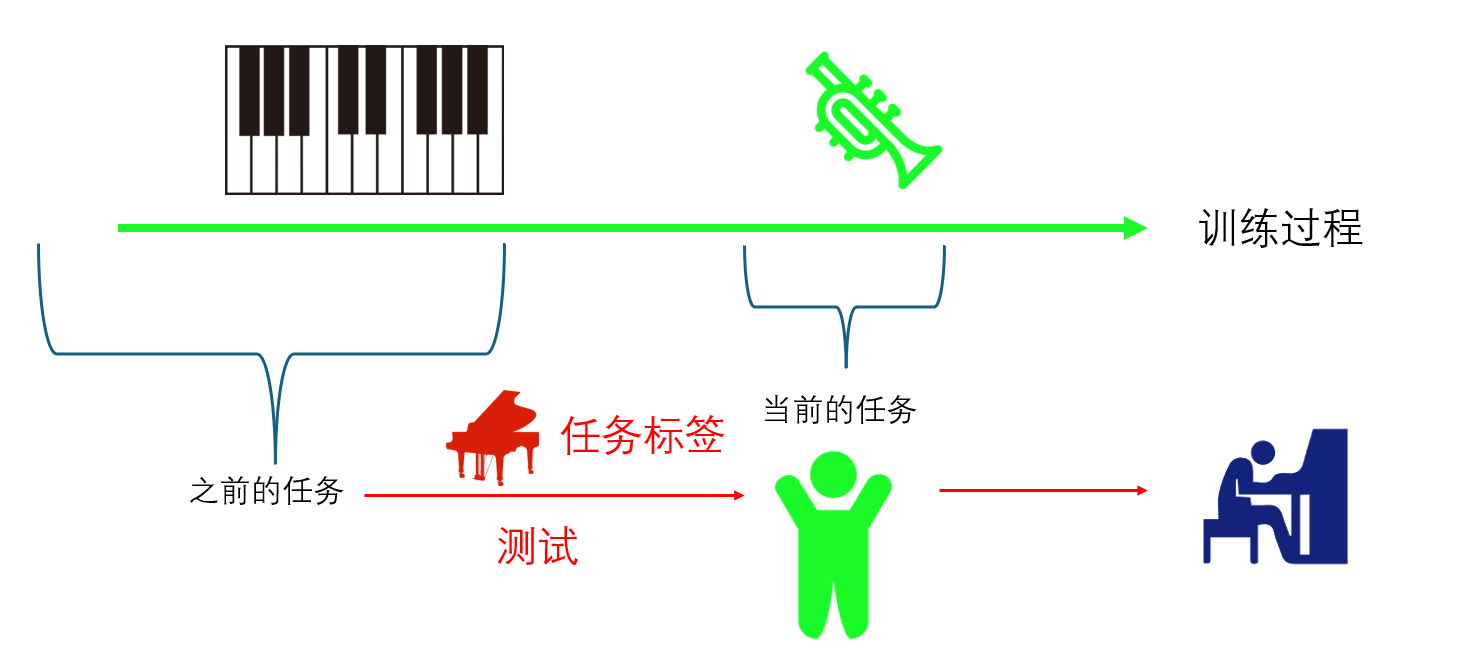
clsaa-incremental learning 的设定是,每次任务不同,且没有任务标签的提示,学习到$t$的时候,之前的所有任务都能做得很好。
举个例子,第一个任务要求区分猫和狗,第二个任务要求区分牛和马。
class-incremental learning 就要求 学习两个任务后,神经网络能够学会识别一个物体,到底是猫或狗或牛或马。
而task-incremental learning 则是告诉神经网络 这是第一个任务,要识别处猫和狗。
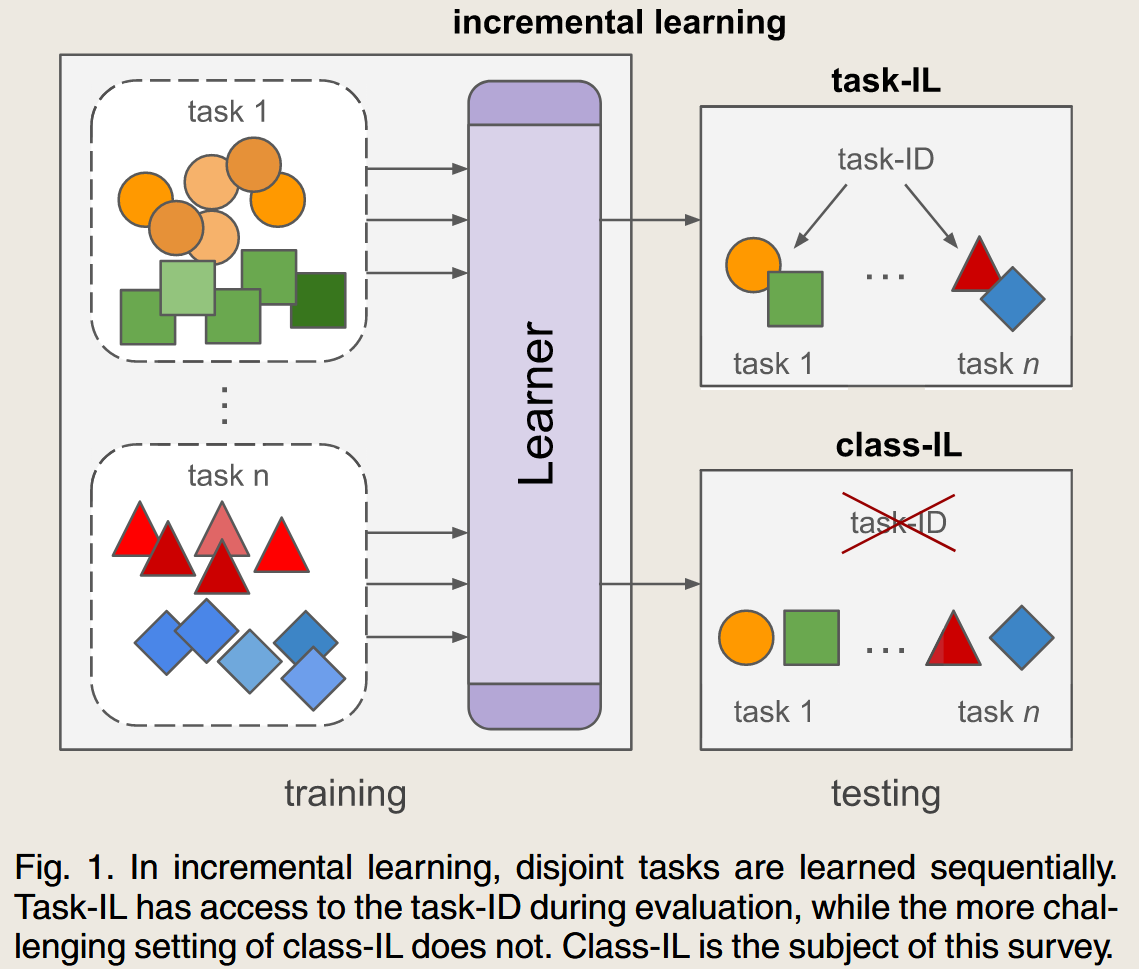
所以显然class-increnmental learning 的要求更符合日常的要求,且难度比task-inremental learning 难得多。两者的区别见下图。
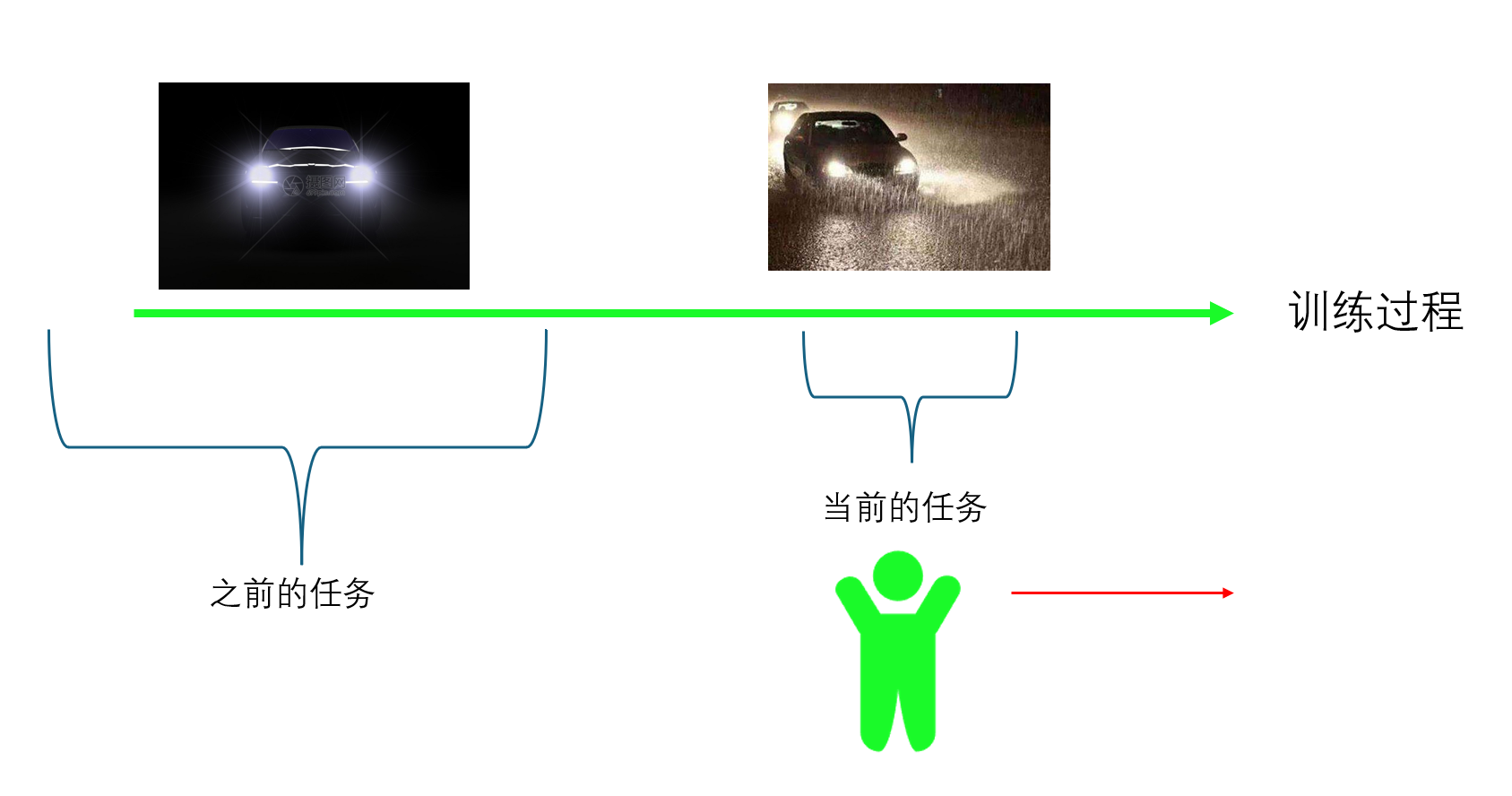
domain-incremental learning 的设定是,识别的类别是同样的,但是可能上下文的处境是不一样的。
举个例子是 学习 同一个物体在不同照明条件下的识别,或者 学习在不同天气条件下驾驶汽车。
no data of previous tasks
这篇文章的设定还有一个点,那就是 no data of previous tasks can be store, 即在学习下一个任务的时候,不能得到之前的任务的数据。
事实上,对于解决 continual learning 的灾难性遗忘问题,有一个最粗暴的方法,那就是在进行第二个任务的训练学习过程中,保留之前所有任务的数据,来进行训练。 很明显,这种方法就会对训练和存储都带来很大压力。
但是,站在神经网络的角度,将之前所有任务的数据一起训练,这时候应该会得到最好的效果。所以这个设置一般在 continual learning 领域是所有方法的效果的上限,称之为 Joint Training 方法 .
保留之前任务的所有数据是显然不合适的。那么有的方法就退而求其次,保留之前任务的所有数据自然是不可行的,但依旧可以选择保留之前任务的小批次数据。对于保留下的一小批数据,最好这些数据是所有数据中的最有代表性的。 这就是 example-pir 的方法。
更进一步的设定,就是在训练新的任务的时候,只有上一个任务训练完的模型和新的数据,不能获得任何之前任务的数据,这便是本文的设定 no data of previous tasks 。
上面是对于是否能够获得之前任务的样本数据的设定。
但其实如果有一个存储的话,即使不能存储之前任务的原始数据,但依旧可以存储一些其他的和原始数据相关的内容。
比如存储原始数据的对应特征,或者训练一个生成网络,把能够生成之前任务的原始数据的模型给保存下来。
当然,还可以进一步限制这个设定,就直接没有一个存储器给你存储任何和之前数据的信息,只能提来你的模型去记忆。
embedding space
这一系列的文章的工作都是在 embedding space上做文章。
什么是 embedding space 呢? 在介绍之前先看一下神经网络的结构。
middle layer
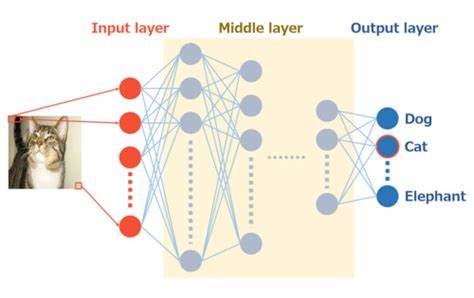
以图像识别为例,可以将网络按着顺序简单分为 Input layer ,Middle layer 和 Output layer.
Input layer 一般是网络的第一层,和输入的图像直接相关联,
Output layer 一般是网络的最后一层,最终直接和输出分类结果相关联。它也一般称之为clssifer ,就是认为后面的几层网络的作用就是来进行分类的。
那么中间的Middle layer的作用一般就是认为在提取图像特征,把输入图像在Middle layer 的最后一层的对应输出就可以认为是 这个图像的 embedding space.
|  |
但其实说,Middle layer 中间这一层可不可以认为也是 embeding space呢,当然可以,
因为从函数角度理解,每一层都是在对图像进行变换,每一次都会变换到新的空间中,哪一层都可以叫做embedding space了,也就是所谓的特征空间。
CNN
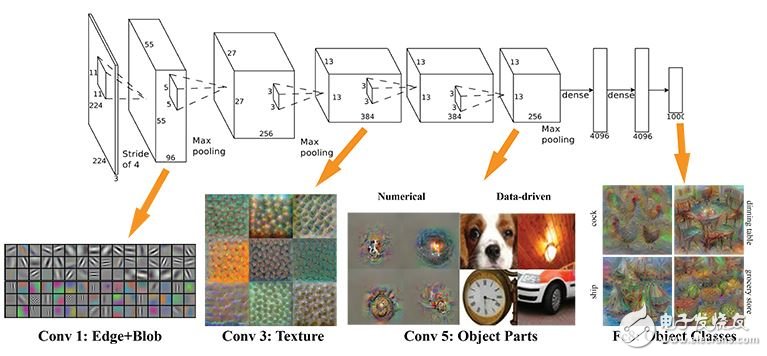
但还需注意,其实并不是middle layer的每一层都可以认为是 embedding space。在图像识别领域常用的网络比如CNN,一般来说,不同的层提取的特征是不一样的。如下图所示,在第一个卷积层,提取到的只是边缘信息,到了后面才是物体的整体特征比如狗的脸。一般认为处于后面的这个卷积层提取到的特征才称为 embedding space,即这一层的输出可以认为是很好地提取到了原始图片的特征,可以用来代表原始图片。
NLP
在NLP领域,同样也是有着 特征空间,embedding space的概念。
Static Word Embedding
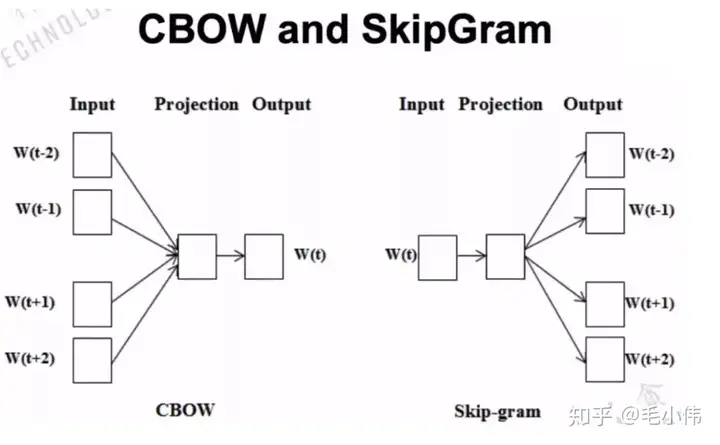
在论文 word2vec ,也就是 attention出现之前的时代,词向量就认为是文本的特征空间,其做法就是将文本进行编码,即通过神经网络将 文本映射到一个向量vecotr上,这就是embedding。
这种方法就类似于一个大词典,拿出来的词是一致的。
Contextualized(Dynamic) Word Embedding
上述的 还只是如何将单词进行编码,但是没有解决 一词多义的问题。即对于 苹果这个词向量,它是应该和 橘子 的距离更近呢,还是和 华为 的距离更近呢? 就是一个词语在不同的语境中是不同的含义。于是就有了 attention,也就是 transformer.
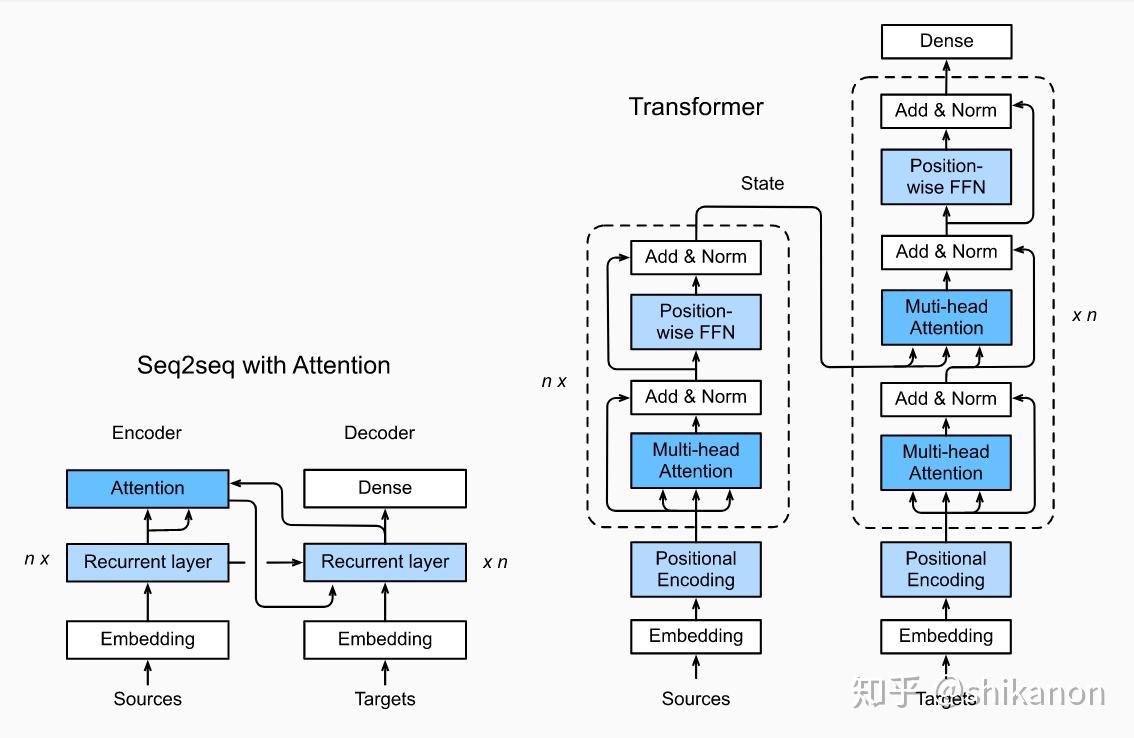
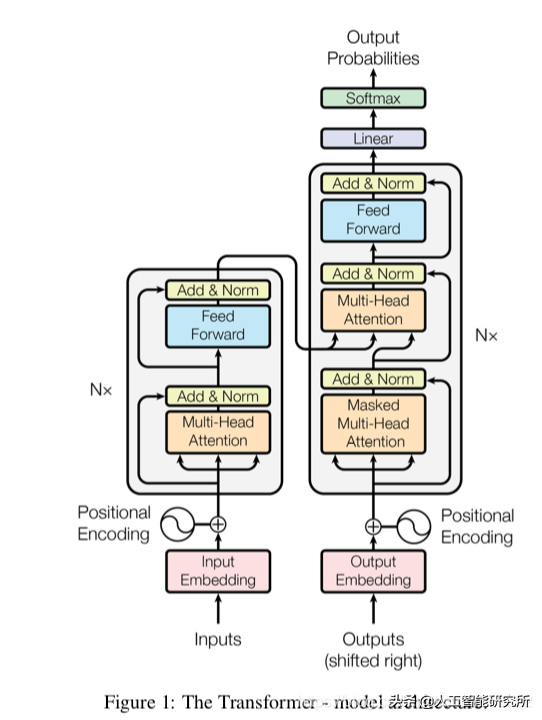
介绍一下 transformer的做法
首先直接使用一个巨大的字典作为 embedding ,将文本变成了数字编码,每个数字编码与一个词对应。
接着之后再加入位置信息,这个时候输入文本就变成了一个向量,这个向量不仅仅和这个词对应还加入了在文本中的位置信息。
然后再进行一系列的注意力机制来得到向量之间的关系,这时候就得到了文本中的单词的最终代表向量。
最后,再经过线性层与softmax 得到最终输出,这个就是上面所说的 clssifer,分类器,代表着最后一层。
下面是 attention 机制的网络架构与解释
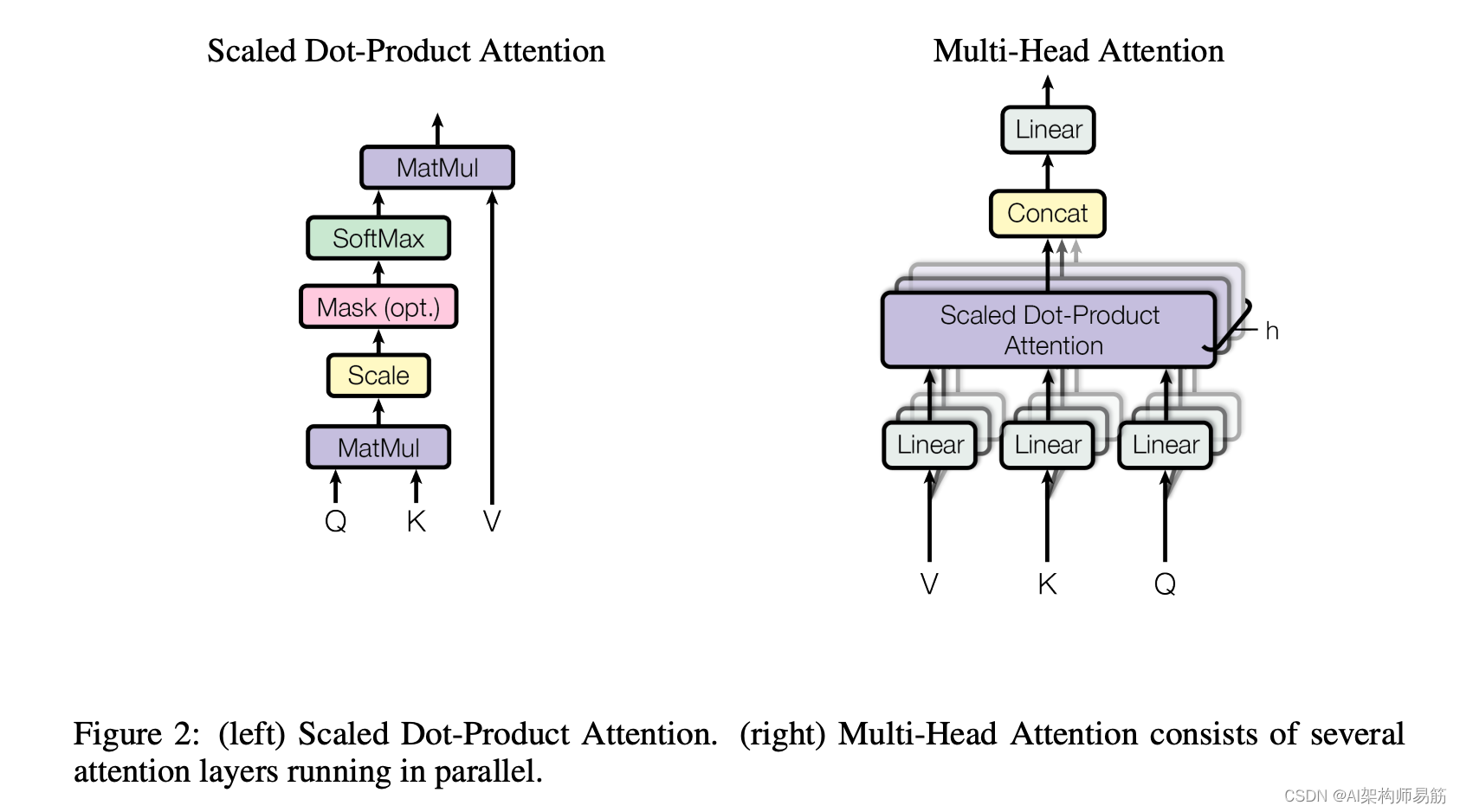
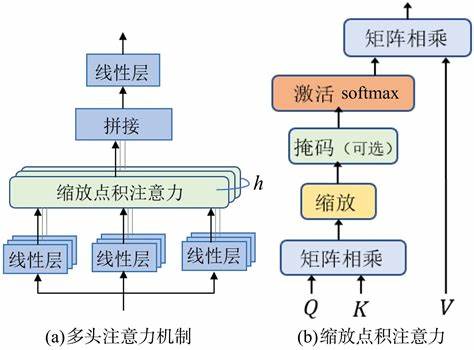
最终的输出结果之前的向量就可以认为是这句话的特征向量表示了。在 NLP的特征空间中,特征向量的距离一般使用 cos 函数来进行衡量。
那么我们想要的embedding space 是怎样的呢。即特征空间对特征向量的距离的度量能够和人类理解的含义是一致的。
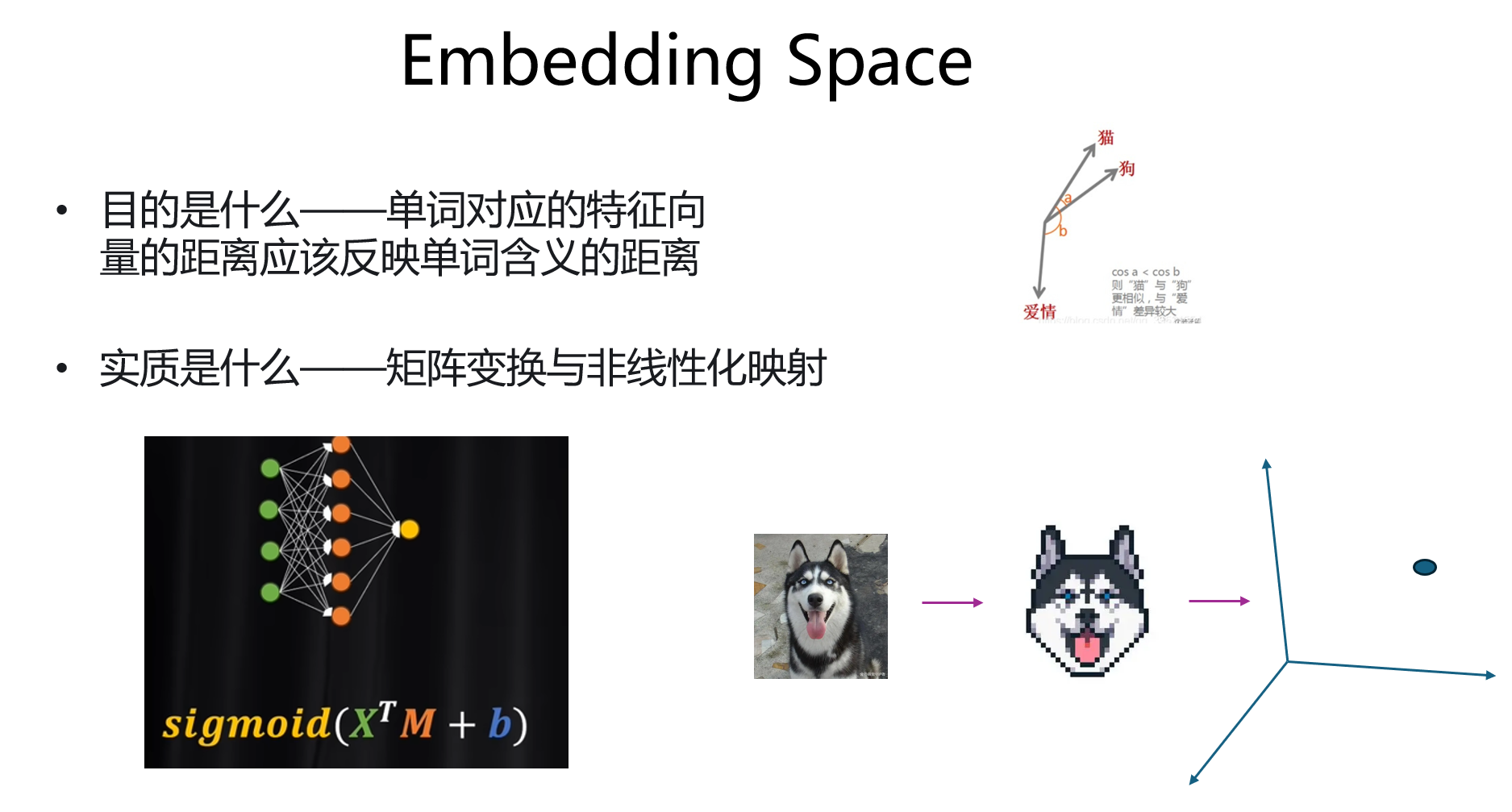
接下来,我们从第一篇工作开始看
NCM 分类器
NCM (Nearest Class Mean) 是一种简单但有效的分类方法,特别适用于embedding 网络的分类任务。NCM 分类器的核心思想是通过计算每个类的 所有样本的平均 embedding向量 (称为原型),然后将待分类样本与各类原型的距离进行比较,选择距离最近的类作为该样本的预测类别。
工作原理
类原型计算:对于每个类 $c$,首先计算其所有训练样本在 embedding 空间中对应的特征向量的 均值,称为类原型 ($\mu_c$)。公式如下: \(\mu_c = \frac{1}{n_c} \sum_{i} [y_i = c] z_i \tag{1}\)
其中 $n_c$ 是属于类 $c$ 的样本数,
$[y_i = c]$ 是指示函数,当样本 $i$ 属于类 $c$ 时取值为 1,否则为 0,
$z_i$ 是样本 $i$ 的embedding 向量。
最近类均值分类:对于每个测试样本 $z_j$,计算其embedding 向量与每个 类原型 之间的距离。通常采用欧几里得距离: \(c^*_j = \arg\min_{c \in C} \text{dist}(z_j, \mu_c) \tag{2}\) 其中 $\text{dist}(z_j, \mu_c)$ 通常是 $L2$ 距离(即欧几里得距离),$\mu_c$ 是类 $c$ 的原型。
$\arg\min$ 表示找到使得距离最小的类 $c$,并将该类作为样本 $z_j$ 的预测类别。
使用 NCM 进行分类的步骤
假设你目前有一些待分类样本,并且已经有了训练数据,可以按以下步骤使用 NCM 进行分类:
**数据embedding **:
- 训练一个embedding 网络,将所有训练数据映射到embedding 空间中。embedding 网络的目标是将相似的样本映射到彼此靠近的位置。
计算类原型:
对于每个类 $c$,计算所有训练样本的平均embedding ,得到每个类的原型 $\mu_c$。
类原型是这个类在embedding 空间中的“中心”。
分类待测样本:
- 将待分类的样本也通过同样的embedding 网络映射到embedding 空间。
- 计算每个待测样本与所有类原型的距离。
- 找到距离最近的类原型,并将该类的标签赋予该待测样本。
示例
假设你有三类数据 $A$、$B$ 和 $C$,每类有各自的训练样本。
- embedding 样本:
- 使用embedding 网络对每个样本进行embedding ,得到这些样本的embedding 向量。
- 计算原型:
- 类 $A$ 的原型:$\mu_A = \frac{1}{n_A} \sum_{i} z_i^{(A)}$,这里 $z_i^{(A)}$ 是类 $A$ 的embedding 向量。
- 类 $B$ 和 $C$ 同样计算各自的类原型。
- 分类新样本:
- 将新样本通过embedding 网络,得到embedding 向量 $z_j$。
- 计算该embedding 向量与类 $A$、$B$、$C$ 原型之间的距离。
- 选择距离最小的类作为新样本的分类结果。
NCM 的优点在于它在处理类增量学习(Class-Incremental Learning)时不需要为每个新类添加新的参数,只需要在原型集合中加入新类的均值原型。因此,它非常适合那些类不断增多且存储受限的情形,尤其在embedding 学习中,NCM 是一种计算简单、内存消耗小且性能可靠的分类方法。
SDC : Semantic Drift Compensation for Class-Incremental Learning
main idea
问题
通过上面的介绍就知道了文章要解决的问题,没有之前任务的数据,如何仅通过之前训练好的模型来解决灾难性遗忘问题。
目前可以利用的工具
- 之前任务训练好的模型
- 当前任务的数据
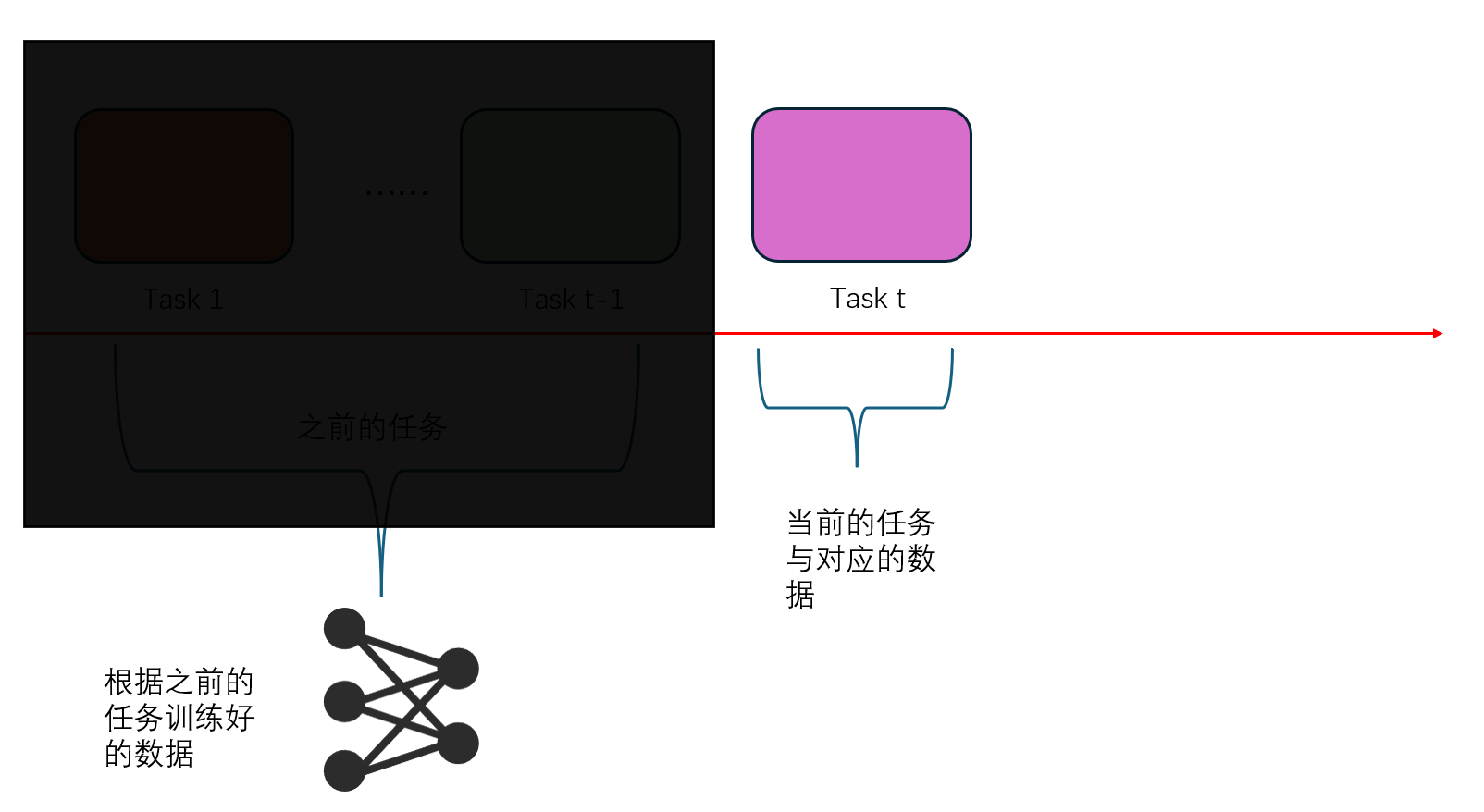
想法其实还蛮令人惊奇的,就是利用当前任务 $t$ 的样本 $D^t$在 模型 $M^{t-1}$ 和 $M^{t}$ 所生成的特征的对应关系。
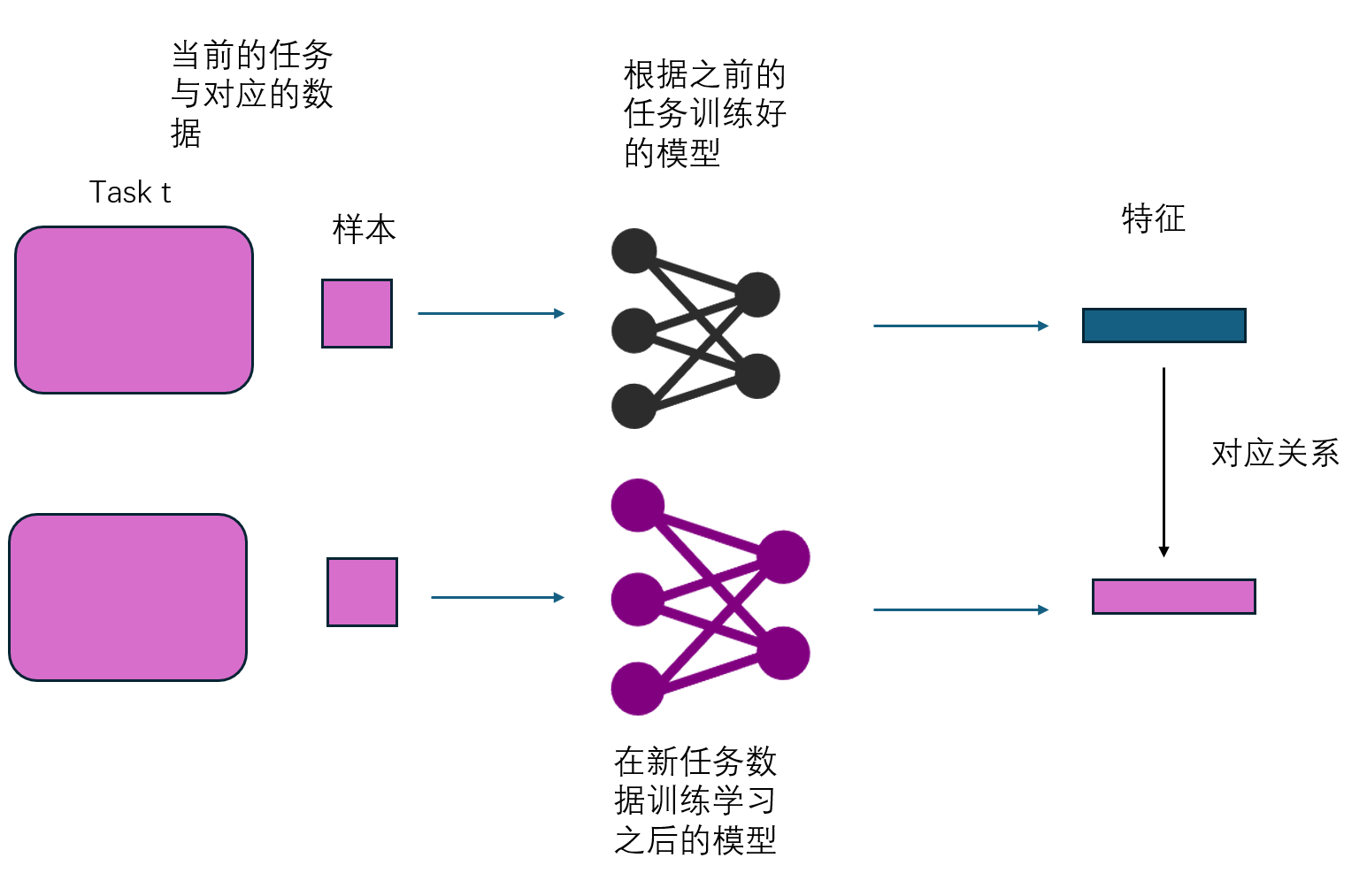
本篇论文设定为:
解决的问题为 Conitnual learning 中的 class-increntmental learning
提出的一个思路是
遗忘是由于类均值中心在新的embedding net的映射下出现了漂移 解决 semantic drift 问题
本篇论文使用的主要网络架构如下
- 使用 embedding network 作为特征提取器,将原始数据映射到 embedding space 。这里的embedidng network 就是指一个类似CNN的网络结构。
- 然后 使用NCM (nearest class mean)来作为分类器,其做法是将特征空间里的向量进行聚类,得到若干个特征向量簇的中心点,然后判断新的图像与每个中心点的距离来判断其应该所属于的类别。
在介绍本文工作之前需要介绍一些背景知识,首先是本文提出的一个概念 senmatic drift.
semantic drift
令continual learning 的流数据任务序列为${1,2,\dots,t-1,t,t+1,\dots}$,
当前任务为 $t$ ,之前的任务为 $t-1$ .
令模型用 $M$ 表示,则在进行任务 $t$ 的学习之前有根据之前任务训练得到的模型 $M^{t-1}$ , $M$ 是一个神经网络,可以将其分为两部分,分别是特征提取器 $MS$ 和 特征分类器 $MC$.
在文中,特征分类器就是NCM分类器也就是这里的$MC$, 它不需要学习且能够适应类别的增加。只要embeding network 足够好,那么应用NCM的计算公式就能进行分类区分。
而特征提取器就是文中的 embedding network, 即将样本映射到特征空间中。 模型的学习过程就是指这一部分的变化。
令数据集用 $D$ 表示,则在进行任务 $t$ 的学习之前有数据 $D^{t-1}$, 在进行任务 $t$ 时候,对应的训练数据为$D^t$。 数据集里的数据的形式为 图像-标签的数据对 $(x_i,y_i)$ ,这里$x_i$ 指的是图像,$y_i$ 指的是其类别。 第$t$ 个任务包含了 $C^t={c^t_1, c_2^t,\cdots,c^t_m}$ 种类别。
对于不同的任务 $t$ 和 $ s$ ,有着不同的类别,彼此没有重叠,即 $C^t \cap C^s =\empty $ 。在进行训练任务$t$ 时,其中的类别 $C^t$ 在之前所有的任务中都没有出现过。
接下来通过说明本文的主要思路
对于任务 $1$ , 在其数据 $D^1$ 训练得到一个 embedding network $MS^1$ , 此时有一个对应的 NCM 分类器。 此时数据有着 $C^1$ 个类别。对于这些类别,理论上每一个类别都有着一个“原型” propotype ,$\mu^{1}_{C^1_j}$ ,也就是类特征向量的均值。 此时NCM分类器能够将这些类别进行很好地区分。
接着,有了任务 $2$, 训练得到一个新的 embedding network。在continual learning 的设置中,进行第二个任务的训练的时候,只有第二个任务的数据 $D^2$ 。在这时,训练的目标只是要求 $M^1$ 在这些数据上表现得足够好。 此时 训练后的 $MS^2$ 和 NCM 分类器能够在任务二的数据上做得足够好,能够将任务二的数据都分得很清楚。
但这种训练不能保证 embeeding net 和 NCM 是否还能在原来的任务1做的足够好。
将原来任务 $1$ 的 某个样本 $(x_i^1,y^1_j),y_i =c^1_j \in C^1$ 的数据 $x^1_i$ 丢到 新的 embedding neteork $MS^2$ 中, 这时候会得到 一个特征向量 $z_i^2$ 。
然后由于我们记录了之前任务 $1$ 的所有 类原型 $\mu^{1}{C^1} = {\mu^{1}{c^11}, \mu^{1}{c^1_2}, \cdots}$ ,这时候 根据 公式 (2) 就能够将其分类到某个类别下。
但显然 $z_i^1 \neq z_i^2$, 这时候 对于样本$i$,其特征向量之差为 $\delta^{t-1 \rightarrow t}_i = z^{t}_i - z^{t-1}_i$ 。
同样的 原来的 类原型也会随之发生变化 $ (\mu^{1}{c^1_j}) \rightarrow (\mu^{2}{c^1j}) $,这就导致按着之前计算得到的类原型 $\mu^{1}{c^1_j}$ 进行分类,可能会出现分类错误的现象。
\[\begin{aligned} x_i^1 &\xrightarrow[]{MS^1} z^1_i (\rightarrow \mu^{1}_{c^1_j}) \\ x_i^1 &\xrightarrow[]{MS^2} z^2_i (\rightarrow \mu^{2}_{c^1_j} \neq \mu^{1}_{c^1_j}) \end{aligned}\]我们知道之前 所有地类原型$\mu^{1}_{C^1}$的信息,但 这些类原型在新的embedding network 下可能不再适用。NCM 分类器只是根据类原型按着距离来进行分类,对于这种效果下降,NCM表示它不背锅。
作者认为这是因为 任务 $1$ 中的 类原型 $\mu^{1}_{c^1}$ 发生了位置漂移 semantic drift 公式如下。 直观理解就是,特征空间中,类的中心点的位置发生了移动,导致NCM分类器按着距离无法进行区分。
\[\Delta^{1 \rightarrow 2}_{c^1_j} = (\mu^{2}_{c^1_j}) - (\mu^{1}_{c^1_j})\]对于任务 $1$ 中地所有类$c_j^1 \in C^1$, 都有着它们自己的一个类原型地漂移,将其联合起来,就得到了整个任务地所有类地 漂移之和
\[\Delta^{1\rightarrow 2}_{C^1} = \sum_{c_i^1 \in C^1} \Delta^{1 \rightarrow 2}_{c^1_j}\]如果能够得到这个位置漂移的量,对于之前类别的数据应用这些补偿,即在之前记录下的类均值加上位置漂移,作为分类的依据,而不是直接使用之前记录的类均值,这样做应该能够得到更好的分类效果。
\[x_i^1 \xrightarrow[]{MS^2} z^2_i \quad ( \mu^{2}_{c^1_j}=(\mu^{1}_{c^1_j}+ \Delta^{1 \rightarrow 2}_{c^1_j}))\]那么 NCM分类器 任务 $1$ 的类别上依旧能够表现地很好。使用这种方法来解决 灾难性遗忘的问题。
?疑问1
但其实这有一个问题呀,那就是这两个特征向量分别是怎么获得的,按着我的理解,这都不是同一个模型了,咋还能计算特征向量的关系?
仅仅是因为层数相同,所以对应的特征向量的维度相同吗,就把这个来作为drift,搞不懂,得看一下代码
这个想法很直接,但其背后有着较强的假设
1 新的网络和旧的网络 ,输入同一个数据,得到的应该并不是同一个特征空间,毕竟网络的架构都变了,其函数的映射方式已经发生变化了。但作者直接忽略了这个事实。认为两者都映射到了同一个空间, 其变化只是简单的位置差异。
作者这么处理有着很方便的地方就是 这两个特征向量的维度是一致的,所以是能够进行上述的直接加减的操作,但也有可能虽然维度一致,但每个维度代表的含义就根本不一样。
how to solve sematic drift
按着这种想法,分类效果下降只是因为位置发生了 漂移 ,那么只需要对这些之前的类别的漂移加以弥补,那么NCM自然还能够很好地工作。
但是为什么要计算漂移量呢,费这么大劲干嘛?
最简单的是直接把所有数据拿过来,重新训练得到一个 embedding model ,将数据映射到 所有的类别 通过NCM都能很好分开的 特征空间上不久好了吗?但别忘了,文章的设定实在continual learning 上进行了,所以不能很多之前的数据来进行训练。
奥,这个计算其实很简单,只需要有任务 $1$ 的某些数据,然后统计一下 这些的特征的移动的平均值来即可 ,如下:
\[\begin{aligned} \Delta^{1 \rightarrow 2}_{c^1_j} & = (\mu^{2}_{c^1_j}) - (\mu^{1}_{c^1_j}) \\ & = (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^2_i) - (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^1_i) \\ & = \frac{1}{n_c} \sum_{i} [y_i = c^1_j] (z^2_i - z^1_i) \\ & = \frac{1}{n_c} \sum_{i} [y_i = c^1_j] (MS^2(x_i^1) - MS^1(x_i^1)) \\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i = c^1_j] (MS^2(x_i^1) - MS^1(x_i^1))}{\sum_{i}^{N_{sample}} [y_i = c^1_j]} \end{aligned}\]所以如果有 任务一的某些 ($N_{sample}$)个样本 $x^1_i$ ,
在任务 $2$ 训练之前的模型 $MS^1$ ,就能得到 上式中的 $MS^1(x_i^1)$
然后将其放到 任务$2$ 训练之后的模型 $MS^2$, 就能得到 $MS^2(x_i^1)$
使用这两者的差值就能用来 估计 其所属于的类的均值中心的漂移了
为什么这里说是估计而不是计算呢,这是因为我们利用的是若干个之前任务的样本来估计真正的类均值,而如果是计算的话,那就应该是使用训练任务 $1$ 的所有数据来计算
但别忘记了,本篇论文时设置无法获得之前任务的样本 ,所以上述方法就是不可行的了。
那么怎么解决呢? 别急,我们没有之前任务 $1$ 的样本 $x^1_i$ , 但我们有当前任务 $2$ 的样本 $x^2_i$ ,
只需要先将 $x^2_i$ 放到 模型 $MS^1$ 中,就能得到 其对应的特征 $z_i^1$,然后在模型训练后将其丢到模型 $MS^2$中, 就能得到其对应的特征 $z_i^1$ ,那么这两个特征向量的差值 也可以用来估计 其所属于的类的均值中心的漂移了 。如下所示:
\[\begin{aligned} & MS^2(x_i^2) - MS^1(x_i^2) \\ &= z^2_i - z^1_i \\ &= \delta^{1 \rightarrow 2}_i \end{aligned}\]得到上述之后特征向量的差值, 就能按着上述式子来进行来估计 ,
\[\frac{\sum_{i} [y_i = c^1_j] \sigma_i^{t-1 \rightarrow t}} {\sum_{i} [y_i = c^1_j]}\]但是有一个问题,在新的任务下,新的样本 $x^2_i$ 的类别只可能属于新的类别 $ C^2$ ,其不能很好地估计出之前任务的某一个类别 $c^1_j \in C^1$ 的漂移。
作者直接采用了不同任务之间的漂移,即使用 当前任务的所有类别的漂移之和 来 估计之前任务的某个类别的漂移之和 。
如下所示
\[\begin{aligned} \Delta^{1 \rightarrow 2}_{c^1_j} \\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i = c^1_j] (MS^2(x_i^1) - MS^1(x_i^1))}{\sum_{i}^{N_{sample}} [y_i = c^1_j]} \\ &\text{Using }x_i^2 \in D^2 , \ \text{ranther than } x_i^1 \in D^1\\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i = c^1_j] (MS^2(x_i^2) - MS^1(x_i^2))} {\sum_{i}^{N_{sample}} [y_i = c^1_j]} \\ &\text{But No such point } y(x_i^2) = c^1_j \in C^1 , \ \text{Only point } y(x_i^2) = c^2_j \in C^2\\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i = c^2_j] (MS^2(x_i^2) - MS^1(x_i^2))} {\sum_{i}^{N_{sample}} [y_i = c^2_j]} \\ &\text{Just average for all } c^2_j \in C^2 \\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i \in C^2] (MS^2(x_i^2) - MS^1(x_i^2))} {\sum_{i}^{N_{sample}} [y_i \in C^2]} \\ &\text{But average means nothing, want some represent point} \\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i \in C^2] (MS^2(x_i^2) - MS^1(x_i^2)) \cdot w_i} {\sum_{i}^{N_{sample}} [y_i \in C^2] \cdot w_i} \\ & \text{point} \ y(x^2_i) \sim c^1_j \in C^1 \text{is more important} \\ &w_i = \exp{ -\frac{ ||MS^1(x_i^2)-\mu_{c^s_j}^{1}||}{2 \sigma^2}} \end{aligned}\]上面式子就只利用到了 第二个任务的样本 $x_i^2$ ,训练之前的模型$MS^1$和训练之后的模型 $MS^2$ ,用来估计得到了 模型漂移 $\Delta^{1 \rightarrow 2}{c^1_j} $ 。 这时候再加上之前记录下来的类原型 $\mu^{1}{c^1_j}$ 就能直接来对之前的任务进行分类了。 但只用了第二类不同类别的位置差异的平均值,可能不具有什么代表性。我们更想要的是哪些与
这篇工作的和上式结果还有一些差别,差别在于添加了一个权重项$w_i$ ,在本篇文章中的公式如下
\[\hat{\Delta} ^{t-1 \rightarrow t}_{c^s_j} = \frac{\sum_{i} [y_i \in C^t] \sigma_i^{t-1 \rightarrow t }w_i} {\sum_{i} [y_i \in C^t]w_i}\]其中,
$\hat{\Delta}^{t-1→t}_{c_s}$ 表示从任务 $t−1$ 到任务 $t$ 的类 $C^t$ 的语义漂移估计,
$\delta^{t-1→t}_i$ 是从任务$t-1 $ 到任务 $t$ 的数据点 $i$ 的漂移向量,
$[y_i \in C_t]$ 是指示函数,当样本 $i$ 属于类 $C_t$ 时取值为 1,否则为 0,
而 $w_i$ 是一个权重因子,用来衡量数据点 $i$ 与要估计的类原型之间的相似度。
\[w_i =e^{-\frac{ ||z_i^{t-1}-\mu_{c^s_j}^{t-1}||}{2 \sigma^2}}\]这个公式用于计算每个点 的权重 $w_i$,它是一个高斯核函数。
权重 $w_i$由数据点的 embedding 向量 $z^{t-1}i$ 与类原型 $\mu{c^s}^{t-1} $ 之间的距离决定。这个类原型就是要被估计的类的 向量均值。 这里的 $z^{t-1}_i = MS^1(x_i^2)$
样本距离要估计的类原型 距离越小,数据点对类原型漂移估计的贡献越大。
参数 $sigma$ 控制高斯核的宽度,即控制相似性衰减的速度。 上式说明距离样本均值 在标准差范围之内的样本有更大的权重。
为什么要设置这个权重呢?
因为上面提到 作者是 用 当前任务的所有类别的漂移之和 来 估计之前任务的某个类别的漂移之和 。这样的估计很粗略,甚至不一定有效 。
作者想要的是 使用新数据 估计 旧类的类原型的移动。 这就遇到了我们之前提到的问题,新数据应该不属于旧的类,那么就只能依靠哪些离旧的类比较接近的数据去估计。这也就是这个 权重的作用。使得哪些靠想要估计类距离较近的数据发挥作用。
思考
但总感觉文章绕了一个好大的圈子。而且直接使用距离来计算未免显得过于粗暴,毕竟这是不同的模型,是存在一个映射然后在同一空间然后进行计算的。
ADC : Resurrecting Old Classes with New Data for Exemplar-Free Continual Learning CVPR2024
我们来继续介绍下一篇,上一篇的核心思想就是
- 直接使用距离来描述 样本向量 在新旧的样本空间下的变化。
- 在不能得到之前任务的样本下,使用新数据 估计 旧类的类原型的移动 。
- 使用高斯核函数来选择那些距离 旧类原型 尽可能近的新样本 来估计 旧类原型的移动 。
这种选择是否是一个足够好的选择呢?
按着SDC的方法,不管怎么选择,还是从新任务的数据中选择一个尽可能好的样本来进行估计。
但如果两个任务相差很大,那么第二个任务的数据可能就跟不找不到 使得权重 $w$ 很大的显著样本。那么就成了退化成了就差的情况,即使用第二个任务的 整体样本的便宜来估计第一个任务中的某一类数据的漂移。 这很可能是没办法用的。
因此,ADC就提出来解决这个问题。既然现成的数据没法用,那么我们干脆自己来 生成一些 距离旧类原型 尽可能近的样本 来估计 旧类的类原型的移动。
对抗样本的生成
如何生成一些 比第二个任务地样本 更靠近某一类地样本呢?
分两步,
第一步,和SDC 所使用的高斯核函数一样的思路。首先在新任务地数据中,找到一些距离 旧类原型 比较近的样本。
第二步,将这些样本朝着旧类原型进行移动。
我们接下来详细看一下如何完成这两步吧。 这里我们依旧采用上面的符号,并使用任务1和任务2作为例子来进行表述。
任务 $1$ 训练完成后得到 一个 其所有的类的原型 ,对于其中某一个类$k \in C^1$ ,其对应有一个类原型 $\mu^1_{k}$ 。 此时对应的embedding network 为 $MS^1$
任务 $2$ 的数据集为 $D^2$ , 从中采样得到 $m$ 个和 第 $k$ 个类别的旧类原型 $\mu^1_{k}$ 较近的样本 $X^2_k$ 。
接下来,我们要根据这些个样本集合 将其进行移动,来获得一些更好的样本集合 即对抗样本集合 $X^{adv}_k$。
这个对抗样本集合的元素 $x^{adv}_k$ 由于足够接近 旧类原型 $\mu^1_k$ ,因此在旧模型下,会被NCM 分类器 分类为 $k$ 类别。
\[k = \arg\min_{y \in C^{1:t-1}} \Vert MS^1(x_k^{adc}) - \mu^1_k \Vert_2\]然后根据 对抗样本集合 与 旧类原型的L2 平均距离最小 设为 优化目标函数 ,即
\[L(MS^1,\mu^{1}_{k},X^2_k) = \frac {\sum_{x \in X^2_k } \Vert MS^1(x) - \mu^1_k \Vert_2 } {|X^2_k|}\]然后为了将这些样本朝着旧类原型移动,对优化目标进行求导来得到梯度, 即
\[\nabla_x L(MS^1,\mu^{1}_{k},X^2_k)\]然后 将其除以模长 就得到 单位梯度方向,再乘以步长$\alpha$, 就得到了梯度更新方式如下:
\[x^{adv}_k \leftarrow x - \alpha \frac{\nabla_x L(MS^1,\mu^{1}_{k},x)}{\Vert \nabla_x L(MS^1,\mu^{1}_{k},x) \Vert_2} \quad \forall x\in X^2_k\]这就是针对对 第一个任务中的类别 $k$ , 使用第二个任务的数据 $X^2k$ ,来获得 对类原型 $\mu^1_k$ 的 对抗样本 $x{adv}$的步骤。 更一般的,将上面式子中的 $1$ 替换为 $t-1$ ,就得到了论文中的式子
\[x^{adv} \leftarrow x - \alpha \frac{\nabla_x L(MS^{t-1},\mu^{t-1}_{k},x)}{\Vert \nabla_x L(MS^{t-1},\mu^{t-1}_{k},x) \Vert_2} \quad \forall x\in X^2_k\]根据上述设置,我们就得到了一些 更好的对抗样本集合 ${x_{adv}}$
漂移的估计
然后类似SDC的设置,接下来就是使用这些对抗样本的漂移来评估 任务$t-1$ 的 $k$ 类 的类原型 在新旧类之间的漂移
\[\Delta ^{t-1 \rightarrow t}_k = \frac{\sum_{x_{adv} \in X^{adv}_K} MS^{t}(x^{adv})-MS^{t-1}(x^{adv}) }{|X^{adv}_k|}\]然后对应新的特征空间下的类样本原型为
\[\mu^t_k = \mu^{t-1}_k + \Delta ^{t-1 \rightarrow t}_k\]思考
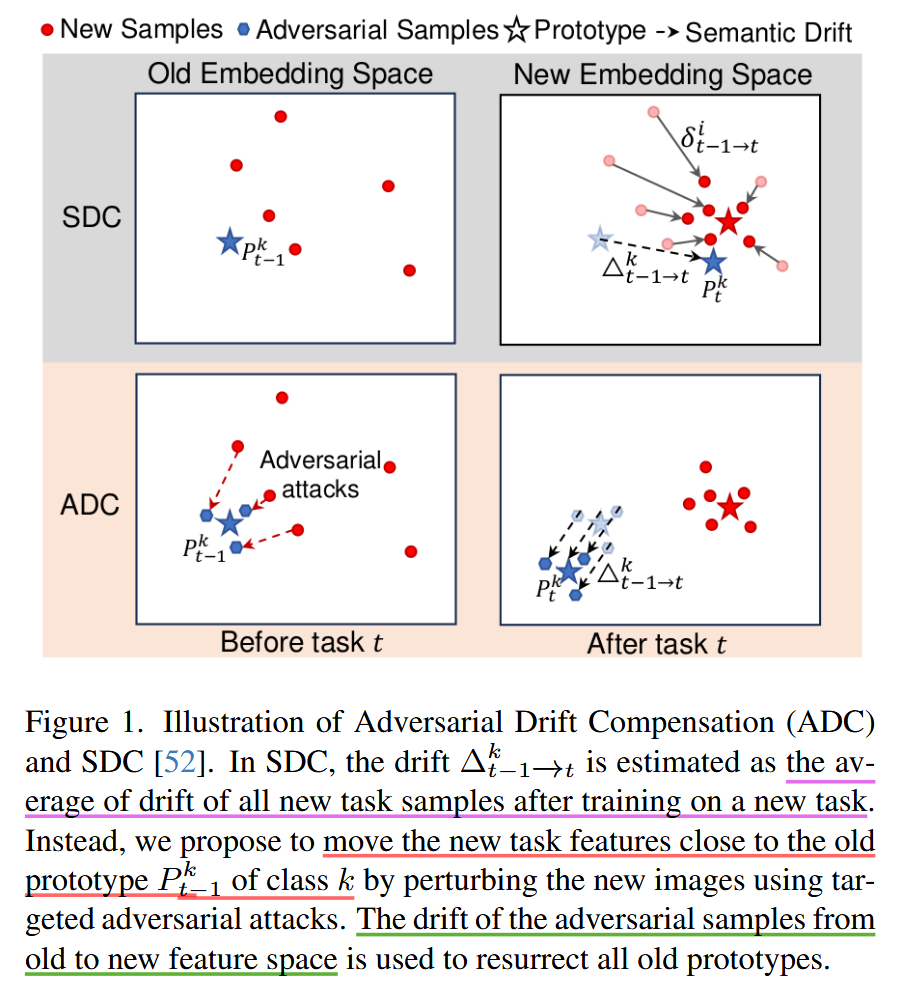
根据第一篇文章总结的点来看,ADC的思路依旧遵循了第二步,然后改进了第三步,选择并改进生成了一些距离 旧类原型更近的样本。
LDC : Exemplar-free Continual Representation Learning via Learnable Drift Compensation ECCV2024
总结一下上面两篇论文的核心思想
SDC:
- 直接使用距离来描述 样本向量 在新旧的样本空间下的变化。
- 在不能得到之前任务的样本下,使用新数据 估计 旧类的类原型的移动 。
- 使用高斯核函数来选择那些距离 旧类原型 尽可能近的新样本 来估计 旧类原型的移动 。
ADC
- 直接使用距离来描述 样本向量 在新旧的样本空间下的变化。
- 在不能得到之前任务的样本下,使用新数据 估计 旧类的类原型的移动 。
- 在筛选出距离旧类原型较近的样本的基础上,进一步调整,得到 属于旧类的对抗样本 用来估旧类原型的移动
但ADC依旧没有解决我的疑惑,即第一步设置,直接使用距离来描述模型改进前后的变化是否合理呢?
仔细想一想其实不太合理,按着之前的符号表示,我们有
\[\begin{aligned} x_i^1 &\xrightarrow[]{MS^1} z^1_i (\rightarrow \mu^{1}_{c^1_j}) \\ MS^1 &\xrightarrow[]{D^1} MS^2 \\ x_i^1 &\xrightarrow[]{MS^2} z^2_i (\rightarrow \mu^{2}_{c^1_j} \neq \mu^{1}_{c^1_j}) \end{aligned}\]所谓旧类原型的漂移,实际上是因为 原来的 embedding model 发生了变化,之前的直接使用距离是一种很粗糙的做法,实际上两者相差了一个变换。 将第二个过程可以改写为下式
\[MS^2 = F(MS^1)\]则有
\[\begin{aligned} \Delta^{1 \rightarrow 2}_{c^1_j} & = (\mu^{2}_{c^1_j}) - (\mu^{1}_{c^1_j}) \\ & = (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^2_i) - (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^1_i) \\ & = \frac{1}{n_c} \sum_{i} [y_i = c^1_j] (z^2_i - z^1_i) \\ & = \frac{1}{n_c} \sum_{i} [y_i = c^1_j] (MS^2(x_i^1) - MS^1(x_i^1)) \\ & = \frac{1}{n_c} \sum_{i} [y_i = c^1_j] F(MS^1(x_i^1)) - MS^1(x_i^1) \\ &\sim \frac{\sum_{i}^{N_{sample}} [y_i = c^1_j] (MS^2(x_i^1) - MS^1(x_i^1))}{\sum_{i}^{N_{sample}} [y_i = c^1_j]} \end{aligned}\]可以看到 SDC, ADC 都是直接把两个模型之间的变换给忽略了 ,因此是存在很大的问题的。
所以,SDC,ADC直接用了两个向量的差值,但如果仅仅只是将原图像进行一个旋转变化,可能这样的对应关系就不存在了。而这其实是不合理的。
因此,即使是要估计这个漂移的差值,也应当得到这个 变换的,然后才能真正地进行估计。
怎么来做呢?
首先,如果能够获得 或者说 保存下来 任务 $1$ 的数据,那么做法其实也很简单,直接把这个数据放到前面的公式中,就自然能够得到这个样本真正的差值。
但很遗憾这个设定并不满足。那么可以尝试退一步,我们可以保存一些样本的代表数据,来进行上述操作。那这样其实也是可以的。
如果上述条件仍然不满足,就是不能保留任务$1$的数据,那怎么办?
不让我保存原始数据,那保存这个数据的特征可以了吧。
按着这个设定,即允许有一个内存,又不能保存原始数据,但我们可以将样本的特征给保存下来。
| 在完成训练任务 $1$ 之后,我们得到了模型$M^1$, 这包括特征提取器 $MS^1$ 和 $MC^1$。此外,我们还能够获得任务 $1$ 的一些样本的特征数据集合 $Z^1={z | z= MS^1(x^1),x^1 \in D^1}$,将这些数据保存在内存中。 |
| 然后继续进行任务 $2$ , 完成训练之后,能够获得 到了模型$M^2$, 这包括特征提取器 $MS^2$ 和 $MC^2$。此外,我们还能够获得任务 $1$ 的一些样本的在模型$MS^2$下的特征数据集合 $Z^2={z | z= MS^2(x^1),x^1\in D^2}$, |
这个时候两组特征向量依旧是无法进行比较,因此我们需要得到一个映射 将特征空间 $Z^1$ 转换到 特征空间 $Z^2$ ,我们将其称之为 特征空间变化网络 ,
\[f^{t-1 \rightarrow t} : Z^1 \rightarrow Z^2\]怎么得到这个变换呢,只需要我们得到相应数据即可。
我们只需要 来自任务 $1$ 的样本 $x^{1}_{i}$ ,其在第一个任务训练得到的特征提取器 $MS^1$ 下的 特征 $z^1_i$ ,然后这同一个样本 ,其在第一个任务训练得到的特征提取器 $MS^1$ 下的 特征 $z^2_i$ ,这样的话就能够训练一个神经网络来表示这个映射。
为了训练神经网络,我们需要定义一个损失函数
\[\begin{aligned} L(z^{t-1},z^t) &=L_{sim}(z^{t-1},f(z^{t-1})) \\ &= 1- cos(z^{t-1},f(z^{t-1})) \\ \end{aligned}\]为什么要使用 cos 来衡量 两个向量的差异呢,这是因为在NLP领域的 embeding space ,就是使用 cos 函数来衡量两个特征空间中的向量的差异。
两个向量的 cos 距离越近,其含义约相近,其值约接近1。
而我们是想要通过最小化损失函数来优化函数$f$ ,因此这边设定就是 $1-cos $ ,整体值越小,两个向量的 含义越接近。
余弦相似度的公式如下
\[cos(a,b) = \frac{a b}{\Vert a \Vert \Vert b \Vert}\]余弦相似度关注的是两个向量的方向,而非其大小。这在 Feature Distillation 中非常重要,因为深度学习模型的中间层特征往往是高维向量,且这些向量的大小(模长)可能会因不同数据样本或训练阶段产生较大变化。如果仅使用欧氏距离来衡量特征向量的差异,特征向量的大小可能会极大地影响损失函数,而这并不是模型训练的重点。通过使用余弦相似度,特征向量的模长被归一化为单位向量,因此不会因为特征大小的变化而影响学习效果,这使得损失函数更加专注于学习正确的特征模式或方向。
上面这些内容就是 另一篇论文
MEA Memory-Efficient Incremental Learning Through Feature Adaptation 的内容,这篇文章采用continual learngin的设定,不能得到之前任务的数据,但是却存储了之前任务数据的特征。
另外,这篇文章并没有和前面的SDC以及ADC 有了一个特殊的NCM来作为分类器,而是有着一个分类函数 $MC$ 。
所以 对于上述 特征空间变化网络,其不单单要保证 数据$x_i^1$ 的两个特征$z^1_i$和 $z^2_i$是一致的,还要保证之后的分类器$MC^2$也能将其正确分类。于是还定义了另一个损失函数如下
\[L_{cls}(MS^2, z^2_i,y) = \text{crossEntropy}(MS^2(z^2_i),y)\]就是一个交叉熵损失函数,这里的 $y$就是数据$x_i^1$的类别标签。自然这个属性也应该保存下来才能在后面进行使用。
综合上述两个其实就是 经典的Feature Distillation的损失函数定义 。
Feature Distillation 的目标是让学生模型不仅在输出结果上模仿教师模型,还能在特征空间中尽可能接近教师模型的中间层表示。其一般包括在 Feature Distillation 中,完整的损失函数通常是任务损失和特征蒸馏损失的加权和:
\[L = L_{\text{task}} + \lambda L_{\text{fd}}\]其中:
- $L_{\text{task}}$ 是标准的任务损失 Task Loss,如分类任务中的交叉熵损失。
- $L_{\text{fd}}$ 是特征蒸馏损失 Feature Distillation Loss,用于约束学生模型的中间特征向量与教师模型保持一致。
- $\lambda$是一个超参数,用于控制任务损失与特征蒸馏损失之间的权重平衡。
特征蒸馏损失用于让学生模型学习教师模型的中间特征表示。为了实现这一目标,学生模型的特征向量(通常来自隐藏层)需要与教师模型的特征向量保持相似。常见的除了上述的 cos函数定义还有其他定义,如L2 距离损失函数 ,Smooth L1 损失函数。
MAE这篇论文的设定
- 网络就是一般的网络架构,可以分为特征提取器和分类器
- 使用存储结构,用来存储之前任务数据的特征
- 训练一个 前后任务之间的 特征映射 ,损失函数是特征蒸馏函数
可以看到 MAE 和之前的SDC,ADC, 设定有很大差异,一个在于其使用了存储结构来保存特征,另外一个是基于一般的网络架构进行考虑,
如果我们继续之前 SDC,ADC的思路,抛弃掉MAE的第二个设定,限制在没有存储器的情形下,那么应该怎么做呢
首先,SDC,ADC 的核心思想是一致的,那就是找到 旧类原型在新的特征空间下对应的位置, 但是简单地使用了 距离 忽略了 不同空间地转换。
找到到 旧类原型在新的特征空间下对应的位置,这种做法真的有效吗
但首先问题是, 这个想法,即找到到 旧类原型在新的特征空间下对应的位置,这种做法真的有效吗?应当进行实验来检验验证这个想法。
LDC论文首先对这一点进行了验证,我们还是基于上述地任务一和任务二来讨论,
在完成训练任务 $1$ 之后,我们得到了模型$M^1$, 这包括特征提取器 $MS^1$ 和 $MC^1$ 。此时对于数据$D^1$ 的某一类 $c^1j \in C^1$数据,其类原型为 $\mu^1{c^1_j}$ ,类原型的计算是根据 $D^1$的训练数据得到的 ,即
\[\mu^1_{c^1_j} = \frac{ \sum_{i\in D^1} [y_i = c^1_j] z^1_i}{\sum_{i\in D^1} [y_i = c^1_j]}\]然后继续进行任务 $2$ , 完成训练之后,能够获得 到了模型$M^2$, 这包括特征提取器 $MS^2$ 和 $MC^2$。此时,对于第一个任务的 同一类的类原型,应当根据之前的训练数据 在新的特征提取器下来计算得到 ,即
\[\mu^2_{c^2_j} = \frac{ \sum_{i\in D^1} [y_i = c^1_j] z^2_i}{\sum_{i\in D^1} [y_i = c^1_j]}\]作者将第一个类原型 称之为 Naive prototypes , 第二个是 Oracle propotypes 。
此外,作者将第一类任务和第二类任务一起训练,这就得到了 Jonit trained 。
另外作者还使用 LDC方法 在第一个类原型的基础上进行了漂移的矫正,称为 Corrected prototypes。
在这些个不同的 类原型的基础上 使用NCM 分类器 对一些测试样本进行了分类,来测试这四个类原型的效果。结果如下表所示。
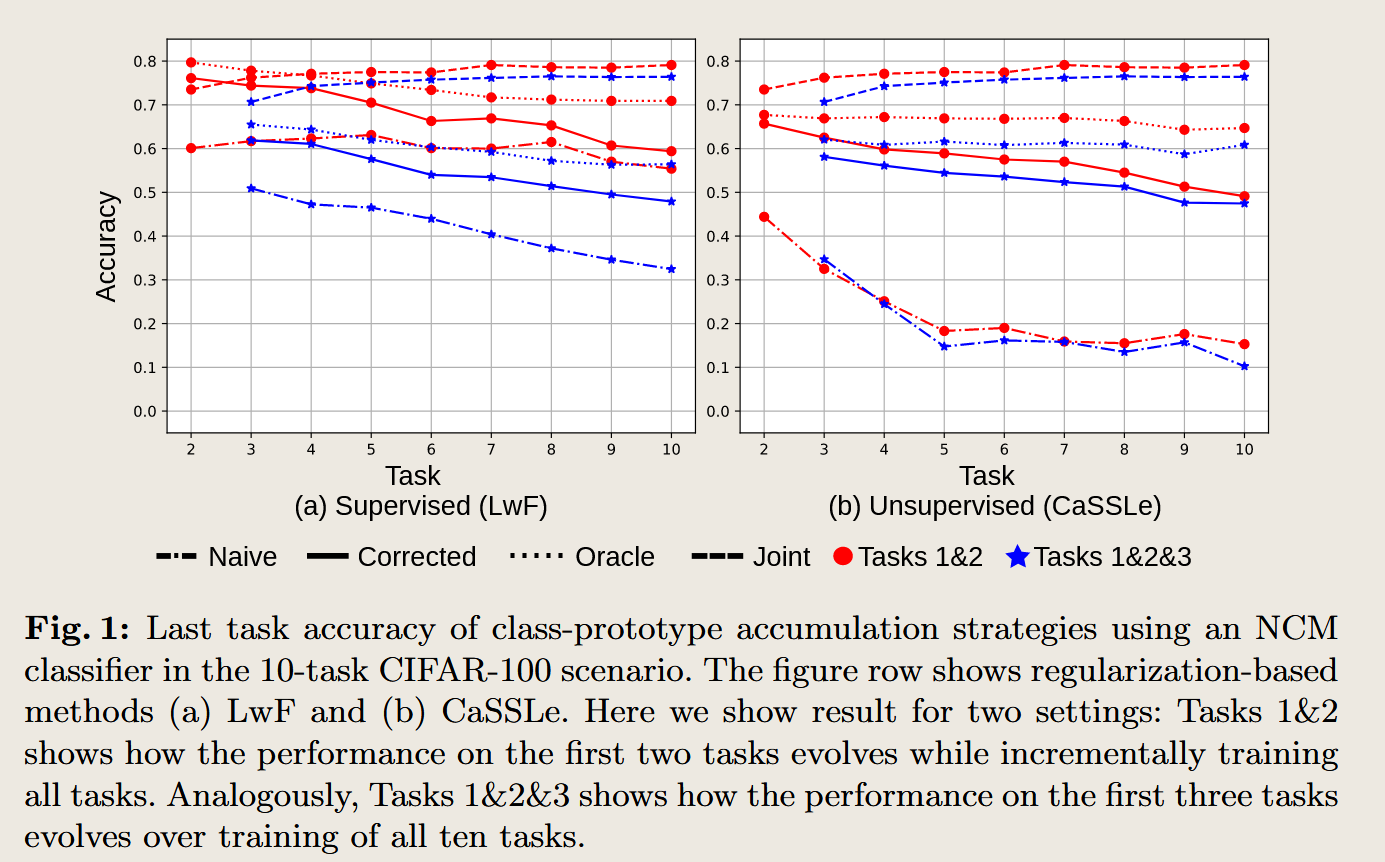
图 1 包含两个子图,分别对应于监督学习(LwF) 和 自监督学习(CaSSLe) 这两种持续学习策略下的实验结果。
作者使用了ResNet-18 网络作为特征提取器,并在 CIFAR-100 数据集上进行了 10 个任务的持续学习,每个任务包含新的类。
实验结果指标 为根据不同的类原型 使用最近类均值(Nearest Class Mean, NCM)分类器来对最后一个任务的分类准确度。以Naive prototypes为例,展示的是根据任务一训练得到的Naive prototypes,通过 最近类均值(Nearest Class Mean, NCM)分类器 在第二个任务上的效果。
四种原型策略分别如上所示。
结果显示 Naive Prototypes (p_naive) 和 Jointly Trained Prototypes (p_joint) 的性能存在较大差距,这种差距通常被称为灾难性遗忘。随着任务的增加,性能差距进一步扩大,说明传统的未经补偿的类原型逐渐失效。
这说明随着任务训练的不断进行,原先的类原型在新的映射下其不再是类样本特征值的中心。这有两个可能,一个是类原型跑偏了,另一个是类样本特征向量跑偏了,但更实际的情况是 两者都跑偏了,所以真正的类原型定义得到值也跑偏了。
还有一种情况是在新的空间中,原有的距离的度量的定义失效,导致类原型计算出错。
此时,如果我们根据类原型的定义,计算得到真正的类原型,称作 Oracle propotypes ,这时候应当能够得到一个较好的分类结果,实验也说明了这一点。这说明类原型的思想随着任务改变但依旧还起作用。
问题,为什么类原型依旧起作用,但是却没有 upper bound 方法来的好呢?
即使找到了所有训练样本理论上对应的类原型,但其分类效果依旧不如 upper bound, 这和分类方法的定义,度量的定义是不是有关系呢。
说随着样本增加,有一些样本依旧能够被 upper bound 分开,但却不能被 Oracle propotypes,这是为什么,是因为这些样本跑掉了吗?还是说处于了一个边界点上。
值得实验和思考的点
Corrected Prototypes (p_corrected) 的性能显著优于 Naive Prototypes,并且接近于 Oracle Prototypes 的表现,这表明大部分漂移可以通过 LDC 进行有效补偿,从而减轻灾难性遗忘。示意图如下图所示
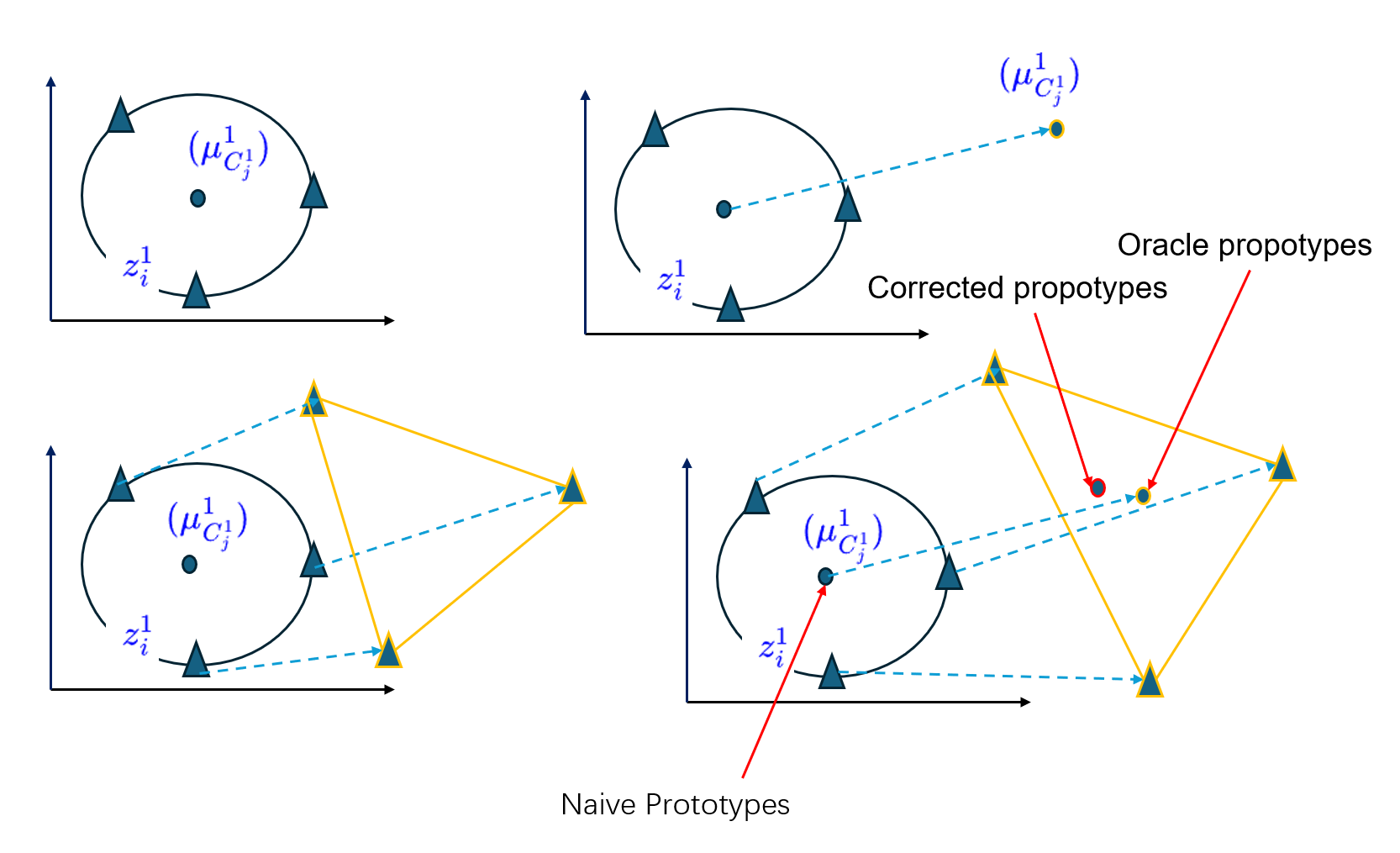
从实验结果来看,真正的类原型还是有作用的,作者提出的LDC方法也有很好的效果。所以整体的思路是可行的。
SDC,ADC 设置的缺点
作者接着提出,SDC,ADC的做法可能是有问题的,在一些情形下会失效。
现有的一些漂移补偿方法,比如语义漂移补偿(Semantic Drift Compensation, SDC),主要依赖于对漂移的局部线性近似,即假设漂移可以通过平移来捕捉。这意味着它们在计算新任务数据的特征漂移时,认为每个特征的漂移是简单的平移变换。这种假设在一些情况下可能是合理的,但它并不能涵盖所有的漂移类型,尤其是那些更为复杂的变换(如缩放和旋转)。
当漂移并非单纯的平移,而是涉及更复杂的变换(例如旋转和缩放)时,SDC 方法对特征漂移的估计会出现显著的偏差。这意味着在面对这种复杂漂移时,SDC 方法不能有效地补偿旧类原型的位置,从而导致较差的分类性能。
作者通过一个二维的示例来说明这一局限性:
他们对三个样本分布分别进行了平移、旋转和缩放等不同类型的变换,并试图估计这些样本在新任务中的漂移。
当仅仅应用平移时,SDC 能够很好地估计分布的漂移,即它可以准确地找到旧类原型的新位置。
但是,当涉及旋转和缩放等更复杂的变换时,SDC 对漂移的估计则出现了明显的偏差。这种偏差会使得估计的类原型位置远离其实际的位置,导致分类性能下降。

在面对上述复杂漂移时,论文中提出的Learnable Drift Compensation (LDC) 方法显示出显著的优势。LDC 使用了一个可学习的映射器(projector),可以在训练中灵活地调整和学习如何补偿特征空间的漂移,而不对漂移的性质作出固定假设。因此,LDC 可以处理各种类型的漂移,包括平移、旋转、缩放等,使得它在补偿旧类原型的漂移时更加准确。
这部分内容的核心是指出传统的SDC 方法的局限性在于它对漂移类型的假设过于简单,仅限于平移,导致在复杂的漂移情况下效果不佳。而LDC 方法则通过引入一个可学习的映射器,使得模型能够灵活适应多种类型的漂移,从而有效改善持续学习中的性能。这也是为什么 LDC 能在实验中显著优于 SDC 的原因之一。
解决应当如何提升,解决呢
上面已经说了这么多 LDC的优点,那LDC 所谓的 一个可以学习的映射到底是怎样的呢?它和SDC有什么区别,和上面的MAE又有什么区别?
首先,LDC是一个映射的神经网络,其做法和上面的MAE类似,都是学习一个从上一个特征空间到下一个特征空间的映射,我们还是以任务1,任务2为例子,目的就是学习到一个特征空间之间的映射,
在完成训练任务 $1$ 之后,得到了模型$M^1$, 这包括特征提取器 $MS^1$ 和 $MC^1$。 然后继续进行任务 $2$ , 此时有着数据 $x^2 \in D^2$。然后继续进行任务 $2$ , 完成训练之后,能够获得 到了模型$M^2$, 这包括特征提取器 $MS^2$ 和 $MC^2$。 这里的模型是一个神经网络,也可以理解为是一个函数变换。
将特征空间 $Z^1$ 转换到 特征空间 $Z^2$ ,我们将其称之为 特征空间变化网络 ,
\[\begin{aligned} f^{t-1 \rightarrow t} &: Z^1 \rightarrow Z^2 \\ f^{1 \rightarrow 2} &: MS^1(x^1_i) \rightarrow MS^2(x^1_i) \\ MS^2(x^1_i) &= f^{1 \rightarrow 2}(MS^1(x^1_i)) \end{aligned}\]同样的,类似SDC的做法,无法得到任务一的数据 ,但是可以有着任务 $2$ 的数据 $x^2_i \in D ^2$ , 于是
\[\begin{aligned} f^{1 \rightarrow 2'} &: MS^1(x^2_i) \rightarrow MS^2(x^2_i) \\ z^2_i &= f^{1 \rightarrow 2'}(z^2_i)\\ MS^2(x^2_i) &= f^{1 \rightarrow 2'}(MS^1(x^2_i)) \end{aligned}\]上面两个的差别只是输入不同,根据泛函,两个函数之间也可以定义函数,即只要有
\[F^{1 \rightarrow 2} : MS^1 \rightarrow MS^2\]泛函存在,那么上述关系就能成立 ,这里的 $F$ 和上面的 $f$是一个吗?好像不是一个
$f^{1 \rightarrow 2}$ 作用于单个特征向量(如 $MS^1(x)$),描述的是如何将任务 1 中的特征映射到任务 2 中的特征。
$F^{1 \rightarrow 2}$ 是作用在整个特征提取器上的泛函,描述的是如何将特征提取器 $MS^1$ 转变为 $MS^2$。
第一个 $f^{1 \rightarrow 2} : MS^1(x^1_i) \rightarrow MS^2(x^1_i)$ 实际上还是两个特征向量之间的函数关系,其定义域为 训练任务一的所有训练数据 $x^1$ 经过函数 $MS^1$得到的 特征向量 $z^1$ 所形成的空间$Z^1$, 其值域为 训练任务一的所有训练数据 $x^1$ 经过函数 $MS^2$得到的 特征向量 $z^2$ 所形成的空间$Z^2$ ,
第二个 $f^{1 \rightarrow 2’} : MS^1(x^2_i) \rightarrow MS^2(x^2_i)$ 实际上还是两个特征向量之间的函数关系,其定义域为 训练任务二的所有训练数据 $x^2$ 经过函数 $MS^1$得到的 特征向量 $z^1$ 所形成的空间$Z^1$, 其值域为 训练任务一的所有训练数据 $x^2$ 经过函数 $MS^2$得到的 特征向量 $z^2$ 所形成的空间$Z^2$ ,
但这两个$f^{1 \rightarrow 2}$是不是两个是一样的呢?
- 特征提取器 $MS^1$ 和 $MS^2$:
- 由于模型 $M^2$ 是在模型 $M^1$ 的基础上,通过任务 2 的数据 $D^2$ 训练得到的,因此 $MS^1$ 和 $MS^2$ 应该是同一个特征提取器结构,只是在不同的任务上可能经过了微调。
- 也就是说,$MS^2$ 基于任务 2 数据集 $D^2$ 对 $MS^1$ 进行了进一步优化,调整了权重,但特征提取器的核心框架和功能是共享的。
分析两个 $f^{1 \rightarrow 2}$:
- 第一个 $f^{1 \rightarrow 2} : MS^1(x^1_i) \rightarrow MS^2(x^1_i)$:
- 定义域:任务 1 的数据 $x^1_i$ 经过 $MS^1$ 提取的特征,形成特征空间 $Z^1$。
- 值域:任务 1 的数据 $x^1_i$ 经过 $MS^2$ 提取的特征,形成特征空间 $Z^2$。
- 作用:这个 $f^{1 \rightarrow 2}$ 描述的是如何将任务 1 的特征(由 $MS^1$ 提取)映射到任务 2 中调整后的特征(由 $MS^2$ 提取),捕捉的是模型从任务 1 到任务 2 学习过程中的变化。
- 第二个 $f^{1 \rightarrow 2’} : MS^1(x^2_i) \rightarrow MS^2(x^2_i)$:
- 定义域:任务 2 的数据 $x^2_i$ 经过 $MS^1$ 提取的特征,形成的特征空间 $Z^1$。
- 值域:任务 2 的数据 $x^2_i$ 经过 $MS^2$ 提取的特征,形成的特征空间 $Z^2$。
- 作用:这个 $f^{1 \rightarrow 2}$ 描述的是任务 2 的数据如何通过 $MS^1$ 的特征提取器映射到 $MS^2$ 中的特征,反映了在任务 2 数据集上的特征转换。
是否相同的判断:
现在的问题是,这两个 $f^{1 \rightarrow 2}$ 是否相同?既然 $MS^1$ 和 $MS^2$ 是在任务 1 和任务 2 上共享相同的模型框架,区别只是任务 2 通过数据 $D^2$ 对模型进行微调,因此我们需要考虑以下几点:
- 特征提取器的共享性:
- 既然 $MS^1$ 和 $MS^2$ 是在相同的特征提取器基础上,通过任务 2 的数据进行微调得到的,那么理论上 $MS^1$ 和 $MS^2$ 的转换应该是紧密相关的。即使它们在任务 2 上经过了一定的调整,$MS^1$ 和 $MS^2$ 的输出特征也会有高度相关性。
- 输入数据的不同:
- 尽管 $MS^1$ 和 $MS^2$ 是相同的模型,但输入数据不同。第一个 $f^{1 \rightarrow 2}$ 是基于任务 1 的数据 $x^1_i$,第二个 $f^{1 \rightarrow 2’}$ 是基于任务 2 的数据 $x^2_i$。任务 1 和任务 2 的数据分布可能存在差异,因此,$MS^1$ 对不同任务的数据提取的特征(即 $MS^1(x^1_i)$ 和 $MS^1(x^2_i)$)可能不完全相同。
- 任务 1 和任务 2 的数据差异意味着即使 $MS^1$ 和 $MS^2$ 的结构相同,但由于输入数据的不同,两个特征向量的分布可能会不同,这会导致 $f^{1 \rightarrow 2}$ 的表现有所差异。
结论:
- 理论上,由于 $MS^1$ 和 $MS^2$ 是在同一个模型架构下微调得到的,它们的特征映射关系 $f^{1 \rightarrow 2}$ 在两个不同数据集 $x^1$ 和 $x^2$ 上的表现应该是非常相似的。
- 实际上,由于任务 1 和任务 2 的输入数据分布不同,$MS^1$ 提取的特征可能会有所不同,进而影响 $f^{1 \rightarrow 2}$ 的具体映射结果。因此,虽然这两个 $f^{1 \rightarrow 2}$ 具有相同的形式和目标,但它们在不同数据上的表现可能略有差异。
因此,这两个 $f^{1 \rightarrow 2}$ 在形式上相同,但由于输入数据的不同,它们的具体映射可能略有不同。在持续学习的框架下,任务 2 的训练数据 $D^2$ 会对 $MS^2$ 的微调产生影响,进而导致两个 $f^{1 \rightarrow 2}$ 的映射结果可能存在一些细微的区别。
我们可以进行实验验证这个事情!!!!!
只要 $x^1_i , x^2_i$ 两个不同的向量来自同一个空间(或者分布,比如同一个$n$ 维实数向量空间,或者相同的图片类别 如小狗和小猫),其通过同一个函数 $MS^1, MS^2$ 映射的结果就是同一个空间 (或者分布,比如同一个$m$ 维实数向量空间)吗?
在任务一和任务二中,即使两个输入向量 $x^1_i$ 和 $x^2_i$ 都来自同一个 $n$ 维实数向量空间(比如 $\mathbb{R}^n$,它们的维度是相同的),由于它们分别代表不同类别的对象(如任务一的向量 $x^1_i$ 代表猫的图片,任务二的向量 $x^2_i$ 代表飞机的图片),它们通过同一个特征提取器 $MS^1$ 的映射结果可能会有以下几方面的区别:
1. 映射结果是否在同一个空间
是的,即使 $x^1_i$ 和 $x^2_i$ 来自不同的数据分布,且表示不同类型的对象,它们经过同一个函数 $MS^1$ 映射之后的结果依然位于同一个输出空间。因为:
\[MS^1 : \mathbb{R}^n \to \mathbb{R}^m\]
- $MS^1$ 是一个从 $n$ 维空间 $\mathbb{R}^n$ 映射到 $m$ 维空间 $\mathbb{R}^m$ 的函数,即:
- 无论输入 $x^1_i$ 和 $x^2_i$ 是什么,它们的维度都是 $n$,并且都被映射到同一个输出空间 $\mathbb{R}^m$。
2. 映射结果的区别
尽管映射的结果仍在同一个空间 $\mathbb{R}^m$,但由于 $x^1_i$ 和 $x^2_i$ 分别来自不同的数据分布(猫的图片和飞机的图片),其映射结果在这个 $m$ 维空间中的具体位置和分布可能会有显著差异。原因如下:
- 输入数据的分布差异:任务一中的数据(比如猫的图片)和任务二中的数据(比如飞机的图片)可能在特征空间中表现出完全不同的模式。虽然 $MS^1$ 的函数形式相同,但它提取的特征反映的是输入数据的结构和分布。因此,任务一的输入 $x^1_i$ 和任务二的输入 $x^2_i$ 会被映射到输出空间中不同的位置。
- 猫的图片可能会映射到特征空间的某一部分,而飞机的图片则会映射到特征空间的另一部分。
- 特征的语义差异:$MS^1$ 提取的特征本质上是对输入数据的某些语义或统计模式的表达。如果 $MS^1$ 是一个用于图像处理的神经网络,猫的图片和飞机的图片可能具有完全不同的边缘特征、纹理模式等。因此,特征提取器 $MS^1$ 从这两类数据中提取的特征会有较大差异,最终映射结果在 $m$ 维空间中会位于不同的区域。
3. 映射结果的分布差异
- 簇分布:在特征空间 $\mathbb{R}^m$ 中,来自任务一的数据 $x^1_i$ 可能会在某个区域聚集,而任务二的数据 $x^2_i$ 会在特征空间中的另一部分形成一个新的簇。这种聚类现象反映了不同类别的数据在特征空间中的分布差异。
- 任务的分离性:由于 $x^1_i$ 和 $x^2_i$ 分别代表不同的物体(猫和飞机),理想情况下,特征提取器 $MS^1$ 应该能够在特征空间中将这两类数据分开。这意味着尽管映射结果都位于 $\mathbb{R}^m$ 中,但猫和飞机的特征应该位于不同的子空间或区域。
4. 映射空间中的可区分性
虽然输入的向量 $x^1_i$ 和 $x^2_i$ 来自同一个 $n$ 维实数向量空间,但 $MS^1$ 的设计(比如神经网络)旨在提取有助于分类或区分不同类别的特征。因此,猫的特征和飞机的特征在经过 $MS^1$ 之后应该具有高可区分性,这反映为它们在特征空间 $\mathbb{R}^m$ 中的分布明显不同。
结论:
- 相同的输出空间:无论任务一和任务二的数据如何不同,由于它们都经过同一个特征提取器 $MS^1$,映射结果依然位于同一个 $m$ 维实数向量空间 $\mathbb{R}^m$。
- 不同的分布模式:尽管映射结果在同一个空间中,但由于输入数据的分布和类别不同,任务一(猫图片)和任务二(飞机图片)的映射结果在特征空间 $\mathbb{R}^m$ 中会有不同的分布模式,可能会形成不同的簇或位于不同的子区域。
还是说是依赖于 $MS$ 的具体形式?如果说是同一个空间,那么 $MS^2(x^1_i),MS^2(x^2_i)$岂不是就可以直接用同一个度量来进行刻画,这也就是SDC的思路。如果是不同的空间,那么上面的两个变换岂不是不同的,那也就没法相互替代。
不对,即使是同一个空间,但是不同的分布,结果依旧是不一样的。由于 神经网络的映射结果通常是一个高维度的空间,其子分布可能是不同维度下的子空间,
有了上述的变换关系$f^{1\rightarrow 2}$之后,就可以得到变换下的 类原型
\[\mu^2_{c^1_j} = f^{1 \rightarrow 2} (\mu^1_{c^1_j})\]这个等式成立吗? 其核心是
\[\begin{aligned} f^{1 \rightarrow 2} (\mu^1_{c^1_j}) &= f^{1 \rightarrow 2} (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^1_i )\\ &= f^{1 \rightarrow 2} (\frac{\sum_{i} [y_i = c^1_j] MS^1(x^1_i)} {\sum_{i} [y_i = c^1_j]} )\\ \\ & \text{If this hold on } f(a+b) = f(a)+f(b) : \text{可加性}\\ \\ & = \frac{\sum_{i} [y_i = c^1_j]f^{1 \rightarrow 2}( MS^1(x^1_i))} {\sum_{i} [y_i = c^1_j]} \\ & \text{If this hold on }MS^2(x^1_i) = f^{1 \rightarrow 2}(MS^1(x^1_i)) \\ &\text{注意是来自第一个任务的数据}x^1_i \text{与对应的变换}f^{1 \rightarrow 2}\\ & = \frac{\sum_{i} [y_i = c^1_j]( MS^2(x^1_i))} {\sum_{i} [y_i = c^1_j]} \\ & = \mu^{2}_{c^1_j} \end{aligned}\]注意上述使用了 全部都是 $x^1_i$ 且对应的 $f^{1\rightarrow 2}$。
如果是文中的表述,则有下面的表述 其中进行了函数的替换和样本数据的替换,进行了两个类似
\[\begin{aligned} f^{1 \rightarrow 2} (\mu^1_{c^1_j}) &= f^{1 \rightarrow 2} (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^1_i )\\ &= f^{1 \rightarrow 2} (\frac{\sum_{i} [y_i = c^1_j] MS^1(x^1_i)} {\sum_{i} [y_i = c^1_j]} )\\ \\ & \text{If this hold on } f(a+b) = f(a)+f(b) : \text{可加性}\\ \\ & = \frac{\sum_{i} [y_i = c^1_j]f^{1 \rightarrow 2}( MS^1(x^1_i))} {\sum_{i} [y_i = c^1_j]} \\ & \text{If this hold on }MS^2(x^1_i) = f^{1 \rightarrow 2}(MS^1(x^1_i)) \\ &\text{注意是来自第一个任务的数据}x^1_i \text{与对应的变换}f^{1 \rightarrow 2}\\ & = \frac{\sum_{i} [y_i = c^1_j]( MS^2(x^1_i))} {\sum_{i} [y_i = c^1_j]} \\ & = \mu^{2}_{c^1_j} \end{aligned}\]我们按着上述的推导再来看一下, 其中 $n_c$ 是属于类 $c$ 的样本数
| $MS^2(x^2)={z | z= MS^2(x^2_i),x^2 \in D^2}$ |
放弃这个我们继续从坐标推导
\[\begin{aligned} f^{1 \rightarrow 2} (\mu^1_{c^1_j}) &= f^{1 \rightarrow 2} (\frac{1}{n_c} \sum_{i} [y_i = c^1_j] z^1_i )\\ &= f^{1 \rightarrow 2} (\frac{\sum_{i} [y_i = c^1_j] MS^1(x^1_i)} {\sum_{i} [y_i = c^1_j]} )\\ \\ & \text{If this hold on } f(a+b) = f(a)+f(b) : \text{可加性}\\ \\ & = \frac{\sum_{i} [y_i = c^1_j]f^{1 \rightarrow 2}( MS^1(x^1_i))} {\sum_{i} [y_i = c^1_j]} \\ & \text{If this hold on } f(a+b) = f(a)+f(b) : \text{可加性}\\ & = \frac{\sum_{i} [y_i = c^1_j]( MS^2(x^1_i))} {\sum_{i} [y_i = c^1_j]} \\ & = \mu^{2}_{c^1_j} \end{aligned}\]$f(\sum(a)) = \sum(f(a))$
文档信息
- 本文作者:zuti666
- 本文链接:https://zuti666.github.io/2024/09/20/Paper-Reading-Note-2-SDC-ADC-LDC/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)