MMD–On the Exploration of Incremental Learning for Fine-grained Image Retrieval

论文信息

On the Exploration of Incremental Learning for Fine-grained Image Retrieval

设定

本文研究了在增量设置下，细粒度图像检索（Fine-grained Image Retrieval, FGIR）的问题。当新类别随着时间的推移不断加入时，如何在不访问原始类别样本的情况下进行有效的增量学习，同时防止遗忘原有类别的知识。

在现实应用中，图像数据和类别的数量不断增加。传统的图像检索方法通常基于静态数据集，无法适应不断增加的新类别。当模型对所有类别进行联合训练时，可以保证性能，但这种重复训练过程非常耗时。另一方面，仅对新类别进行微调会导致“灾难性遗忘”问题，即模型会忘记对原始类别的良好性能。因此，本文提出了一种增量学习方法，以缓解由于遗忘问题导致的检索性能下降。

创新点

本文的创新点在于提出了一种适用于细粒度图像检索（FGIR）的增量学习框架，能够有效应对新类别的逐步加入，同时防止“灾难性遗忘”原始类别。具体来说，创新点包括：

1. 无样本增量学习: 本文的方法在学习新类别时不访问任何原始类别的样本，这解决了由于隐私问题或存储限制而无法访问原始数据的现实问题。
2. 知识蒸馏结合最大均值差异（MMD）: 提出了基于知识蒸馏和MMD的双重正则化策略，知识蒸馏用于保持分类器输出的一致性，MMD用于最小化特征分布差异，从而在增量学习过程中保持良好的检索性能。
3. 细粒度图像检索的增量学习: 该方法首次将增量学习应用于细粒度图像检索，展示了其在处理细微类别差异方面的优势。

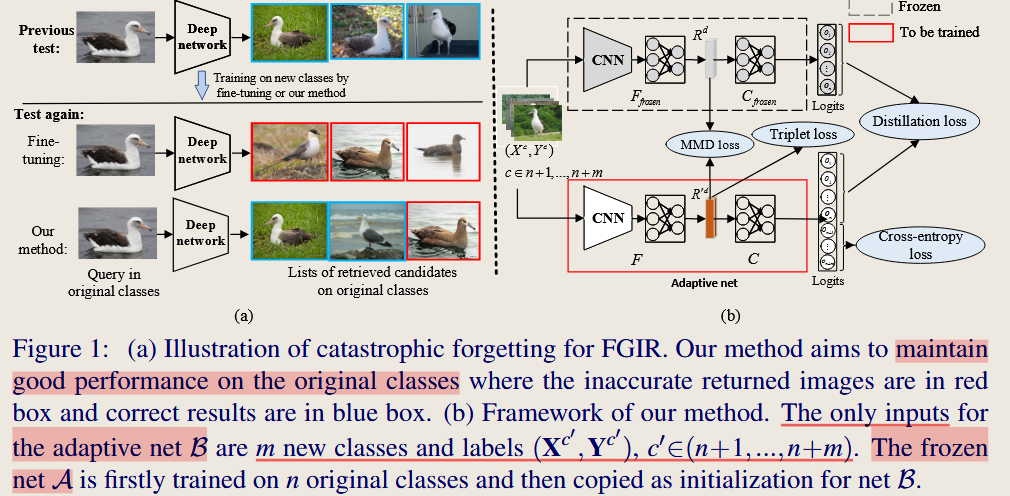
方法设计思想

该方法的设计思想是通过联合使用知识蒸馏和MMD正则化，来同时实现对新类别的适应能力和对原始类别的记忆保留。具体来说：

• 知识蒸馏: 将原始网络的软标签作为监督信号，用于训练新的适应性网络，确保新网络在增量训练过程中不会过多地偏离原始网络的决策边界。
• MMD正则化: MMD用于在特征空间中度量原始网络和新网络之间的分布差异，最小化该差异能够保持新网络与原始网络在特征表示上的一致性，从而缓解遗忘问题。

原理与技术细节

Semantic Preserving Loss

Semantic Preserving Loss 通过交叉熵损失和三元组损失来捕捉类别间的语义特征，确保新旧类别之间的特征保持一致，从而减少遗忘效应。

交叉熵损失

交叉熵损失（Cross-Entropy Loss）用于分类任务，通过最小化预测值与真实标签之间的距离来训练模型。假设模型的输出 logits 为 $(o_1, o_2, \dots, o_n)$，真实的类别标签为 $(y_1, y_2, \dots, y_n)$，则交叉熵损失公式如下：

其中，$N$ 是样本数，$y_i$ 是第 $i$ 个样本的标签，$o’_i(x)$ 是该样本通过网络后的预测值的 logits，$n+m$ 表示新旧类别的总数。

log 后面的是一个softmax 函数. Softmax 函数的主要作用是将模型输出的 logits 转换成可以理解为概率的数值，这些概率反映了样本属于不同类别的可能性。Softmax 的公式如下：

其中：

• $p_i$ 是第 $i$ 类的预测概率；
• $o_i$ 是模型在第 $i$ 类上的输出（logit 值）；
• $n+m$ 是类别的总数（$n$为原始类别数，$m$为新增类别数）。

Softmax 通过计算各类 logit 值的指数并对它们求和来进行归一化处理，保证输出的概率总和为 1

注意由于增量学习中的数据访问限制设定，无法得到之前的数据，因此这里仅使用新的类别的图像的数据。这个也就是要求 新类别的数据能够被正常分类。

三元组损失

为了更好地区分细粒度类别，采用了三元组损失（Triplet Loss）。三元组损失提高了特征向量的判别性。

三元组损失通过“难正样本对”（hard positive pairs）和“难负样本对”（hard negative pairs）来优化模型，使得相同类别的样本之间距离更近，不同类别的样本之间距离更远。其公式如下：

其中，$S_{i, \text{neg}}$ 表示第 $i$ 个样本与难负样本之间的相似度，$S_{i, \text{pos}}$ 表示该样本与难正样本之间的相似度，$\lambda$ 是用于区分正负样本的边界阈值。

知识蒸馏损失（Distillation Loss）

原理: 知识蒸馏旨在将原始网络（教师网络）中的知识转移到新的适应性网络（学生网络），通过使得学生网络的输出与教师网络的输出接近，从而保持对原始类别的识别能力。

技术细节:

• 定义原始网络的输出 logits 为 $(o_1, o_2, \ldots, o_n)$，适应性网络的输出为 $(o’1, o’_2, \ldots, o’_n, o’{n+1}, \ldots, o’_{n+m})$。

• 蒸馏损失定义为：

$T$ 为温度参数，通常设为2。

最大均值差异损失（MMD Loss）

原理: 目的是减少新模型与原模型在特征分布上的差异。MMD用于衡量两个特征分布之间的距离，通过最小化新网络与冻结网络（即原始网络）特征分布的MMD，保了新模型的特征分布尽可能与原模型的特征分布相近，从而保留原模型的特征信息。

技术细节:

给定来自原始网络和新网络的特征向量集合 $R$ 和 $R’$，MMD计算特征分布均值之间的距离：

其中，$R$ 和 $R’$ 是两组样本的特征， $\phi(\cdot)$ 是将特征映射到再生核希尔伯特空间（RKHS）的函数， $\mathcal{H}$ 表示再生核希尔伯特空间（RKHS）。这里 $\phi$ 函数的作用是将原始的特征映射到一个高维的特征空间，在这个空间中进行均值计算和距离度量。

通过将平方展开并结合希尔伯特空间的性质，得到

在这个公式中，$\langle \phi(R_i), \phi(R_j) \rangle_{\mathcal{H}}$ 表示 $R_i$ 和 $R_j$ 在高维空间 $\mathcal{H}$ 中的内积。

为了简化计算，使用核技巧替代内积。 在实际操作中，直接计算 $\phi(R_i)$ 通常非常困难，因为 $\phi(\cdot)$ 通常是一个高维甚至无限维的映射。因此，无法直接在 $\mathcal{H}$ 中进行内积和距离计算。 核技巧的核心思想是，虽然我们无法明确计算出 $\phi(R_i)$，但我们可以通过核函数 $k(R_i, R_j)$ 间接计算出 $\phi(R_i)$ 和 $\phi(R_j)$ 在高维空间中的内积：

将核函数 $k$ 代入上面的公式后，MMD 损失可以表示为：

在论文中，作者采用了高斯核（Gaussian kernel）， 其形式为：

其中：

$ \vert R_i - R_j \vert^2$ 表示 $R_i$ 和 $R_j$ 之间的欧氏距离； $\sigma$ 是高斯核的参数，用来控制核函数的尺度。

最终得到 MMD 损失为：

其中，$k(R_i, R_j)$ 是核函数，它的输出是 $\phi(R_i)$ 和 $\phi(R_j)$ 在高维空间中的内积值，而不需要显式地计算 $\phi(R_i)$ 和 $\phi(R_j)$。$k(R, R’) = \exp\left(-\frac{|R - R’|^2}{2\sigma^2_m}\right)$，$\sigma_m$ 是高斯核中的方差。

总体损失函数

综合考虑多个损失函数，构建一个整体目标函数，以平衡新旧类别之间的性能。

技术细节:

最终的目标函数为：

其中，$\alpha$ 和 $\beta$ 是权衡参数，

$L_{\text{ce}}$ 为交叉熵损失，$L_{\text{triplet}}$ 为三元组损失， 描述了新添加的样本的正确识别和分类效果。交叉熵损失 和 三元组损失 则用于训练模型识别新类别，并提升其在新类别上的性能。

$L_{\text{dist}}$ 是为了将新旧模型的输出进行对齐， $L_{\text{mmd}}$ 是为了将新旧模型的特征空间进行对齐，负责保持对原有类别的知识和特征分布，防止模型在学习新类别时遗忘旧类别。

$\alpha L_{\text{dist}} + \beta L_{\text{mmd}}$ 描述了将新旧模型进行对齐的设置，分别是输出和特征两方面进行对齐，此外还设置了参数来权衡这两方面的重要性

思考与疑问

这里使用MMD Loss 来进行衡量新模型与原模型在特征分布上的差异，这是基于最终输出分布结果的差异进行衡量的，那使用其他类似的方法。这里提到的特征之间的差异，通常是指同一个输入样本在新模型和旧模型中的特征向量需要尽可能一致。也就是说，对于同一个输入数据（例如一张图片或一个文本），新模型所提取的特征表示（特征向量）应该与旧模型提取的特征表示尽量相似，以保持特征空间的一致性。通过让同一个输入样本的特征向量在新旧模型中保持一致，可以有效避免增量学习中的灾难性遗忘，并确保新旧模型在同一特征空间中工作，从而保持向后兼容性。

除了 MMD Loss（Maximum Mean Discrepancy Loss） 用于衡量新模型与原模型在特征分布上的差异外，以下是几种常用的其他方法，它们在增量学习和特征对齐问题中广泛使用，可以有效地衡量新旧模型的特征分布差异：

1. 知识蒸馏（Knowledge Distillation）

知识蒸馏是衡量新旧模型特征分布差异的经典方法。最初由 Hinton 等人提出，用于将大模型的知识提取到小模型中。增量学习中的知识蒸馏是通过保持新模型与旧模型在相同输入下的输出相似来防止灾难性遗忘。

公式：

其中：

• $p_{old}(x_i)$ 是旧模型对于输入 $x_i$ 的输出概率分布；
• $p_{new}(x_i)$ 是新模型的输出概率分布；
• $\text{KL}(\cdot)$ 是 KL 散度，用于衡量两个概率分布之间的差异。

优点：

• 简单高效：不需要额外的复杂计算，直接使用新旧模型的输出进行对齐；
• 广泛应用：知识蒸馏在各种增量学习场景中都非常有效，特别是在保持新旧模型的特征一致性方面。

缺点：

• 对概率输出敏感：蒸馏过程中对于输出的精确匹配可能不总是最佳的，尤其是当特征表示空间较为复杂时。

2. 对抗性特征对齐（Adversarial Feature Alignment）

对抗性学习是另一种用于对齐新旧模型特征分布的常用方法。通过引入一个对抗性网络来判断特征是来自新模型还是旧模型，从而引导新模型的特征分布向旧模型的特征分布靠近。

主要机制：

• 训练一个判别器，区分特征是否来自旧模型；
• 通过对抗性损失，优化新模型使得其生成的特征不能被判别器区分，从而实现特征对齐。

对抗性损失函数：

其中：

• $D(\cdot)$ 是判别器；
• $f_{new}(x_i)$ 和 $f_{old}(x_i)$ 分别是新模型和旧模型的特征表示。

优点：

• 强大的特征对齐能力：对抗性机制能够在复杂分布中有效对齐特征分布；
• 灵活性：可以应用在多种不同类型的任务中（如分类、检索等）。

缺点：

• 训练复杂：需要训练额外的判别器，并且容易导致训练不稳定（如模式崩溃等）。

3. 基于特征重放的增量学习（Feature Replay）

特征重放是一种类似经验重放的技术，但不同之处在于它重放的是旧模型生成的特征，而不是直接重放原始数据。这种方法通过保留一些旧模型的特征，强制新模型的特征与旧特征保持一致。

机制：

• 保留一些旧任务的数据或特征；
• 在训练新任务时，将这些旧任务的特征作为约束，让新模型尽量保持旧任务的特征一致性。

公式：

优点：

• 减少灾难性遗忘：特征重放能够显著减少新任务对旧任务知识的破坏；
• 数据效率高：相比直接重放原始数据，特征重放的存储和计算开销较小。

缺点：

• 特征选择依赖性：需要选择适当的特征来重放，特征选择不当可能影响模型的效果。

4. 投影对齐（Projection Matching）

投影对齐是一种直接通过投影矩阵将新旧特征进行对齐的方法。假设新模型和旧模型在不同的特征空间中工作，投影对齐通过一个投影矩阵将新模型的特征空间映射到旧模型的特征空间中，从而保持特征一致性。

公式：

其中 $P$ 是一个投影矩阵，将新模型的特征映射到旧模型的特征空间中。

优点：

• 显式对齐：通过投影的方式可以显式地对齐特征空间，较为直观；
• 灵活应用：可以在不同的特征空间之间进行转换。

缺点：

• 可能会丢失信息：如果投影矩阵的设计不合理，可能会丢失部分新模型的特征信息。

5. 基于层级的特征对齐（Layer-wise Feature Alignment）

在深度神经网络中，不同层次的特征可能有不同的分布。层级特征对齐通过逐层比较新旧模型相应层的特征分布，并使用损失函数将每一层的特征对齐，确保模型从低层到高层的特征都保持一致。

公式：

其中，$f_{new}^l(x_i)$ 和 $f_{old}^l(x_i)$ 分别是新模型和旧模型在第 $l$ 层提取的特征。

优点：

• 精细控制：可以在网络的不同层次精确控制特征对齐，提供更强的约束。

缺点：

• 计算复杂：需要计算多层的特征对齐，训练时计算量较大。

总结

除了 MMD Loss，知识蒸馏、对抗性特征对齐、特征重放、投影对齐和层级特征对齐等方法都是常用的衡量新旧模型特征分布差异的手段。这些方法各自有其优点和适用场景，可以根据具体任务需求和模型架构进行选择。

不同方法的权衡：

• 如果需要简单且高效的特征对齐，知识蒸馏是常用且稳健的选择；
• 如果特征分布较为复杂且需要强力对齐，对抗性特征对齐和 MMD Loss 是不错的选择；
• 特征重放适合于存储空间有限且希望减少灾难性遗忘的场景；
• 投影对齐和层级对齐适用于需要对不同特征空间进行显式处理的情况。