数据降维与可视化1 - PCA 主成分分析
参考链接
【机器学习】数据降维(Dimensionality Reduction) - 知乎
【数据降维-第1篇】主成分分析(PCA)快速理解,及MATLAB实现 - 知乎
潜在空间可视化:PCA、t-SNE、UMAP_哔哩哔哩_bilibili
(86 封私信 / 33 条消息) 如何通俗易懂地讲解什么是 PCA(主成分分析)? - 知乎
非数学解释与理解
想象一下,您刚刚开了一家苹果酒店。您有 50 种苹果酒,您想弄清楚如何将它们分配到货架上,以便将味道相似的苹果酒放在同一个货架上。苹果酒有很多不同的味道和质地——甜味、酸味、苦味、酵母味、果味、透明度、泡沫味等。因此,要将瓶子归类,您需要做的是回答两个问题:
1) 哪些品质对于识别苹果酒组最重要?例如,与根据果味分类相比,根据甜度进行分类是否更容易将苹果酒归类为味道相似的组别?
2) 我们可以通过组合其中一些变量来减少变量列表吗?例如,是否真的有一个变量是 “酵母度、净度和泡沫度 ”的某种组合,并且是分类品种的真正好的量表?
这本质上就是 PCA 所做的。主成分是有效解释数据集中变化的变量 - 在这种情况下,它们有效地区分了各组。每个主成分都是原始解释变量之一,或者是某些原始解释变量的组合。
主成分分析的目的就是要从这些现有的特征中重建新的特征,新的特征剔除了原有特征的冗余信息,因此更有区分度。注意,主成分分析的结果是得到新的特征(原有特征的线性组合),而不是简单地舍弃原来的特征列表中的一些特征。
- 新的特征拥有更好的区分度,转换成数学语言就是方差更大。
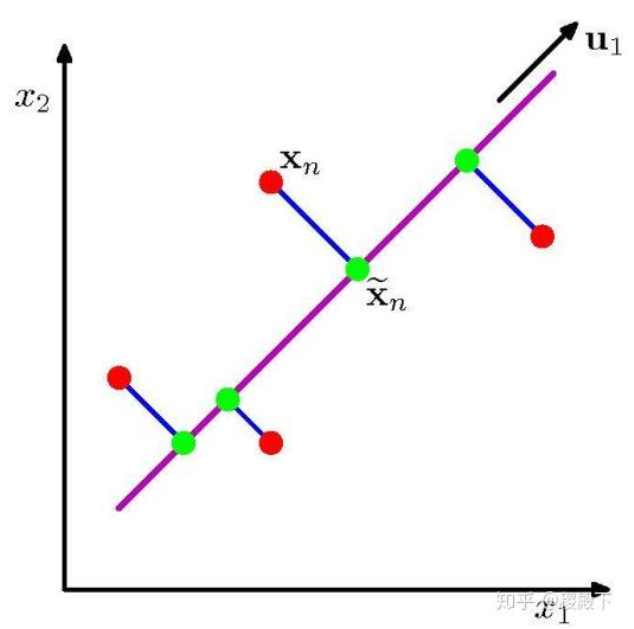
- 新的特征是原有特征的线性组合,它能够重建原有特征。主成分分析要保留最有可能重建原有特征的新特征,从而达到数据降维的作用。转换为数学语言就是投影误差最小。
动画理解
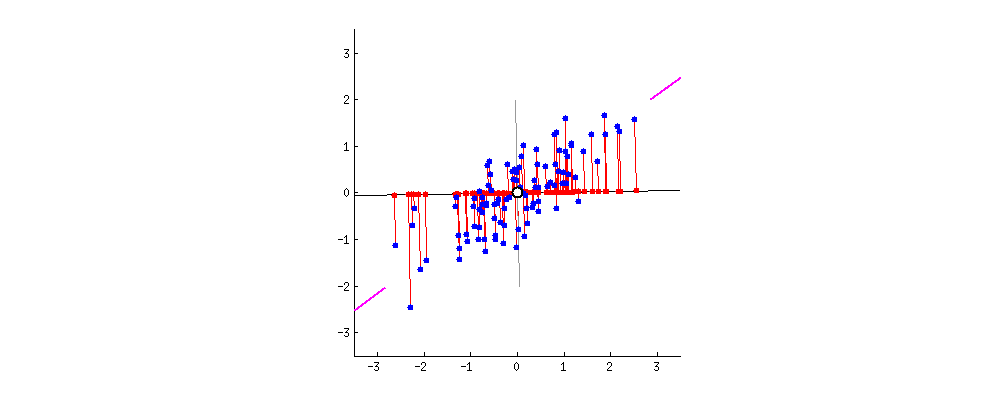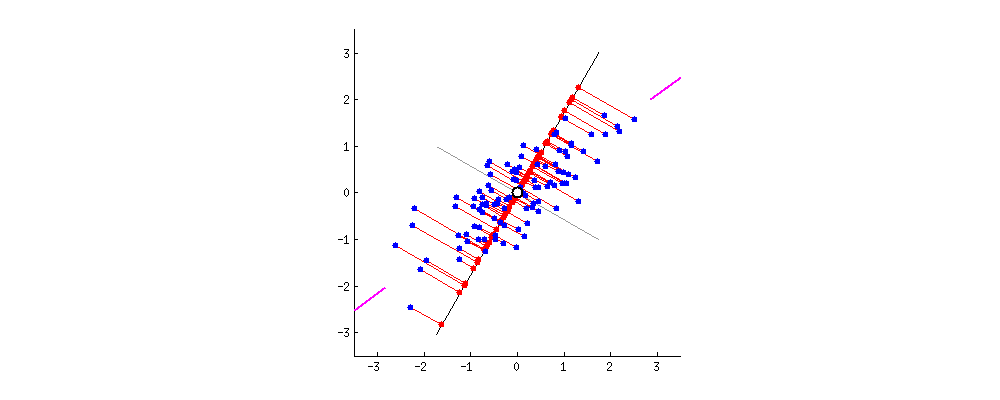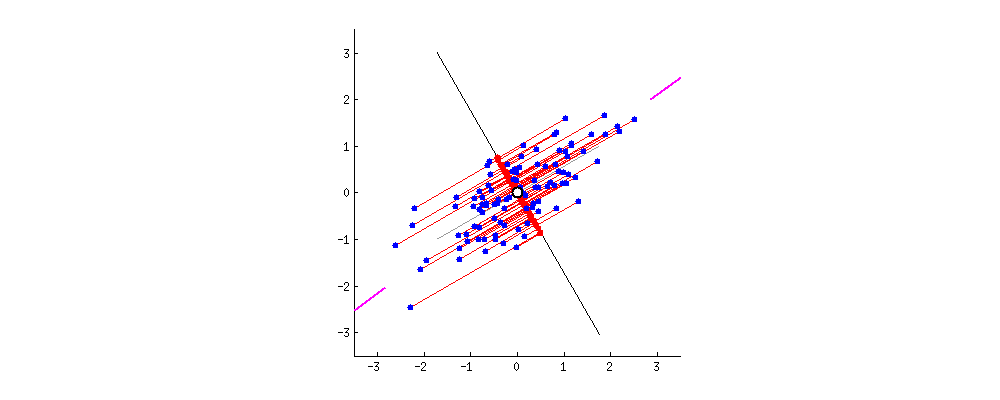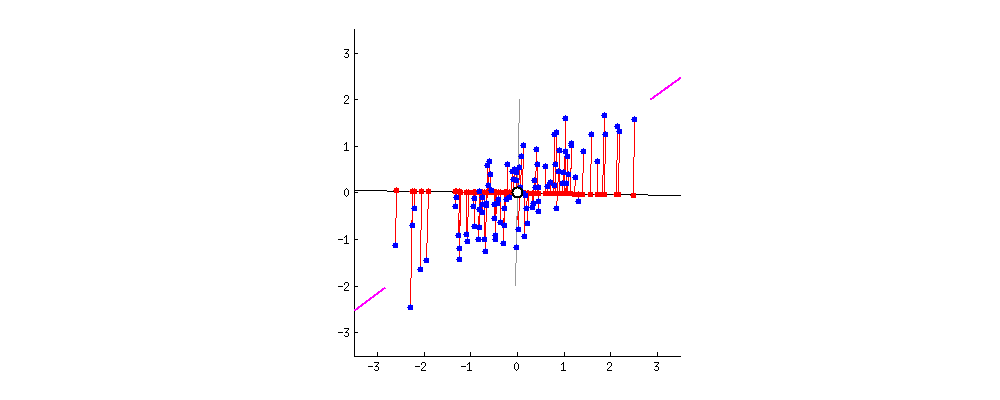
- 新的特征拥有更好的区分度,转换成数学语言就是方差更大。(动图中的黑色线上的点尽量不重合。)
- 新的特征是原有特征的线性组合,它能够重建原有特征。主成分分析要保留最有可能重建原有特征的新特征,从而达到数据降维的作用。转换为数学语言就是投影误差最小。(动图中黑色线与蓝点的连线的加和最小)
数学理解
【机器学习】数据降维(Dimensionality Reduction) - 知乎
文档信息
- 本文作者:zuti666
- 本文链接:https://zuti666.github.io/2024/11/09/%E6%95%B0%E6%8D%AE%E9%99%8D%E7%BB%B4%E4%B8%8E%E5%8F%AF%E8%A7%86%E5%8C%961-PCA/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)