Paper Reading 9 LLM- First-stage Retrieval L2R
论文信息
L2R: Lifelong Learning for First-stage Retrieval with Backward-Compatible Representations
AI总结
以下是对论文 《L2R: Lifelong Learning for First-stage Retrieval with Backward-Compatible Representations》 的详细分析:
研究范围与背景
论文聚焦于信息检索(Information Retrieval, IR)领域中 第一阶段检索 的挑战,特别是在动态和不断变化的数据环境中。目标是解决实际搜索场景中,由于文档持续新增导致的数据分布漂移问题。论文特别研究了在这种环境下的 持续学习(Lifelong Learning) 问题。
核心思想
提出了一种名为 L2R(Lifelong Learning for Retrieval) 的方法,旨在:
- 高效适应新数据,即使这些新文档是未标注的;
- 避免对已有文档的嵌入进行重复计算,确保向后兼容性(Backward Compatibility)。
研究方法
L2R 方法的核心包括:
- 记忆机制:存储历史数据以缓解遗忘问题;
- 数据选择策略:选择具有代表性的负样本以提升模型训练效果;
- 排序对齐目标:通过保持排名一致性,实现向后兼容性,同时减少计算成本。
关键技术:
- 支持负样本选择:从新数据中挑选有效的负样本进行训练。
- 排名对齐目标:确保模型在嵌入更新时保持旧数据的排名一致性。
- 基准测试:基于 LoTTE 和 Multi-CPR 数据集构建模拟真实场景的 LL-LoTTE 和 LL-MultiCPR 数据集。
主要贡献
- 任务形式化:首次将持续学习问题引入第一阶段检索任务,并定义了适用于未标注新文档的学习框架。
- 方法创新:提出了兼具有效性与效率的 L2R 方法,解决了数据漂移和向后兼容问题。
- 基准数据集:构建了 LL-LoTTE 和 LL-MultiCPR 两个新的基准,用于评估真实环境下的持续学习性能。
区别与创新
- 向后兼容性:与传统方法需要重新计算嵌入不同,L2R 确保旧数据嵌入无需更新。
- 排名对齐目标:通过松散的排名对齐目标取代严格的点对齐,提高模型对新数据的适应性。
- 记忆优化:优化记忆机制以存储多样化的负样本,提高模型对旧知识的保留能力。
实验结果与结论
L2R 在多个评测指标上显著优于基线方法(如 ER、MIR 和 OCS):
- 效果提升:在每个会话的召回率(R@100)和平均倒数排名(MRR)指标上均表现优异。
- 效率提升:通过向后兼容性机制减少嵌入计算成本,支持更大规模的文档集合。
- 兼容性:在保持性能的同时,实现了对新旧文档嵌入的无缝兼容。
与其他方法的对比
| 比较维度 | 传统方法 | L2R 方法 |
|---|---|---|
| 新数据处理 | 静态或代价高 | 高效的持续学习 |
| 兼容性 | 需要重新索引 | 嵌入向后兼容 |
| 计算效率 | 计算成本高 | 排名对齐目标优化,效率高 |
讨论
研究指出现有持续学习方法在信息检索任务中的局限性,尤其是处理动态和大规模文档集合的低效性。L2R 通过创新的负样本选择和排名对齐机制,显著提高了模型在动态环境下的适应能力。
证明结果
实验结果表明:
- 有效性:在 S@5、R@100 和 MRR 等指标上持续提升。
- 鲁棒性:比基线方法对分布漂移更具适应性。
- 效率:显著节省计算时间,同时维持或提升检索性能。
如果需要更具体的部分分析(例如方法或实验细节),请随时告知!
文中主要图表
AI 问答
问题三 文章算法的整体流程
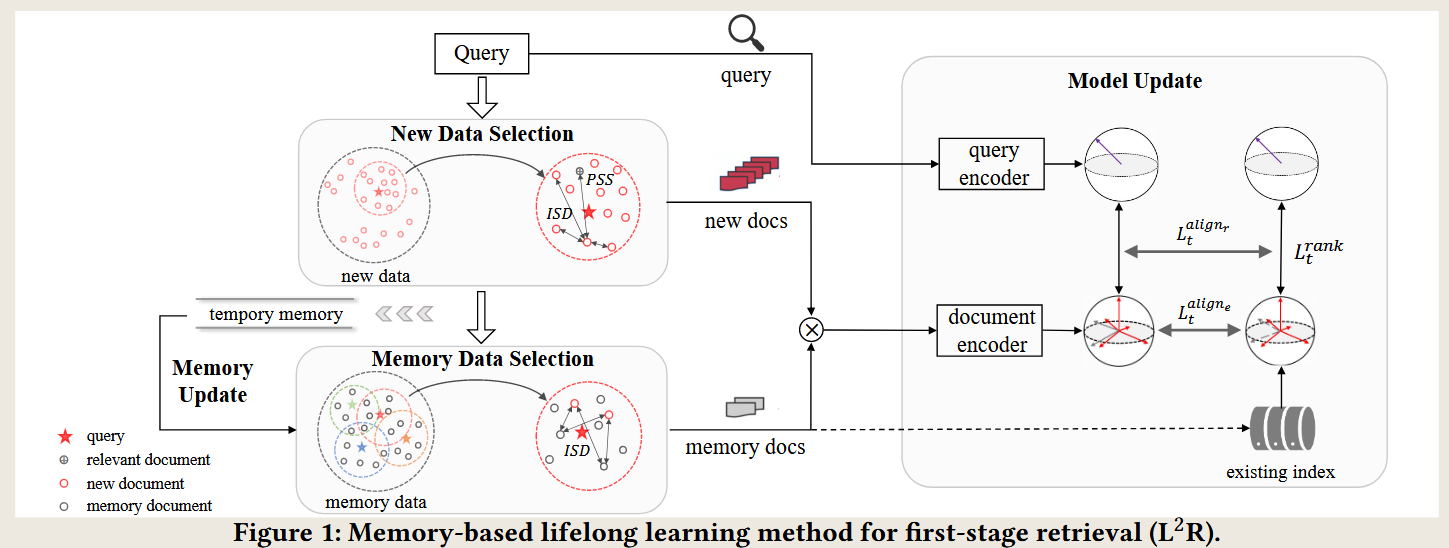
整体架构
论文的核心算法架构是一个面向持续学习(Lifelong Learning)的检索系统,旨在动态环境中解决文档分布漂移问题,同时实现向后兼容性(Backward Compatibility)。其架构主要包含以下模块:
- 新数据选择模块(New Data Selection):从新增文档中筛选出对模型学习有帮助的负样本。
- 记忆数据选择模块(Memory Data Selection):从历史记忆缓冲区中选取重要的旧样本,防止遗忘旧知识。
- 模型更新模块(Model Update):利用新旧样本更新模型,提升对新数据的适应性并维持对旧数据的兼容性。
- 记忆更新模块(Memory Update):更新记忆缓冲区,确保存储的样本多样且有代表性。
- 排序对齐目标(Ranking Alignment Objective):通过对排序结果的对齐,实现向后兼容性。
算法流程

论文提出了完整的 L2R 算法流程,其具体步骤如下:
输入与初始化
输入:
- 初始数据集 $C_0$:包含标注好的查询和相关文档对。
- 文档集合序列 ${D_0, D_1, \dots, D_T}$:每个会话(Session)中新增的未标注文档。
- 模型初始版本 $f_0$ 和记忆缓冲区 $M_0$。
输出:
- 更新后的检索模型 $f_T$,可对新旧文档进行高效检索。
算法步骤
1. 初始化
- 用 $C_0$ 训练初始模型 $f_0$,并将部分支持样本存储在记忆缓冲区 $M_0$。
2. 逐步处理每个会话的新数据
对于每个会话 $t \in {1, \dots, T}$,执行以下步骤:
步骤 1:新数据选择(New Data Selection)
目标:
- 从新增文档 $D_t$ 中选择具有代表性的负样本(支持负样本)。
操作:
使用 BM25 检索新文档集合 $D_t$,过滤掉明显不相关的文档,得到候选集合 $D_S^q$。
定义两个数据选择标准:
- 正样本优越性(Positive Sample Superiority, PSS):筛选可能是负样本的文档,避免将潜在正样本误作为负样本。
- 样本间多样性(Inter-Sample Diversity, ISD):确保选择的负样本分布广泛,减少冗余。
使用以下公式综合两者选择 $n_1$ 个新文档作为支持负样本: \(D_{\text{new}}^q = \arg\max_{d \in D_S^q} \alpha \cdot PSS(d, d_q^+) + (1 - \alpha) \cdot ISD(d, D_S^q)\)
步骤 2:记忆数据选择(Memory Data Selection)
目标:
- 从记忆缓冲区 $M_{t-1}$ 中选取重要的历史样本,与新数据结合,用于模型训练。
操作:
从缓冲区 $M_{t-1}$ 中筛选历史支持负样本。
使用 样本间多样性(ISD) 筛选 $n_2$ 个与新数据不同的样本,确保新旧样本的分布互补: \(D_{\text{mem}}^q = \arg\max_{d \in M_{t-1}} ISD(d, D_{\text{new}}^q)\)
步骤 3:模型更新(Model Update)
目标:
- 更新检索模型 $f_t$,使其适应新增数据,同时保持对旧数据的兼容性。
操作:
构建新的训练集,包含:
- 新数据中的负样本 $D_{\text{new}}^q$。
- 从记忆缓冲区选取的负样本 $D_{\text{mem}}^q$。
- 初始数据集 $C_0$ 中的正样本。
使用以下损失函数进行训练:
标准对比学习损失(若无需向后兼容性): \(L_{\text{no-com}} = -\log \frac{\exp(f_t(q, d_q^+))}{\sum_{d \in \{d_q^+\} \cup D_{\text{new}}^q \cup D_{\text{mem}}^q} \exp(f_t(q, d))}\)
向后兼容性损失:
排名对齐目标 $L_{\text{rank}}$:确保排序分布一致。
嵌入对齐目标 $L_{\text{align-e}}$ 或排名对齐目标 $L_{\text{align-r}}$: \(L_{\text{com}} = L_{\text{rank}} + \lambda \cdot L_{\text{align}}\)
步骤 4:记忆更新(Memory Update)
目标:
- 更新记忆缓冲区 $M_t$,以保存当前会话中重要的支持样本。
操作:
- 使用临时缓冲区 $M_c$ 保存当前会话中的新数据样本。
- 结合 $M_c$ 和旧缓冲区 $M_{t-1}$,根据样本多样性 $ISD$ 替换低优先级的旧样本,确保缓冲区内容保持新鲜且有效。
- 清空临时缓冲区,为下一会话准备。
算法终止
完成所有会话后,输出最终模型 $f_T$,此模型可兼容所有旧文档的嵌入,同时对新数据分布具有适应性。
每步目标总结
| 步骤 | 目标 |
|---|---|
| 新数据选择 | 从新文档中选取负样本,避免潜在正样本误选,并提升样本多样性。 |
| 记忆数据选择 | 从历史数据中选取关键样本,与新数据结合,防止遗忘旧知识。 |
| 模型更新 | 在不损害向后兼容性的前提下,更新模型以适应新数据分布。 |
| 记忆更新 | 动态调整记忆缓冲区,存储代表性样本以适应未来的模型更新。 |
总结
论文通过 L2R 的架构和流程,系统性地解决了动态数据环境中的分布漂移和效率问题。其核心在于:
- 数据选择:精确筛选支持负样本,确保训练有效性。
- 向后兼容性:通过排名对齐目标实现新旧数据的无缝衔接。
- 记忆更新:通过动态记忆机制,平衡新知识学习和旧知识保留。
这些模块协同工作,使 L2R 方法在效果和效率之间实现了良好的平衡,适用于现实中的检索场景。
问题一 文章是如何描述和处理 数据分布漂移的
以下是论文对 数据分布漂移(Data Distribution Drift)在第一阶段检索中的描述、产生原因、影响以及解决方案的详细分析:
数据分布漂移的描述
数据分布漂移指的是在真实应用场景中,随着时间推移,数据的特征分布发生变化。例如,新的文档和查询不断涌现,这些新增数据的分布可能与先前的数据显著不同。
在第一阶段检索任务中,分布漂移表现为:
- 文档分布的动态变化:新事件(如 ChatGPT 的发布)可能引发大量相关文档涌现,这些文档的内容分布与旧文档有显著差异。
- 查询需求的演变:用户的检索需求随着新的趋势或事件发生变化,新的查询可能与历史数据不匹配。
数据分布漂移的产生原因
- 文档新增:真实世界中的数据源(如互联网)不断产生新内容。
- 分布不均:新文档可能集中在特定主题(如突发热点事件),导致局部领域的分布发生剧烈变化。
- 标注不足:新文档通常未经过标注(即缺乏相关性标签),进一步增加了处理复杂性。
数据分布漂移的影响
- 模型泛化性能下降
- 使用旧数据训练的检索模型难以适应新分布的数据。
- 导致模型对新文档和新查询的检索效果不佳。
- 高代价的重建索引
- 每次模型更新后,需要重新计算所有旧文档的嵌入,并重建索引,这在大规模文档集合中成本极高。
- 遗忘旧知识
- 模型在学习新数据时可能遗忘旧数据中的知识,导致对历史查询的检索效果下降。
解决数据分布漂移的思路
论文提出了一种面向第一阶段检索的持续学习方法(L2R),从以下几个方面解决数据分布漂移的问题:
1. 数据选择策略
论文设计了两种策略,以适应新分布并平衡新旧数据的学习:
- 新数据选择
- 筛选新的支持负样本,避免将潜在的未标注正样本误作为负样本。
- 提高样本的多样性,减少冗余。
- 记忆数据选择
- 从记忆缓冲区中挑选与新样本不同的历史样本,用于模型更新,以防止遗忘旧知识。
2. 排名对齐目标
为减少分布漂移的影响,论文引入了 排名对齐目标:
- 兼容性学习:通过排名对齐目标,确保新模型在生成新文档嵌入时,与旧文档嵌入兼容,从而避免频繁重建索引。
- 双向监督
- 老模型对旧数据排名的监督,有助于新模型继承旧知识。
- 新模型对新数据排名的优化,有助于学习新知识。
3. 记忆机制
L2R 使用记忆机制缓解分布漂移的影响:
- 存储代表性样本:在记忆缓冲区中存储过去重要的负样本,以防止遗忘旧知识。
- 动态更新:根据新数据分布动态调整记忆样本,平衡旧知识保留与新知识学习。
解决方案的有效性
通过构建 LL-LoTTE 和 LL-MultiCPR 基准数据集,论文对 L2R 的性能进行了验证,结果表明:
- 在严重分布漂移(如科学领域文档激增)的情况下,L2R 能显著优于传统方法(如 MIR 和 GSS)。
- 排名对齐目标不仅减少了分布漂移对模型更新的影响,还提升了检索性能。
总结
论文通过对数据分布漂移问题的详细分析,从数据选择、排序对齐、记忆机制等多个角度提出了解决方案。L2R 方法在有效适应新数据分布的同时,避免了旧知识的遗忘,并显著降低了索引重建成本。
问题二 论文关于 Backward-compatible(向后兼容性) 在第一阶段检索中的描述、目的、设置和解决方案的详细分析
以下是论文关于 Backward-compatible(向后兼容性) 在第一阶段检索中的描述、目的、设置和解决方案的详细分析:
向后兼容性的描述
在动态环境下,文档和数据不断更新,新的模型会对新数据进行学习并生成新的嵌入(embedding)。然而,传统方法需要重新计算旧文档的嵌入并重建整个索引,这会导致高昂的计算开销。为了避免这种成本,向后兼容性的目标是:
- 确保旧文档的嵌入与新模型生成的嵌入在同一个向量空间中兼容。
- 新模型无需修改旧文档的嵌入,仅需对新增文档计算嵌入,从而高效地更新索引。
向后兼容性的目的
- 减少计算成本
- 避免对大规模旧文档集合的嵌入进行重复计算,显著降低时间和资源开销。
- 提升系统效率
- 实现索引的快速更新,使系统能够实时处理新增数据。
- 保持检索性能
- 在适应新数据分布的同时,确保对旧数据的检索质量不受影响。
- 应对真实场景需求
- 真实的第一阶段检索任务需要频繁更新文档集合,向后兼容性是一种实用性很强的解决方案。
向后兼容性的基本设置
- 目标
- 实现一个更新后的模型 $ f_t$,在生成新数据嵌入时,与旧数据嵌入保持兼容性,避免重新计算 $D_{0:t-1}$(历史文档集合)的嵌入。
- 假设
- 初始文档集合 $D_0$ 的嵌入由初始模型 $f_0 $ 生成。随后的每个训练会话中,新的文档集合 $D_t$ 到达时,模型需要更新以适应新数据分布。
- 挑战
- 新模型需要在不牺牲新数据检索性能的情况下,维持对旧数据嵌入的兼容性。
论文中的解决方案
论文提出了一种基于 排名对齐目标(Ranking Alignment Objective) 的方法,以实现向后兼容性,同时避免传统方法中的效率和性能损失。具体包括以下三个核心思路:
1. 基础兼容性学习方法
使用 固定旧文档嵌入 的方法进行优化:
思路:通过固定旧文档嵌入,仅优化新文档嵌入和查询嵌入,使新模型能够在同一向量空间中工作。
方法
定义一个基本的兼容性对齐目标 $L_{\text{rank}}$,确保新模型生成的嵌入与旧模型生成的嵌入保持一致。
公式
\[\begin{aligned} L_t^{rank} &= -\log \frac{\exp(<E^q_t(q), \mathbf{d}^+_q>)}{Z} \\ where &Z=\sum_{d \in\left\{d_q^{+}\right\} \cup D_q^{\text {mem }}} \exp \left(\left\langle\mathrm{E}_t^q(q), \boldsymbol{d}\right\rangle\right)+\sum_{d \in D_q^{\text {new }}} \exp \left(f_t(q, d)\right) \end{aligned}\]问题
- 简单地固定旧嵌入可能导致新模型过度约束,难以有效学习新数据分布,从而影响新数据的检索性能。
2. 嵌入对齐目标(Embedding Alignment Objective)
对旧文档嵌入和新模型生成的嵌入进行点对点对齐:
方法:通过最小化旧文档嵌入和新模型生成嵌入的欧几里得距离,实现向后兼容性。
公式:
\[L^_{t} = \sum_{d \in\left\{d_q^{+}\right\} \cup D_q^{\text {mem}}} \frac{1}{2} \Vert E_d^t(d) - \mathbf{d}\Vert^2\]其中 $E_d^t$ 是新模型生成的嵌入,$\mathbf{d} $是旧文档的固定嵌入。
优点
- 能够维持嵌入的一致性。
缺点
- 对新模型施加过多约束,可能抑制其对新数据的学习能力。
3. 排名对齐目标(Ranking Alignment Objective)
引入更松散的列表级对齐目标,通过对排序结果进行对齐,增强新模型的灵活性:
思路
- 旧模型生成的排名信息包含了大量上下文关系,可作为对新模型的有益监督。
- 新模型在学习新数据分布时,不需要严格保持点对点一致,而是关注文档排序的整体一致性。
公式
\[\begin{equation} \begin{aligned} L^_t &= \text{KL}\left(p(D\vert q) \vert p'(D|q)\right) \\ &\text { where } D=\left\{d_q^{+}\right\} \cup D_q^{\text {mem }} \cup D_q^{\text {new }} \text {, and }\\ &\begin{aligned} & p(d \mid q)=\left\{\begin{array}{ll} \frac{\exp \left(f_t(q, d)\right)}{Z} & \text { if } d \in D_q^{\text {new }} \\ \frac{\exp \left(\left\langle\mathrm{E}_t^q(q), d\right\rangle\right)}{Z} & \text { if } d \in\left\{d_q^{+}\right\} \cup D_q^{\text {mem }} \end{array},\right. \\ & p^{\prime}(d \mid q)=\frac{\exp \left(f_t(q, d)\right)}{\sum_{d \in D} \exp \left(f_t(q, d)\right)} \end{aligned} \end{aligned} \end{equation}\]其中:
- $p(D \vert q)$:旧模型生成的排序分布。
- $p’(D \vert q)$:新模型基于当前嵌入生成的排序分布。
优点
- 允许新模型更灵活地探索新数据,同时保留旧数据的排序信息。
- 通过对排名的双向监督,实现新旧知识的平衡。
文中所用整体损失函数
\[\begin{aligned} L_t^{\text{com}}=L_t^{\text {rank}}+\lambda \cdot L_t^{\text{align}},\\ \text{where} L_t^{\text{align} } \text{is either} L_t^ \text{or } L_t^ \end{aligned}\]实验验证与效果
- 性能
- 排名对齐目标(Ranking Alignment Objective)显著优于嵌入对齐目标,在召回率(Recall)和平均倒数排名(MRR)等指标上表现突出。
- 效率
- 向后兼容性机制节省了 79%-81% 的嵌入计算成本。
- 灵活性
- 排名对齐目标能够在新数据的学习和旧数据的兼容性之间实现平衡,避免了简单嵌入对齐导致的性能下降。
总结
论文通过结合基础兼容性学习、嵌入对齐目标和排名对齐目标,提出了一种高效的向后兼容性解决方案。在第一阶段检索中,这种方法有效减少了重建索引的开销,同时保持了高水平的检索性能,具有重要的实际应用价值。
个人理解
一 文中提到的指标和设置
文中提到了两个指标,在这两个指标之前先定义了一个投影向量的概念。
$\mathbf{d}_{∥}$:文档 $d$ 在查询 $q$上的投影,表示 $d$ 中与 $q$ 相关的部分,计算公式为:
\[\mathbf{d}_{\parallel} = \frac{(d \cdot q)* q}{\Vert q \Vert^2}\]
这就是将文档向量$d$ 根据是否与 $q$ 方向一致进行了分解。
1. Positive Sample Superiority (PSS)
设计目的
PSS 用于评估某个文档是否为“支持负样本”(support negatives),即模型可以利用该文档有效学习决策边界。具体来说,PSS 衡量的是给定查询 $q$,文档 $d$ 相较于正样本 $d^+_q$ 的相关性差异。
公式
\[PSS(d, d^+_q; q) = \text{sign}(\mathbf{d}^+_{\parallel q} - \mathbf{d}_{\parallel q}) \cdot \Vert \mathbf{d}^+_{\parallel q} - \mathbf{d}_{\parallel q} \Vert_2\]- $d$:候选文档的嵌入向量。
- $d^+_q$:查询 $q$ 的正相关文档的嵌入向量。
- $q$:查询的嵌入向量。
- $\mathbf{d}_{∥}$:文档 $d$ 在查询 $q$上的投影,表示 $d$ 中与 $q$ 相关的部分
- $\mathbf{d}_{\parallel}^{+}$:正样本$d^+_q$ 的投影,在查询 $q$上的投影。
- $\text{sign}$ 函数:如果 $\mathbf{d}^+{\parallel q} - \mathbf{d}{\parallel q}$ 和 $\mathbf{d}^+_{\parallel q}$方向相同,则为 $+1$;否则为 $-1$。
- $|\cdot|_2$:欧几里得范数,用于计算向量之间的距离。
是已有一个 查询 $q$ 和另一个正相关文档 $d^+_q$ ,然后 计算另一个文档 $d$ 相较于正样本 $d^+_q$ 的差异。
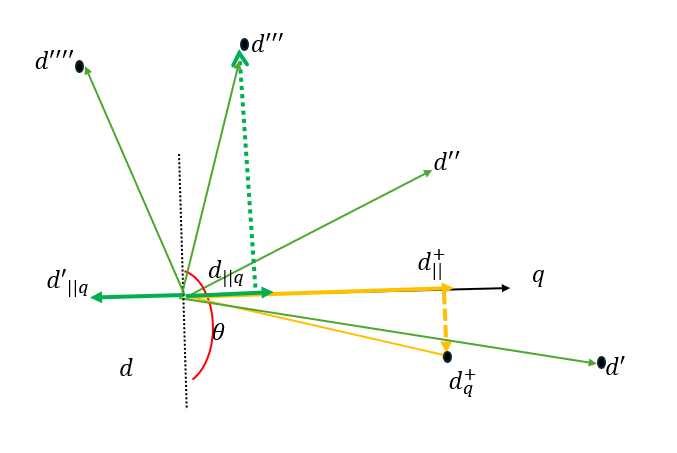
PSS 衡量候选文档 $d$ 与查询 $q$ 的相关性是否显著低于正样本$d^+_q$。
如果符号是正,即 $\mathbf{d}^+{\parallel q} - \mathbf{d}{\parallel q}$ 大于0,说明候选文档 $d$ 在 $q$ 上的投影 $\mathbf{d}{\parallel q}$ 在 $\mathbf{d}^+{\parallel q}$ 的($q$方向的负)左侧,代表与 $\mathbf{d}^+_{\parallel q}$ 没有那么相关的数据
如果符号是负,即 $\mathbf{d}^+{\parallel q} - \mathbf{d}{\parallel q}$ 小于0, 说明候选文档 $d$ 在 $q$上的投影 $\mathbf{d}{\parallel q}$ 在 $\mathbf{d}^+{\parallel q}$ 的右( $q$ 方向的正侧)侧,选文档 $d$ 和正样本文档 $\mathbf{d}_{\parallel}^{+}$ 在 查询 $q$ 上的投影方向是一致的
如果数值越大,说明候选文档 $d$ 和正样本文档 $\mathbf{d}_{\parallel}^{+}$ 的距离越远
最终如果是正的数值越大,说明与正样本越不相关
2. Inter Sample Diversity (ISD)
设计目的
ISD 用于评估候选文档 $d$ 相较于文档集合 $D$ 的多样性。目的是在负样本选择中减少冗余,确保被选择的样本信息具有多样性。
公式
\[ISD(d, D; q) = \frac{1}{|D|} \sum_{d' \in D} \|\mathbf{d}_\perp - \mathbf{d}'_\perp\|_2\]公式符号含义
- $d$:当前候选文档的嵌入向量。
- $D$:当前文档集合。
- $q$:查询的嵌入向量。
- $\mathbf{d}_\perp$:文档 $d$ 嵌入向量中与查询$ q$ 无关的部分
- $\mathbf{d}’_{\perp}$:集合 $D$ 中文档 $d^′$的无关部分。
- $∣D∣$:集合 $D$ 的文档数量。
含义与作用
- ISD 衡量文档 d 与集合 D 中其他文档在无关信息上的多样性。
- 较高的 ISD值表明 $d$ 的信息与集合 D中其他文档 $d’$ 不重复,有助于构建更丰富的样本集。
- ISD 减少了选择负样本时的冗余,提高模型训练的效率和效果。
这两个指标的设计通过:
- PSS 确保所选负样本有效,避免正样本被错误选中。
- ISD 提高样本集的多样性,覆盖更多的决策边界。
思考,这第二个设计是不是有问题,这只体现了 $\mathbf{d}_\perp$的多样性,
文档信息
- 本文作者:zuti666
- 本文链接:https://zuti666.github.io/2024/11/30/Paper-Reading-Note-9-First-stage-Retrieval-L2R/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)