理解 二阶曲率一
我们考虑模型在近似最小值的局部的二阶曲率问题。
首先,我们给出基本的设定
符号约定- 学习目标与模型
假设我们想要学习数据$x$与$y$的一个关系$f$, 我们假定这些数据是来自于一个统一的分布$\mathcal{D}$,所以其内部存在一定的相似性或者联系,这样我们才能根据学习到的$f$ ,对于新的来自同一分布的类似数据$\bar{x}$ 做出相关预测,并且我们能够相信这个预测的结果是可靠的。
并且我们希望模型是一个鲁棒的结果,也就是说对于$\bar{x}+\epsilon$ ,其中$\epsilon$ 是一些噪声,也能得到一个可靠的预测结果。
更进一步,我们认为所学习的关系$f$是一个普遍规律,希望模型具有更加强大的泛化能力,即当遇到一个类似的分布$\mathcal{D}_1$, 我们所学习到的关系$f$依旧能够起到作用。
数据分布 与 损失函数
首先,我们对数据分布做出假设 , 数据是来自于同一分布,或者使用更加准确的话说,假设我们训练使用的每一个样本都是独立的从同一个分布中采样得来的,即 $(x,y)\overset{\text{i.i.d.}}{\sim} \mathcal{D}$ 。
但实际上,我们不能获取这个数据分布完整的数据,只能通过采样尽可能获得更多的数据,也就是我们进行训练模型所使用的数据集。当我们使用数据集的时候,会划分为训练集和测试集,使用训练集训练模型,使用测试集测试我们模型的训练效果。并且有时候还会在训练集中划分一部分作为验证集,目的是在训练过程中来验证模型的能力的变化。我们也假设所使用的训练集和测试集的样本都是来自于同一分布,即$S,T \overset{\text{i.i.d.}}{\sim} \mathcal{D}$。
所以实际上,我们是希望模型在整个数据分布上$D$能够学的数据的一个内在关系$f$, 但我们实际上只能得到一个有限的训练集上$S$的一个关系$\hat{f}$。 但是由于我们假设训练集的数据分布和真实的数据分布是一致的,所以我们认为我们实际训练得到的模型是学到了整个数据分布的内在关系。
在训练的时候,我们根据这个关系在数据上的表现,定义一个损失函数进行刻画。 我们的理想的损失函数是刻画了这个关系在真实分布上的表现。 \(\begin{align}\label{eq: expected risk} L_{\mathcal{D}}(f) &:= \mathbb{E}_{(x, y) \sim \mathcal{D}}[\ell(f, x, y)]\\ &:= \mathbb{E}_{S \overset{\text{i.i.d.}}{\sim} \mathcal{D}} \hat{L}_{S}(f)=\mathbb{E}_{S \overset{\text{i.i.d.}}{\sim} \mathcal{D}} \ [\frac{1}{n}\sum_{i=1}^{n=|S|}\ell(f, x_i, y_i)] \end{align}\) 但是由于数据的限制,我们只能获得在训练集上的损失。而我们在训练集上进行训练的目的就是得到一个在训练集上表现好的模型,同时这个模型也被认为是在整个数据分布上表现足够好。
\[\begin{equation} \hat{f} := \arg\min_{f \in \mathcal{F}} \hat{L}_S(f) \quad \text{such that} \quad L_{\mathcal{D}}(\hat{f}) \text{ is also small} \end{equation}\]实际上模型在测试集的表现和真实分布下的表现是有差异的,我们需要刻画两者损失的具体区别,一般我们有以下的关系
\[\begin{equation} L_{\mathcal{D}}(f) \leq \hat{L}_S(f) + \text{complexity penalty} \end{equation}\]根据上面的表述,我们就可以在训练集上训练模型的时候主动将这个差距考虑进去,也就是
\[\begin{equation} \hat{f} := \arg\min_{f \in \mathcal{F}} \left[ \hat{L}_S(f) + \text{complexity penalty} \right] \end{equation}\]这个复杂项会惩罚项怎么添加,就依赖于人们对数据分布的差异的理解了。
模型
我们考虑一个在图像识别任务下的典型的神经网络模型$M$,其内部包含了若干层,一般来说可以将其划分为三个部分,输入层,中间层,输出层,或者按着功能划分分为两部分,特征提取层和分类层。
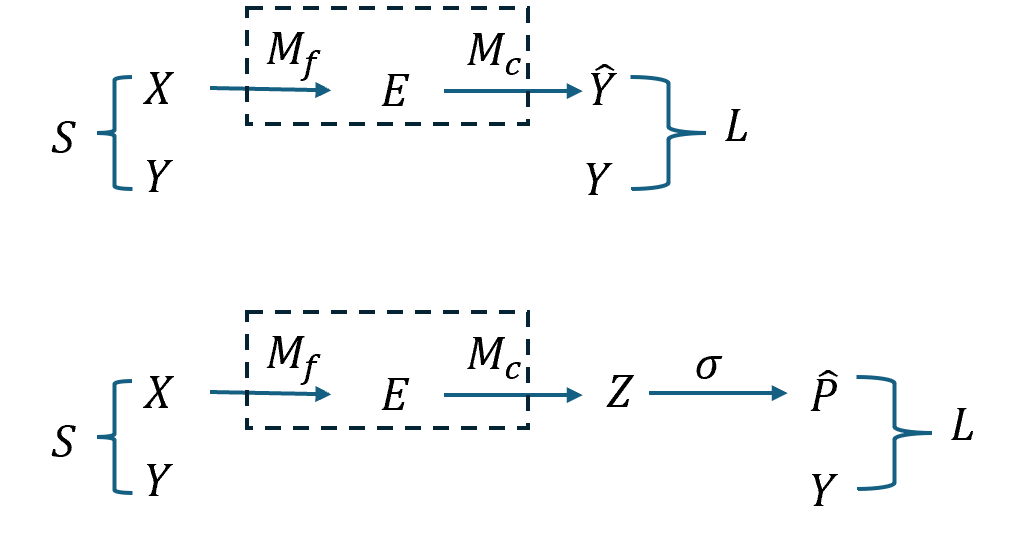
上图中第二个和第一个的区别在于,对于模型的输出最后使用softmax函数进行了归一化,使其满足概率的要求,将原来的输出映射到概率空间。此时对应的 $y$ 是一个one-hot 编码,也可以被认为是一个概率,所以这里损失函数衡量的就是在概率空间下模型的输出和真实标签的距离。可以使用交叉熵损失或者KL divergence 来进行衡量模型的预测概率 $p$ 和真实分布 $y$ 的差异。
这里提到的softmax函数作用如下,输入为$z=[z_1,\cdots,z_n]^T$,输出为概率分布 $p=[p_1,\cdots,p_n]^T$ 这里的 $n$ 是预测的类别 $C$,所以有\(z,p\in\mathbb{R}^{C}\)
\[p_i=\frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}}\]其求导结果为一个雅克比矩阵如下
\[\frac{\partial p_i}{\partial z_j}=p_i(\mathbf{1}_{i=j}-p_j)\\ \frac{\partial p}{\partial z}= J_{sm}(z)= \text{diag}(p)-pp^T \in\mathbb{R}^{C\times C} \\ =\left[\begin{array}{cccc} p_1\left(1-p_1\right) & -p_1 p_2 & \cdots & -p_1 p_n \\ -p_2 p_1 & p_2\left(1-p_2\right) & \cdots & -p_2 p_n \\ \vdots & \vdots & \ddots & \vdots \\ -p_n p_1 & -p_n p_2 & \cdots & p_n\left(1-p_n\right) \end{array}\right]\]
具体的分类过程如下,其中黄色是特征$e$,W表示最后一个线性分类层,对于得到的分类结果称为 logits, 其维度和概率输出的维度一致(就是需要被预测的类别),但是没有使用softmax进行概率归一化。然后经过概率归一化得到概率的输出。
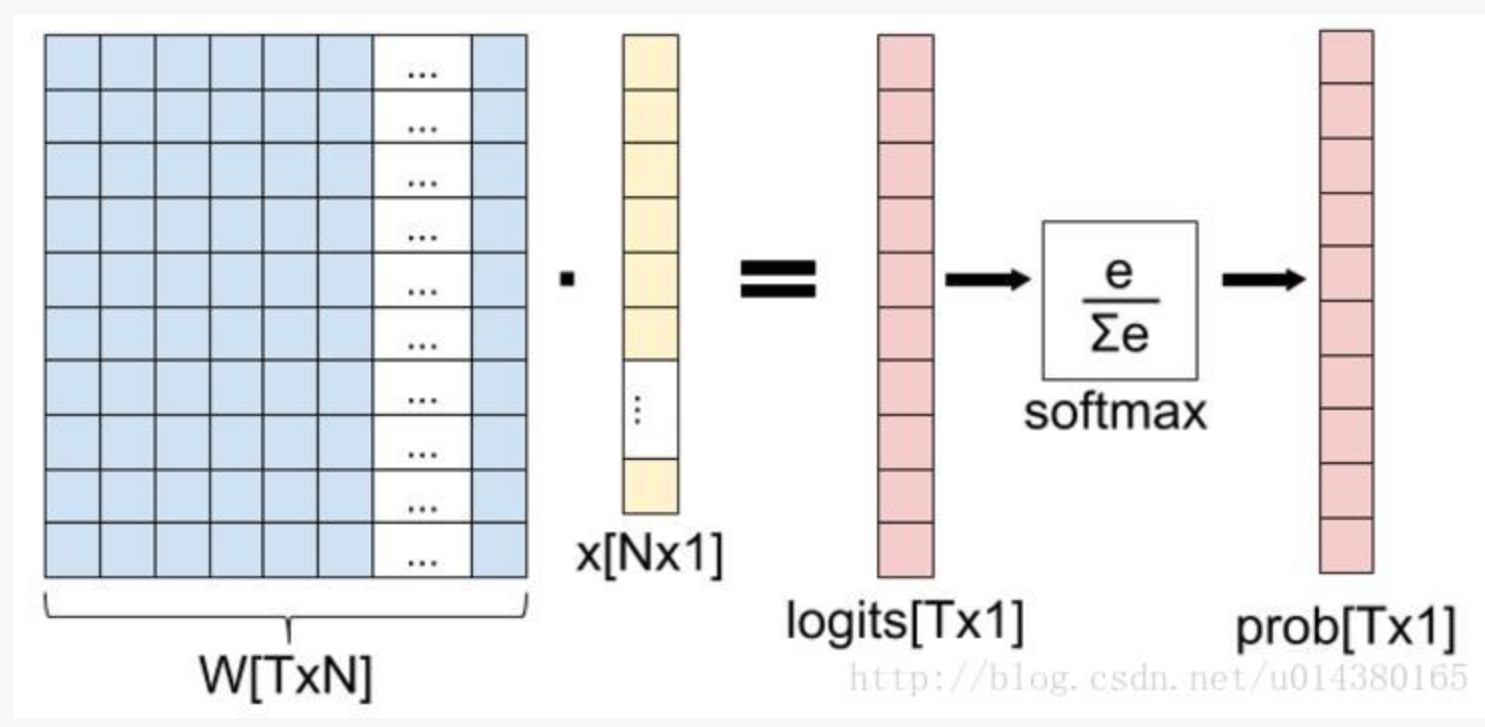
如果去掉softmax函数,即第一个图,那么也可以直接使用欧氏距离来衡量模型输出和真实标签的差距 $|y-\hat{y}|$ 。 这里就不是在概率空间进行思考,而是将模型的输出或者特征作为一个高维空间向量,使用欧氏距离来进行刻画两个向量的差异。在高维向量空间下,另外还有一种常见的就是余弦距离,用来衡量两个向量方向的相似而不是距离的差异。两个向量夹角越小,趋于0度,余弦值接近于1,方向更加吻合。
链式法则
在模型的训练过程中,使用链式法则进行反向传递梯度更新神经网络,
记模型 $f$ 的全部参数为 $\theta$ , 我们上面讨论的model也就可以表示为 $M=f(\theta)$。对于单个样本 $i$ 来说,损失函数$\ell_i=\ell(f(x_i;\theta),y_i)$ ,对于一个批次的样本 $x=[x_1,\cdots,x_i,\cdots,x_b]^T$, 其损失函数为$L(f(x;\theta),y)=\frac{1}{b} \sum_{i=1}^b\ell(f(x_i;\theta),y_i)$。
梯度更新过程为
\[\frac{\partial L}{\partial \theta}\]更进一步,我们基于上面的模型分解,将模型分为了特征提取器$M_f$和线性分类层$M_c$,对应参数可以分别记作 $\theta_f$ 和 $\theta_c$ 。由于线性分类层只有一层且其作用是线性的,可以直接表示为$f(e;\theta_c)=W_c \cdot e$。
然后基于上述两种分解方式,我们分别给出对应的梯度的链式法则
对于第一种 , 损失函数为 $ L(\hat{y},y)$ , 经过分解的模型处理过程为
\[e = f(x;\theta_f), \hat{y}=W_c e\]为了清晰起见,$e\in\mathbb{R}^d$,$W_c\in\mathbb{R}^{C\times d}$,$z\in\mathbb{R}^C$,$p\in\mathbb{R}^C$。
合并在一起可以表示为
\[\hat{y}=f(f(x;\theta_f);\theta_c)= W_c f(x;\theta_f)\],对应的损失函数可以表示为 $L(W_c \cdot f(x;\theta_f),y)$。
接下来我们分别给出对线性分类层和特征提取层的链式求导
损失函数对输入求导如下
\[\frac{\partial L}{\partial e} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial e } = W_c^T \frac{\partial L}{\partial \hat{y}}\\ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial e} \frac{\partial e}{\partial x}= (\frac{\partial e}{\partial{x}})^T (W_c^T \frac{\partial L}{\partial \hat{y}} )\\\]在梯度更新过程中,损失函数分别对线性分类层权重和特征提取层权重求导如下
\[\frac{\partial L}{\partial W_c} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial W_c } = \frac{\partial L}{\partial \hat{y}} e^T \\ \frac{\partial L}{\partial \theta_f} = \frac{\partial L}{\partial e} \frac{\partial e}{\partial \theta_f}= (\frac{\partial L}{\partial \hat{y}} W_c) \frac{\partial e}{\partial{\theta_f}} \\\]由于一般来说特征提取层是包含不同架构的多层线性网络看,这里就不具体展开后面的推导,在pytorch中这里是代码可以依据计算图根据链式法则实现这个$\frac{\partial e}{\partial{\theta_f}}$过程
对于第二种 , 损失函数为 $ L(\hat{p},y)$ , 经过分解的模型处理过程为
\[e = f(x;\theta_f), z=f(e;\theta_c)=W_c e,p=\text{softmax} (z)\]合并在一起可以表示为
\[\hat{p}= \text{softmax}(f(f(x;\theta_f);\theta_c))= \text{softmax}(W_c \cdot f(x;\theta_f))\]对应的损失函数可以表示为 $L=L(p,y)=L(\text{softmax}(W_c \cdot f(x;\theta_f)),y)$。
接下来我们分别给出对线性分类层和特征提取层的链式求导
根据上面我们知道
\[\frac{\partial p}{\partial z}= J_{sm}(z)= \text{diag}(p)-pp^T\]
损失函数对输入求导如下
\[\frac{\partial L}{\partial z} = \frac{\partial L}{\partial \hat{p}} \frac{\partial \hat{p}}{\partial z } = J_{sm}(z) \frac{\partial L}{\partial \hat{p}} \\ \frac{\partial L}{\partial e} = \frac{\partial L}{\partial \hat{p}} \frac{\partial \hat{p}}{\partial z } \frac{\partial z}{\partial e } =W_c^T J_{sm}(z) \frac{\partial L}{\partial \hat{p}}\\ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial \hat{p}} \frac{\partial \hat{p}}{\partial z } \frac{\partial z}{\partial e } \frac{\partial e}{\partial x}= {\frac{\partial e}{\partial{x}}}^T (W_c^T J_{sm}(z) \frac{\partial L}{\partial \hat{p}} ) \\\]损失函数对分别对线性分类层权重和特征提取层权重求导如下
$$ \frac{\partial L}{\partial W_c} = \frac{\partial L}{\partial \hat{p}} \frac{\partial \hat{p}}{\partial z } \frac{\partial z}{\partial W_c }= J_{sm}(z) \frac{\partial L}{\partial \hat{p}} e^T \
\frac{\partial L}{\partial \theta_f} = \frac{\partial L}{\partial \hat{p}} \frac{\partial \hat{p}}{\partial z } \frac{\partial z}{\partial e } \frac{\partial e}{\partial{\theta_f}}=\Big(\frac{\partial e}{\partial \theta_f}\Big)^{!\top} W_c^{\top} J_{\rm sm}(z) \frac{\partial L}{\partial \hat{p}}
$$