理解 二阶曲率二 KL损失与CE损失
在基于上一节的表述后,我们考虑在带有softmax输出的分类问题中,考虑两个具体的损失函数并给出其链式求导法则,接着从定义上讨论两者的区别。
模型如下
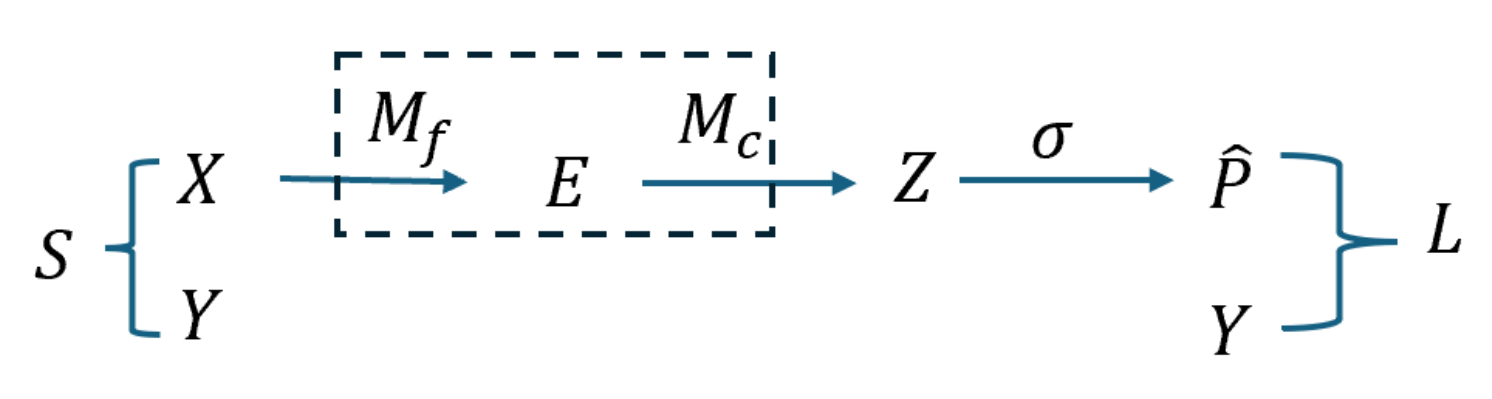
其中softmax及其导数如下
输入为$z=[z_1,\cdots,z_n]^T$,输出为概率分布 $p=[p_1,\cdots,p_n]^T$ 这里的 $n$ 是预测的类别 $C$,所以有\(z,p\in\mathbb{R}^{C}\) 。softmax函数表达式如下
\[p_i=\frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}}\]其求导结果为一个雅克比矩阵如下
\[\frac{\partial p_i}{\partial z_j}=p_i(\mathbf{1}_{i=j}-p_j)\\ \frac{\partial p}{\partial z}= J_{sm}(z)= \text{diag}(p)-pp^T \in\mathbb{R}^{C\times C} \\ =\left[\begin{array}{cccc} p_1\left(1-p_1\right) & -p_1 p_2 & \cdots & -p_1 p_n \\ -p_2 p_1 & p_2\left(1-p_2\right) & \cdots & -p_2 p_n \\ \vdots & \vdots & \ddots & \vdots \\ -p_n p_1 & -p_n p_2 & \cdots & p_n\left(1-p_n\right) \end{array}\right]\]
交叉熵损失
公式与含义推导
我们将KL散度公式进行变形 :
\[\begin{aligned} KL(p||q) &= \sum_{i=1}^n p(x_i) \cdot log(\frac{p(x_i)}{q(x_i)}) \\ &= \sum_{i=1}^n p(x_i) \cdot log\ p(x_i) - \sum_{i=1}^n p(x_i) \cdot log\ q(x_i)\\ &= -H(p(x)) + [ \sum_{i=1}^n p(x_i) \cdot - log\ q(x_i)] \end{aligned}\]等式的前一部分恰巧就是真实分布$P$的信息熵,为恒定值。等式的后一部分,就是交叉熵
\[H(p,q) =- \sum_{i=1}^n p(x_i) \cdot log\ q(x_i)\]$n$表示分布定义的随机变量的所有可能的取值。在机器学习中,一般p表示真实分布,而q表示预测分布
链式求导
交叉熵:
\[L(y,p)=-\sum_{k=1}^{C} y_k \log p_k\],其中 $y$ 可为 one-hot 或软标签分布($\sum_k y_k=1$)。
Softmax 雅可比:$J_{\rm sm}(z)=\mathrm{diag}(p)-pp^{\top}$(对称)。
基本恒等式:,从而
\[\displaystyle \frac{\partial L}{\partial p}=-\,y\oslash p\text{(逐元素除)}\\ \frac{\partial L}{\partial z}=J_{\mathrm{sm}}(z) \frac{\partial L}{\partial p}=p-y .\]进一步我们有, 对于单样本,我们有
对于输入的梯度
\[\begin{aligned} \frac{\partial L}{\partial z} &= p-y,\\[4pt] \frac{\partial L}{\partial e} &= \Big(\frac{\partial z}{\partial e}\Big)^{\!\top}\frac{\partial L}{\partial z} = W_c^{\top}(p-y),\\[6pt] \frac{\partial L}{\partial x} &= \Big(\frac{\partial e}{\partial x}\Big)^{\!\top}\frac{\partial L}{\partial e} = \Big(\frac{\partial e}{\partial x}\Big)^{\!\top} W_c^{\top}(p-y). \end{aligned}\]对于权重更新的梯度
\[\frac{\partial L}{\partial W_c} &= \Big(\frac{\partial z}{\partial W_c}\Big)^{\!\top}\frac{\partial L}{\partial z} = (p-y)\,e^{\top}\quad(\text{形状 }C\times d),\\[6pt] \frac{\partial L}{\partial \theta_f} &= \Big(\frac{\partial e}{\partial \theta_f}\Big)^{\!\top}\frac{\partial L}{\partial e} = \Big(\frac{\partial e}{\partial \theta_f}\Big)^{\!\top} W_c^{\top}(p-y),\\[6pt]\]KL散度损失
KL 散度衡量两个概率分布 P 和 Q 之间的距离(严格来说是“相对熵”,不是对称的距离),其定义如下:
\[\begin{aligned} & \boldsymbol{D}_{\boldsymbol{K} \boldsymbol{L}}(\boldsymbol{P} \| \boldsymbol{Q}) \\ & :=\sum_{i=\mathbf{1}}^m p_i \cdot\left(f_Q\left(q_i\right)-f_P\left(p_i\right)\right) \\ & =\sum_{i=1}^m p_i \cdot\left(\left(-\log _2 q_i\right)-\left(-\log _2 p_i\right)\right) \\ & =\sum_{i=1}^n p(x_i) \cdot log\frac{p(x_i)}{q(x_i)} \end{aligned}\]在KL中是有方向的,也就是说$\boldsymbol{D}{\boldsymbol{K} \boldsymbol{L}}(\boldsymbol{P} | \boldsymbol{Q})$ 和 $\boldsymbol{D}{\boldsymbol{K} \boldsymbol{L}}(\boldsymbol{ Q} | \boldsymbol{P})$ 并不是等价的。P 在前,就表示以P为基准,去考虑P和Q相差有多少。KL 散度 $\boldsymbol{D}_{\boldsymbol{K} \boldsymbol{L}}(\boldsymbol{P} | \boldsymbol{Q})$ 反映了用 Q 去近似 P 时造成的信息损失。
在监督学习分类中,更常见且清晰的对应是:$P$ 为目标/真实分布(经验标签分布 $y$),$Q$ 为模型的预测分布 $p$。让 $Q$ 近似 $P$;梯度只惩罚 $Q(x)=0$ 而 $P(x)>0$ 的地方(会变成无穷大),因此 $Q$ 倾向覆盖 $P$ 的所有支撑(“mode-covering/零回避 zero-avoiding”)。 监督分类里取 $P=y$、$Q=\hat p$,最小化 $D_{KL}(y|\hat p)$ 就是最小化交叉熵,
在标准 VAE 中,先验 p(z) 通常固定,因此 KL(q ∥ p) 的梯度主要更新 q 的参数,使 q 靠近 p。”
在机器学习中,常见的表述为
\[L=\boldsymbol{D}_{\boldsymbol{K} \boldsymbol{L}}(y\|\hat{p})=\sum_{k} y_k \log\frac{y_k}{\hat{p}_k}\]该损失与交叉熵仅差一个与参数无关的常数($\sum y_k\log y_k$),因此梯度与交叉熵完全相同