二阶曲率4 二阶泰勒展开 logit空间 - 概率空间 - 损失函数
(参数扰动 → logit → 概率/损失;再到 Hessian / GGN / Fisher 的统一)
0. 全局图景(先把地图挂起来)
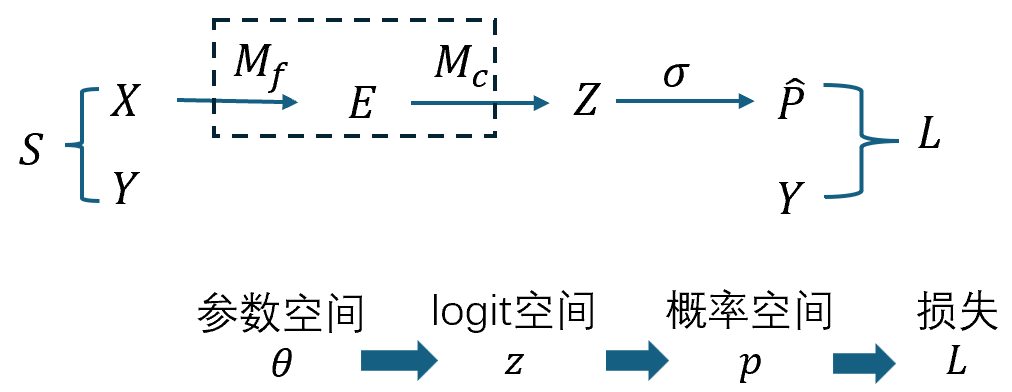
我们将围绕二阶泰勒展开把上面四层接成一条可计算的链,并在“二阶项”处对比 Hessian / GGN / Fisher。
1. 记号与最小背景
$\theta\in\mathbb{R}^p$:全部模型参数;$\Delta\theta$:其小扰动。
$z(\theta)\in\mathbb{R}^C$:logits;
$J_z:=\partial z/\partial\theta\in\mathbb{R}^{C\times p}$(雅可比)。
$\mathcal H_z:={\nabla_\theta^2 z_k}_{k=1}^C$:每个 logit 的参数 Hessian 组成的张量; $\mathcal H_z[\Delta\theta,\Delta\theta]\in\mathbb{R}^C$:其对 $(\Delta\theta,\Delta\theta)$ 的双线性作用。
损失 $L(y,z)$ 对 $z$ 的一/二阶: $g_z:=\partial L/\partial z\in\mathbb{R}^{C}$,
$H_L:=\nabla_z^2 L\in\mathbb{R}^{C\times C}$。
余项控制:若 $\nabla^3 z,\nabla^2 L$ 在邻域有界,则泰勒余项为 $O(|\Delta\theta|^3)$。
2. 第一步:参数扰动 $\Rightarrow$ logit 变化(二阶泰勒)
对小步长 $\Delta\theta$:
$\boxed{z(\theta+\Delta\theta)\ \approx\ z(\theta)\ +\ J_z\,\Delta\theta\ +\ \tfrac12\,\mathcal H_z[\Delta\theta,\Delta\theta].}$
- 一阶项 $J_z\Delta\theta$:参数对 logit 的线性敏感度。
- 二阶项 $\frac12\mathcal H_z[\Delta\theta,\Delta\theta]$:模型在参数上的非线性曲率修正。
直觉:如果把网络在当前点线性化,就只剩 $J_z\Delta\theta$;保留 $\mathcal H_z$ 才能捕捉“网络本身的弯曲”。
3. 第二步:logit 变化 $\Rightarrow$ 损失变化(二阶泰勒)
损失对 $z$ 做二阶泰勒展开
$\Delta L\ \approx\ g_z^{\top}\Delta z\ +\ \tfrac12\,\Delta z^{\top}H_L\,\Delta z.$
把 $\Delta z$ 用上一步替换,并只保留总二阶(二次项里取 $\Delta z\approx J_z\Delta\theta$ 即可):
\[\Delta L\ \approx\ \underbrace{g_z^{\top}J_z\,\Delta\theta}_{\text{一阶}} +\tfrac12\underbrace{(J_z\Delta\theta)^{\top}H_L(J_z\Delta\theta)}_{\text{“损失曲率通道”}} +\tfrac12\underbrace{g_z^{\top}\mathcal H_z[\Delta\theta,\Delta\theta]}_{\text{模型自身二阶(非线性)}}\]把 $\Delta z$ 代入并逐项分解与定阶:
1) 线性项 $g_z^{\top}\Delta z$
$\begin{aligned} g_z^{\top}\Delta z &= g_z^{\top}\Big(J_z\Delta\theta+\tfrac12\,\mathcal H_z[\Delta\theta,\Delta\theta]\Big) + O(|\Delta\theta|^3)\ &=\underbrace{g_z^{\top}J_z\Delta\theta}{O(|\Delta\theta|)} \;+\;\underbrace{\tfrac12\,g_z^{\top}\mathcal H_z[\Delta\theta,\Delta\theta]}{O(|\Delta\theta|^2)} \;+\;O(|\Delta\theta|^3). \end{aligned}$
第一项是一阶($\propto |\Delta\theta|$)。
第二项是二阶($\propto |\Delta\theta|^2$)。
2) 二次项 $\tfrac12\,\Delta z^{\top} H_L\,\Delta z$
令 $a:=J_z\Delta\theta=O(|\Delta\theta|),\qquad b:=\tfrac12\,\mathcal H_z[\Delta\theta,\Delta\theta]=O(|\Delta\theta|^2),$
则 $\Delta z=a+b+O(|\Delta\theta|^3).$
用对称性($H_L^\top=H_L$)展开:
$\begin{aligned} \tfrac12\,\Delta z^{\top} H_L\,\Delta z &=\tfrac12\,(a+b)^{\top}H_L(a+b) + O(|\Delta\theta|^4)\ &=\tfrac12\,\underbrace{a^{\top}H_L a}{O(|\Delta\theta|^2)} +\underbrace{a^{\top}H_L b}{O(|\Delta\theta|^3)} +\tfrac12\,\underbrace{b^{\top}H_L b}_{O(|\Delta\theta|^4)} \;+\;O(|\Delta\theta|^4). \end{aligned}$
$a^{\top}H_L a$ 是二阶;
- 交叉项 $a^{\top}H_L b$ 是三阶(丢弃于“总二阶”近似);
- $b^{\top}H_L b$ 是四阶(同样丢弃)。
因此在“只保留总二阶”下:
$\tfrac12\,\Delta z^{\top} H_L\,\Delta z \;=\;\tfrac12\,(J_z\Delta\theta)^{\top} H_L (J_z\Delta\theta)\;+\;O(|\Delta\theta|^3).$
3) 汇总得到“只保留总二阶”的最终式
把 1) 与 2) 的保留项合并:
\[\Delta L \;\approx\; \underbrace{g_z^{\top}J_z\Delta\theta}_{\text{一阶}} \;+\;\tfrac12\,\underbrace{(J_z\Delta\theta)^{\top} H_L (J_z\Delta\theta)}_{\text{二阶(GN/Fisher 块)}} \;+\;\tfrac12\,\underbrace{g_z^{\top}\mathcal H_z[\Delta\theta,\Delta\theta]}_{\text{二阶(模型非线性)}} \;+\;O(\|\Delta\theta\|^3).\]这正是我们在正文中给出的式子;也解释了为什么在二次项里可以把 $\Delta z$ 用 $J_z\Delta\theta$ 近似:因为包含 $\mathcal H_z$ 的那一部分在二次型里只会产生三阶及以上的项(交叉项 $a^{\top}H_L b\sim O(|\Delta\theta|^3)$ 与 $b^{\top}H_L b\sim O(|\Delta\theta|^4)$),在“总二阶”近似中应当丢弃。
备注(等价的微分形式,一行见底)
用二阶复合函数微分公式也可一行得到相同结果: 对复合 $L(z(\theta))$,有
$\mathrm{d}L = g_z^{\top}\mathrm{d}z,\qquad \mathrm{d}^2L = (\mathrm{d}z)^{\top}H_L\,\mathrm{d}z + g_z^{\top}\mathrm{d}^2 z.$
沿方向 $\Delta\theta$ 代入 $\mathrm{d}z=J_z\Delta\theta$,$\mathrm{d}^2 z=\mathcal H_z[\Delta\theta,\Delta\theta]$,并取 $\Delta L \approx \mathrm{d}L+\tfrac12\,\mathrm{d}^2L$,即得
$\Delta L \approx g_z^{\top}J_z\Delta\theta +\tfrac12\,(J_z\Delta\theta)^{\top}H_L(J_z\Delta\theta) +\tfrac12\,g_z^{\top}\mathcal H_z[\Delta\theta,\Delta\theta].$
这与上面的按阶展开完全一致。
由此可读出(在 $\theta$ 处):
\[\boxed{\ \nabla_\theta L=J_z^{\top}g_z,\qquad \nabla_\theta^2 L=J_z^{\top}H_LJ_z\ +\ \mathcal T,\ \ \mathcal T_{ab}=\sum_k (g_z)_k\,\frac{\partial^2 z_k}{\partial\theta_a\partial\theta_b}.}\]- $J_z^{\top}H_LJ_z$:经由 logits 的二阶曲率通道(正半定,数值稳定)
- $\mathcal T$:网络非线性引起的二阶项(可能导致 Hessian 不定)
到这里,你已经得到了最核心的“分解版 Hessian”: $\displaystyle H\ =\ \underbrace{J_z^{\top}H_LJ_z}{\text{GGN/Fisher 块}}\ +\ \underbrace{\mathcal T}{\text{被 GGN/Fisher 忽略}}$.
4. 两个常用损失的 $H_L$(带上直觉)
4.1 Sigmoid + Bernoulli-CE(多标签/二分类)
- $p=\sigma(z)$;
- $g_z=p-y$;
- $\displaystyle H_L=\mathrm{diag}\big(p\odot(1-p)\big)$(每维最多 $1/4$)。
二阶项上界:
$\tfrac12 (J_z\Delta\theta)^{\top}H_L(J_z\Delta\theta)\le \tfrac18|J_z\Delta\theta|^2.$
4.2 Softmax + 多类-CE(多分类)
- $p=\mathrm{softmax}(z)$;
- $g_z=p-y$;
- $\displaystyle H_L=\mathrm{diag}(p)-pp^{\top}$(协方差型,$|H_L|_2\le \tfrac12$)。
这两种损失都给出PSD 的 $H_L$,因此 $J_z^{\top}H_LJ_z$ 也 PSD —— 这就是 GGN/Fisher 稳定的根源。
5. GGN、Fisher、Hessian:定义—联系—差别
5.1 GGN(Generalized Gauss–Newton)
定义(对样本/批次取均值):
$\boxed{G\ :=\ \mathbb E[J_z^{\top}H_LJ_z].}$
含义:把网络在二次项里线性化(只留 $J_z\Delta\theta$),因此等价于 Hessian 去掉 $\mathcal T$。 性质:正半定(PSD)、数值稳健、易做矩阵–向量乘(MvP)。
5.2 Fisher(分布空间的局部度量)
| 监督学习用条件模型 $p_\theta(y | x)$, |
Fisher:
| $F=\mathbb E_{x}\ \mathbb E_{y\sim p_\theta(\cdot | x)} \big[\nabla_\theta\log p_\theta(y | x)\nabla_\theta\log p_\theta(y | x)^{\top}\big].$ |
链式换元到 $z$-空间:
| $\boxed{F=\mathbb E_x\big[J_z^{\top}\,F_R(z)\,J_z\big]},\quad F_R(z)=\mathbb E_{y\sim r(\cdot | z)}![\nabla_z\log r\,\nabla_z\log r^{\top}].$ |
5.3 Fisher ≡ GGN 的条件(为什么二者常相等)
| 若损失是负对数似然 $L(y,z)=-\log r(y | z)$,且 $r$ 属指数族且 $z$ 为自然参数(如 Sigmoid/Bernoulli-CE、Softmax/Multinomial-CE、固定方差高斯/MSE),则 |
$\boxed{F_R(z)=H_L(z)}\ \Rightarrow\ \boxed{F=\mathbb E[J_z^{\top}H_LJ_z]\ \equiv\ G.}$
结论:在最常见的分类/回归任务下,Fisher 与 GGN 完全一致;二者都是“损失曲率通道”的参数空间表达。
5.4 与 Hessian 的关系(一句话版)
$\boxed{H\ =\ G\ +\ \mathcal T}$
- $H$:最精确,但因 $\mathcal T$ 可能不定、更“躁动”。
- $G,F$:PSD、抗噪(无“正负抵消”),适合做稳定的大步更新。
- 驻点附近($g_z\approx 0$)或网络近似线性时:$\mathcal T$ 变小,$G\approx H$。
经验 Fisher(直接用数据标签外积)$\neq$ 真 Fisher;一般也 $\neq$ GGN。实践中要避免用它替代曲率。
6. 读法与实现:如何用它指导优化
6.1 一阶项:方向与步幅
$\Delta L\approx g_z^{\top}J_z\Delta\theta.$
- 若限定 $|\Delta\theta|=\eta$,最陡降方向是 $-J_z^{\top}g_z$(即 $-\nabla_\theta L$)。
- $|J_z^{\top}g_z|$ 大说明“线性项主导”,需要更谨慎的步长/线搜索。
6.2 二阶项:曲率与信任域
$\tfrac12 (J_z\Delta\theta)^{\top}H_L(J_z\Delta\theta)\ \le\ \tfrac12|H_L|\,|J_z\Delta\theta|^2.$
- Sigmoid:$|H_L|\le 1/4$;Softmax:$|H_L|\le 1/2$。
- 结合阻尼/信任域(Tikhonov/Trust-Region),可以安全放大步长(尤其用 $G$ 或 $F$ 时)。
6.3 计算建议(矩阵–向量乘)
优化时常只需 $Gv=J_z^{\top}(H_L(J_z v))$: 「一次 JVP($J_z v$) + 一次 $H_L$ 逐维缩放 + 一次 VJP($J_z^{\top}\cdot$)」即可;用 CG/K-FAC 等可近似解 $(G+\lambda I)\delta=-\nabla L$。
7. 常见问答(把坑提前填平)
- Q:为什么工程上常忽略 $\mathcal T$? A:$\mathcal T$ 的系数是残差 $g_z$;靠近最优时 $p\approx y$,它自然变小;同时 $\mathcal T$ 让 Hessian 不定、难解,忽略后得到 PSD 的 $G/F$,稳定性大幅提升。
- Q:Fisher 与 GGN 什么时候不等价? A:当损失不是 NLL、输出分布不是指数族、或 $z$ 不是自然参数时;此时 $F_R\neq H_L$,只能说两者“相关但不相等”。
- Q:经验 Fisher 能不能当曲率? A:不可靠。它与真 Fisher/GGN 不等价,容易给出误导的缩放;若要二阶,优先用 GGN 或(条件满足时的)真 Fisher。
8. 一页速查(随手可复用)
主方程(记住这一行就够用)
ΔL ≈ gz⊤JzΔθ + 12 (JzΔθ)⊤HL(JzΔθ) + 12 gz⊤Hz[Δθ,Δθ] \boxed{\ \Delta L\ \approx\ g_z^{\top}J_z\Delta\theta\ +\ \tfrac12\,(J_z\Delta\theta)^{\top}H_L(J_z\Delta\theta)\ +\ \tfrac12\,g_z^{\top}\mathcal H_z[\Delta\theta,\Delta\theta]\ }
$\Rightarrow\ \nabla_\theta^2 L=\underbrace{J_z^{\top}H_LJ_z}{\text{GGN/Fisher}}\ +\ \underbrace{\mathcal T}{\text{网络非线性二阶}}$.
Sigmoid-CE:$g_z=p-y$,$H_L=\mathrm{diag}(p(1-p))$,$|H_L|\le 1/4$。
Softmax-CE:$g_z=p-y$,$H_L=\mathrm{diag}(p)-pp^{\top}$,$|H_L|\le 1/2$。
GGN 定义:$G=\mathbb E[J_z^{\top}H_LJ_z]$(PSD)。
Fisher 定义:$F=\mathbb E_x[J_z^{\top}F_R(z)J_z]$;若 NLL + 指数族 + $z$ 为自然参数,则 $F_R=H_L\Rightarrow F\equiv G$。
Hessian 分解:$H=G+\mathcal T$($\mathcal T$ 使 $H$ 可能不定)。
结语
把二阶泰勒展开作为中枢,你已经建立了: 参数扰动 $\Rightarrow$ logit(线性敏感度 + 非线性曲率) $\Rightarrow$ 损失(二阶近似) 的清晰链路; 并理解了 Hessian = GGN + 非线性二阶,以及在常见任务下 Fisher ≡ GGN。 从此,你可以在论文与实现里自如切换“参数空间”的二阶法与“分布空间”的自然梯度视角。