Finsher信息矩阵2

Fisher 信息矩阵的定义

Fisher 信息矩阵定义为

• $Q_x$：输入的分布。理论上是“真实的 $x$ 分布”，实践中通常取经验分布（数据集的均匀分布），因此记作 $x\sim Q_x$ 实际就是“对数据集做平均”。

• 条件模型 $p_\theta(y\mid x)$：给定输入 $x$ 后，标签/输出 $y$ 的模型分布（例如 softmax 分类器）。

• score（得分函数）：

  \[s_\theta(y\mid x):=\nabla_\theta \log p_\theta(y\mid x)\in\mathbb{R}^p.\]

  它衡量“对数似然对参数的即时敏感度”，即增加或减少一个单位的参数值会对对数似然函数产生多大的变化。

• 内层期望 $\mathbb E_{y\mid x}$：在固定 $x$ 的条件下，对 模型分布 $p_\theta(y\mid x)$ 取期望。这是“条件 Fisher”，它度量了在这个 $x$ 上，模型输出分布的“局部不确定度/曲率”。

• 外层期望 $\mathbb E_x$：再对 $x$ 的分布取平均（实践中对数据集求均值），得到“总体 Fisher”。

关键点：Fisher 是关于模型本身的几何量（刻画 KL 的局部曲率），因此 $y$ 的期望必须在模型分布下取（而不是在经验标签上）。如果直接用数据标签外积，得到的是“经验 Fisher”，一般不等于真 Fisher。

信息等式 正则条件下等于“负二阶导的期望”

在正则条件下等于“负二阶导的期望”

证明

(i) score 的期望为 0（固定 $x$） \(\begin{aligned} \mathbb E_{y\mid x}[\,s_\theta(y\mid x)\,] &=\int p_\theta(y\mid x)\,\nabla_\theta\log p_\theta(y\mid x)\,dy \quad(\text{score 的定义）} \\ &=\int \nabla_\theta p_\theta(y\mid x)\,dy \quad(\text{因为 } \nabla_\theta\log p = \tfrac{\nabla_\theta p}{p} \text{将被积函数改写为 $\nabla_\theta p$})\\ &=\nabla_\theta \int p_\theta(y\mid x)\,dy \quad(\text{导数与积分交换, 把导数移出积分})\\ &=\nabla_\theta\, 1 \\ &=0. \end{aligned}\) 在离散情况下有 $$ \begin{aligned} \mathbb E_{y\mid x}[s_\theta(y\mid x)] &=\sum_{y\in\mathcal Y} p_\theta(y\mid x)\,\nabla_\theta\log p_\theta(y\mid x) \

&=\sum_{y\in\mathcal Y}\nabla_\theta p_\theta(y\mid x) \&=\nabla_\theta\sum_{y\in\mathcal Y}p_\theta(y\mid x)
&=\nabla_\theta 1=0. \end{aligned} $$

• 直觉：score 是“对数密度的斜率”。在自己的分布下取平均，相当于问“整体斜率的平均是多少”。但密度已被规范化为 1，整体“朝哪个方向都不能改变总概率”，所以平均斜率为 0。

• 指数族 $r(y\mid z)=h(y)\exp{\eta(z)^\top T(y)-A(\eta(z))}$： 对 $\eta$ 求导得 $s_\eta(y)=T(y)-\nabla_\eta A(\eta)$。在 $y\sim r$ 下， \(\mathbb E[s_\eta]=\mathbb E[T(Y)]-\nabla_\eta A(\eta)=0,\) 因为 $\nabla_\eta A(\eta)=\mathbb E[T(Y)]$。

这与上面的通用证明一致。

(ii) 信息等式（Fisher identity）

对固定 $x$，把 $\log p$ 的 Hessian 展开： \(\nabla^2_\theta \log p =\frac{\nabla^2_\theta p}{p} -\frac{\nabla_\theta p\,\nabla_\theta p^{\top}}{p^2}\) 对 $y\sim p$ 取期望（积分），第一项变为 \(\displaystyle \int \frac{\nabla^2_\theta p}{p}\,p\,dy=\int \nabla^2_\theta p\,dy=\nabla^2_\theta \int p\,dy=0\) 第二项变为 \(-\int \frac{\nabla_\theta p\,\nabla_\theta p^{\top}}{p}\,dy = -\int (\nabla_\theta\log p)(\nabla_\theta\log p)^{\top}p\,dy = -\,\mathbb E[s_\theta s_\theta^{\top}]\) 因此 \(\mathbb E_{y\mid x}\big[\nabla^2_\theta \log p_\theta(y\mid x)\big] = -\,\mathbb E_{y\mid x}\big[s_\theta s_\theta^{\top}\big].\) 再对 $x$ 取外层期望，得到 \(\mathbb E_{y\mid x}\big[\nabla^2_\theta \log p_\theta(y\mid x)\big] = -\,\mathbb E_{y\mid x}\big[s_\theta s_\theta^{\top}\big].\)

正则条件：上面把“导数”移出积分、把“积分”与“导数”交换，需要标准的正则性假设：积分域与参数无关，密度及其导数可积、对 $\theta$ 连续等。

若把损失取为 Negative Log-Likelihood 负对数似然 (NLL) ，$L(y,\theta)=-\log p_\theta(y\mid x)$，则

$\boxed{F(\theta)=\mathbb E_{x}\ \mathbb E_{y\mid x}\big[\nabla_\theta^2 L(y,\theta)\big].}$

另一种视角

1) 生成式/联合视角

若我们有联合模型 $p_\theta(x,y)$，则 \(F(\theta)=\mathbb E_{(x,y)\sim p_\theta(x,y)}\!\big[\nabla_\theta\log p_\theta(x,y)\,\nabla_\theta\log p_\theta(x,y)^{\!\top}\big].\) 分解 $\log p_\theta(x,y)=\log p_\theta(y\mid x)+\log p_\theta(x)$ 并展开，可得

$F= \underbrace{\mathbb E_{x\sim p_\theta(x)}\ \mathbb E_{y\mid x}!\big[s_\theta(y\mid x)s_\theta(y\mid x)^{!\top}\big]}{\text{条件 Fisher}} \;+\;\underbrace{\mathbb E\big[\nabla\log p\theta(x)\nabla\log p_\theta(x)^{!\top}\big]}_{\text{输入边缘的 Fisher}} \;+\;\text{交叉项}.$

• 若 $\theta$ 只作用在 条件分布 $p_\theta(y\mid x)$（判别式建模），且 $p(x)$ 与 $\theta$ 无关，则后一项与交叉项为零，得到

• 在实践中我们通常用经验输入分布 $Q_x$ 近似 $p(x)$，于是得到你第一段的写法：

2) 经典单变量视角

当观测就是 $x$，且 $x\sim p_\theta(x)$（例如参数估计问题里只有一个随机变量），你的第二段写法 \(\boxed{F(\theta)=\mathbb E_{x\sim p_\theta(x)}\big[\nabla_\theta\log p_\theta(x)\,\nabla_\theta\log p_\theta(x)^{\!\top}\big]}\) 正是标准定义。它与上式在“把 $y$ 去掉、只对 $x$ 建模”这一特殊情形下完全一致。

负二阶导形式

在常见正则条件下（导数与积分可交换等）：

$F(\theta)=\mathbb E[\text{score}\,\text{score}^{!\top}] \;=\;-\mathbb E[\nabla_\theta^2\log p_\theta(\cdot)].$

• 条件版：$-\mathbb E_{x\sim Q_x}\ \mathbb E_{y\mid x}[\nabla_\theta^2\log p_\theta(y

  x)]$；

• 无条件版：$-\mathbb E_{x\sim p_\theta(x)}[\nabla_\theta^2\log p_\theta(x)]$。

二者只是期望测度不同（$Q_x$ vs. $p_\theta(x)$）和是否有条件变量（有 $y\mid x$ 或没有）。

一眼辨析：什么时候用哪一个？

• 判别式监督学习（常见分类/回归）：$\theta$ 只参数化 $p_\theta(y\mid x)$，$x$ 的分布与 $\theta$ 无关 ⇒ 用 $\displaystyle F=\mathbb E_{x\sim Q_x}\ \mathbb E_{y\mid x}[s_\theta(y|x)s_\theta(y|x)^{!\top}]$（你的第一段）。
• 生成式建模或单变量参数估计：$\theta$ 直接参数化 $p_\theta(x)$ ⇒ 用 $\displaystyle F=\mathbb E_{x\sim p_\theta(x)}[\nabla\log p_\theta(x)\nabla\log p_\theta(x)^{!\top}]$（你的第二段）。
• 联合建模 $p_\theta(x,y)$：需包含边缘与交叉项；仅当 $\theta$ 不作用于 $p(x)$ 时才退化为条件式。

从 logit 空间 到 概率空间 下 Fisher信息的等价形式

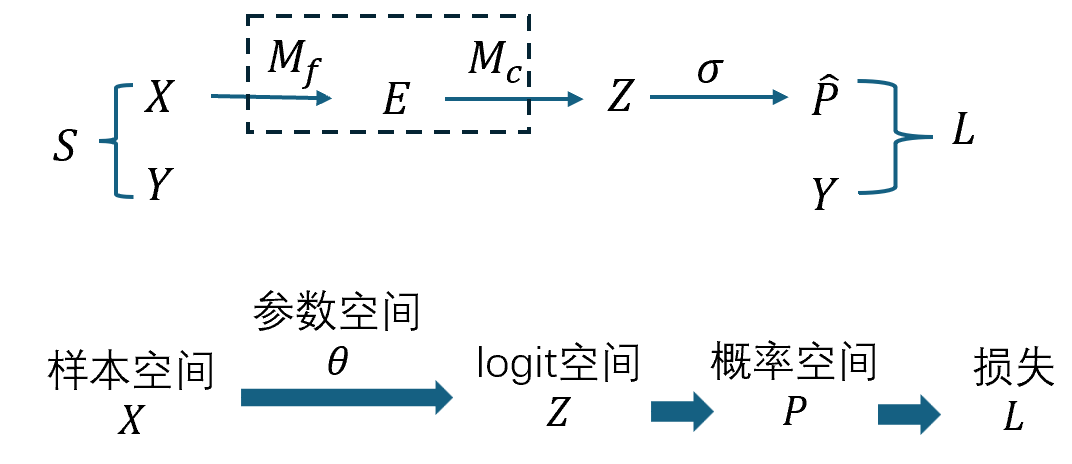
1) 分层模型与两个“score”

• 两层模型：先由网络得到 logit $z=f(x;\theta)\in\mathbb{R}^C$，再用一个输出分布族 $r(y\mid z)$（如 softmax、Bernoulli 等）给出条件概率 $p_\theta(y\mid x)=r!\big(y\mid z=f(x;\theta)\big)$。
• 两个梯度（score）：
  • 参数空间的 score：$s_\theta(y\mid x):=\nabla_\theta \log p_\theta(y\mid x)\in\mathbb{R}^p$；
  • $z$-空间的 score：$s_z(y\mid z):=\nabla_z \log r(y\mid z)\in\mathbb{R}^C$。

链式法则把二者联通： \(\nabla_\theta \log p_\theta(y\mid x) =\Big(\tfrac{\partial z}{\partial\theta}\Big)^{\!\top}\nabla_z \log r(y\mid z) =:J_z^{\top} s_z,\) 其中 $J_z:=\partial z/\partial\theta\in\mathbb{R}^{C\times p}$ 是 logit 对参数的雅可比。

维度核对：$J_z^{\top}s_z\in\mathbb{R}^{p}$，与参数维度一致。

2) 代回 Fisher 的定义，并用“塔式法则”整理

条件 Fisher（监督学习常用）定义为 \(F(\theta)=\mathbb{E}_{x}\ \mathbb{E}_{y\sim p_\theta(\cdot\mid x)} \big[\,s_\theta(y\mid x)\,s_\theta(y\mid x)^{\!\top}\big].\) 把 $s_\theta=J_z^{\top}s_z$ 代入：

\(\begin{aligned} F(\theta) &=\mathbb{E}_{x}\ \mathbb{E}_{y\mid x} \big[J_z^{\top}s_z\,s_z^{\top}J_z\big] \\ &=\mathbb{E}_{x}\Big[J_z^{\top}\underbrace{\mathbb{E}_{y\mid x}[\,s_z s_z^{\top}\,]}_{=:F_R(z)}\,J_z\Big] = \boxed{\ \mathbb{E}_{x}\big[J_z^{\top}F_R(z)\,J_z\big]\ }. \end{aligned}\) 这里用到两点：

• (i) 条件期望的塔式法则：$\mathbb{E}{x}\mathbb{E}{y\mid x}[\cdot]=\mathbb{E}_{x,y}[\cdot]$。
• (ii) 给定 $x$ 时，$J_z=J_z(x,\theta)$ 与 $z$ 只依赖 $x,\theta$，与 $y$ 无关，可从内层 $\mathbb{E}_{y\mid x}$ 中“提出去”。

定义

是输出分布族在 $z$-空间的 Fisher。

维度核对：$F_R(z)\in\mathbb{R}^{C\times C}$；$J_z^{\top}F_R(z)J_z\in\mathbb{R}^{p\times p}$，与 $F(\theta)$ 维度一致。

3) 这一步“在说什么”？——pullback（拉回）直觉

• $F_R(z)$ 是概率模型 $r(y\mid z)$ 在 logit 空间上的“局部度量”（衡量在当前 $z$ 处，分布对 $z$ 的微小扰动有多敏感）。
• $J_z$ 是从参数空间到 logit 空间的线性化映射（微分）。
• 于是 $(\Delta\theta)^{!\top}F(\theta)\Delta\theta = \mathbb{E}_x\big[(J_z\Delta\theta)^{!\top}F_R(z)(J_z\Delta\theta)\big]$： 先把参数扰动 $\Delta\theta$ 映到 logit 扰动 $J_z\Delta\theta$，再用 $F_R$ 在 $z$-空间测量其“长度”，最后对 $x$ 取平均。 这正是微分几何里把一个度量从目标空间拉回（pullback）到参数空间的标准形式。

指数族 + 自然参数条件下，$z$-空间的 Fisher 等价于 损失 $L(y,z)$ 对 $z$ 的 二阶 Hessian矩阵

在 Negative Log-Likelihood负对数似然+ 指数族且 $z$ 为自然参数 的条件下，$F_R(z)=\nabla_z^2 L(y,z)=:H_L(z)$，于是 $F(\theta)=\mathbb{E}_x[J_z^{\top}H_L(z)J_z]\ \equiv\ \text{GGN},$ 把分布空间的度量与你在二阶泰勒中出现的 GGN 二次型完全对齐。

A. 为何 $F_R(z)=H_L(z)$（关键等价）

A1. 指数族与 NLL 的结构

令输出分布为指数族，以 $z\in\mathbb R^C$ 为自然参数：

• 负对数似然（逐样本损失）： \(L(y,z)=-\log r(y\mid z)=A(z)-z^{\top}T(y)-\log h(y).\)

• 一阶：$\displaystyle \nabla_z L(y,z)=\nabla_z A(z)-T(y)=\mu(z)-T(y)$， 其中 $\mu(z):=\nabla_z A(z)=\mathbb E_{r(\cdot\mid z)}[T(Y)]$。

• 二阶：$\displaystyle \nabla_z^2 L(y,z)=\nabla_z^2 A(z)=\mathrm{Cov}_{r(\cdot\mid z)}[T(Y)]$，与 $y$ 无关（只依赖 $z$）。

A2. $z$-空间 Fisher 与 NLL Hessian 的一致

$z$-空间的 Fisher 定义为

$F_R(z)=\mathbb E_{y\sim r(\cdot\mid z)}!\big[\nabla_z\log r(y\mid z)\,\nabla_z\log r(y\mid z)^{!\top}\big].$

而 $\nabla_z\log r(y\mid z)=T(y)-\mu(z)=-(\nabla_z L)$。取期望得

因此在该设定下，Fisher（分布几何）= NLL 的 $z$-Hessian（损失曲率）。

A3. 拉回到参数空间：Fisher ≡ GGN

条件 Fisher 的“拉回”形式是

这与上面“负二阶导的期望”表述是完全一致的。

将 $F_R(z)$ 换成 $H_L(z)$ 即得

$\boxed{F(\theta)=\mathbb E_x\big[J_z^{\top}H_L(z)J_z\big]\ \equiv\ \text{GGN}.}$

这恰好是你在二阶泰勒展开里的“GGN/Fisher 二次型”：

$(J_z\Delta\theta)^{!\top}H_L(z)\,(J_z\Delta\theta).$

故而分布空间的度量（KL 的二次近似）*与*参数空间的 GGN 二次型完全对齐。

典型实例

• Sigmoid + Bernoulli-CE：$H_L(z)=\mathrm{diag}(p\odot(1-p))$。
• Softmax + 多类 CE：$H_L(z)=\mathrm{diag}(p)-pp^{\top}$。
• 固定方差高斯 + MSE：$H_L(z)=\sigma^{-2}I$。 三者均满足“指数族 + 自然参数”，因而 Fisher ≡ GGN。

何时不再等价？ 若损失不是 NLL，或分布非指数族，或 $z$ 不是自然参数（例如把 $z$ 经过非线性再当“参数”），一般 $F_R\neq H_L$，于是 Fisher $\neq$ GGN。

关系总结

1. 关于“Fisher 定义在权重空间、等于负二阶导期望”

   对监督学习的条件模型 $p_\theta(y\mid x)$，真 Fisher 定义为

   \[F(\theta)=\mathbb E_{x}\ \mathbb E_{y\sim p_\theta(\cdot\mid x)} \big[\nabla_\theta\log p_\theta(y\mid x)\,\nabla_\theta\log p_\theta(y\mid x)^\top\big].\]

   在常见的正则条件下（支集不随 $\theta$ 变、可微且可交换导数与积分），有“信息等式”：

   \[F(\theta)= -\,\mathbb E_{x}\ \mathbb E_{y\mid x}\big[\nabla_\theta^2\log p_\theta(y\mid x)\big].\]

   若训练损失取 NLL（$L=-\log p_\theta(y\mid x)$），则再写成

   \[F(\theta)=\mathbb E_{x}\ \mathbb E_{y\mid x}\big[\nabla_\theta^2 L(y,\theta)\big].\]

   注意：这里的期望是在模型分布下取的；直接用真实标签做外积得到的是经验 Fisher，一般不等于真 Fisher。

2. 关于“$z$-空间 Fisher 与 $L(y,z)$ 的 Hessian 等价，等价于 GGN”

   • 在 NLL + 指数族且 $z$ 为自然参数 时，有

     \[F_R(z)=\mathbb E_{y\mid z}[\nabla_z\log r\,\nabla_z\log r^\top] = \nabla_z^2 L(y,z)=:H_L(z),\]

     因而参数空间的 Fisher

     \[F(\theta)=\mathbb E_{x}\big[J_z^\top F_R(z)\,J_z\big] =\mathbb E_{x}\big[J_z^\top H_L(z) J_z\big]\ \equiv\ \text{GGN}.\]

     这时 Fisher 与你二阶泰勒展开里的 GGN 二次型完全对齐。

   • 若不满足上述条件（损失不是 NLL、分布非指数族、或 $z$ 不是自然参数），一般只有

     \[F(\theta)=\mathbb E_x\big[J_z^\top\,\underbrace{\mathbb E_{y\mid x}[H_L(z,y)]}_{\text{对 }y\text{ 的期望}}\,J_z\big],\]

     而不能简化为 $\mathbb E_x[J_z^\top H_L(z)J_z]$，故 Fisher $\neq$ GGN。

一句话总结

• 广义真相：在 正则条件下，$\displaystyle F=-\mathbb E[\nabla_\theta^2\log p_\theta]$。
• 更强等价：若再加“指数族 + 自然参数”，则 $F_R(z)=H_L(z)$，于是 $\displaystyle F=\mathbb E_x[J_z^{\top}H_LJ_z]\equiv\text{GGN}$，这与二阶泰勒中的 GGN 二次型逐样本对齐。

B. 实现：如何在不显式构造矩阵的前提下用到 $F$（或 GGN）

B1. 只需做 $v\mapsto Fv$ 的矩阵–向量乘（MvP）

对任意向量 $v\in\mathbb R^{p}$：

$Fv=\mathbb E_x\big[J_z^{\top}H_L(z)\,J_z v\big].$

小批量近似下，单次 MvP 的计算步骤：

1. JVP：$a \leftarrow J_z v$\ $\in\mathbb R^{C}$（前向模式/一次“正向增量传播”）。
2. z-空间缩放：$b \leftarrow H_L(z)\,a$\（逐样本、逐维或协方差型缩放）。
   • Sigmoid：$b_k = p_k(1-p_k)\,a_k$。
   • Softmax：$b = \mathrm{diag}(p)a - p\,(p^{\top}a) = a - p\,(p^{\top}a)$（数值上只需内积一次）。
   • MSE/高斯：$b=\sigma^{-2}a$。
3. VJP：返回 $Fv \leftarrow J_z^{\top} b$\（一次反向传播/向量–雅可比积）。

代价：约等于“一次 JVP + 一次 VJP”，即“$\sim$ 2 次反向传播”的计算量；无需显式形成 $J_z,\,H_L,\,F$。

B2. 用 MvP 解 $(F+\lambda I)\delta=-g$

• CG（共轭梯度）：只要能提供 MvP，就能用 CG 迭代近似解该线性系统，得到“自然梯度/二阶步” $\delta\approx-(F+\lambda I)^{-1}g$。
• K-FAC：把 $F$ 的层内块近似为 Kronecker 分解（激活二阶矩 $\otimes$ 误差二阶矩），以闭式或近闭式的方式近似 $(F+\lambda I)^{-1}$ 应用到梯度上；适合大网络、大 batch。
• 阻尼 $\lambda$：保证可逆、控制步幅（Tikhonov/信任域），与“限制 KL 步长”等价/相近。

B3. 真 Fisher vs. 经验 Fisher

• 真 Fisher：$\mathbb E_{y\sim p_\theta(y\mid x)}[\cdot]$ —— 在模型分布下取期望（几何量）。
• 经验 Fisher（EF）：直接用数据标签 $(x,y)$ 做外积 —— 在经验分布下取期望。 结论：EF 一般 $\neq F$，且通常 $\neq$ GGN；只有在模型“完全拟合且正确指定”的理想极限附近才可能近似。工程上若用 EF 代替曲率，可能出现缩放失真与收敛不稳。

C. 一句话总结

当损失为 NLL 且输出分布为指数族（以 $z$ 为自然参数）时，

$F_R(z)=H_L(z)\quad\Rightarrow\quad F(\theta)=\mathbb E_x[J_z^{\top}H_L(z)J_z]\equiv \text{GGN}.$

这使得分布几何（Fisher/KL）*与*参数二阶近似（GGN）*在你泰勒展开中的二次型*完美对齐；实现上只需 JVP→z-缩放→VJP 的三步 MvP，就能把 CG/K-FAC 等二阶/自然梯度方法落到实际训练中。